Закон Вебера-Фехнера | Digital Music Academy
Зачем такие сложности?
Одна из причин применения децибелов, т.е. относительной логарифмической шкалы громкости — психофизиологическая («живая природа живёт по логарифму»). Характер восприятия человеком и животными многих физических и биологических процессов таков, что изменения воспринимаются пропорционально именно логарифму интенсивности воздействия. В частности, минимальное заметное изменение громкости приблизительно соответствует 1 дБ.
Закон Вебера-Фехнера
Эмпирический психофизиологический закон, согласно которому интенсивность ощущения пропорциональна логарифму интенсивности раздражителя.
В ряде экспериментов, начиная с 1834 года, немецкий психофизиолог Эрнст Вебер показал, что новый раздражитель, чтобы отличаться по ощущениям от предыдущего, должен отличаться от исходного на величину, пропорциональную исходному раздражителю.
где:
S — значение интенсивности раздражителя;
S0 — нижнее граничное значение интенсивности раздражителя; если S < S0, раздражитель совсем не ощущается;
k — константа, зависящая от субъекта ощущения.
Так, люстра, в которой 8 лампочек, кажется нам настолько же ярче люстры из 4 лампочек, насколько люстра из 4 лампочек ярче люстры из 2 лампочек. То есть количество лампочек должно увеличиваться в одинаковое число раз, чтобы нам казалось, что прирост яркости постоянен.
И наоборот, если абсолютный прирост яркости (разница в яркости «после» и «до») постоянен, то нам будет казаться, что абсолютный прирост уменьшается по мере роста самого значения яркости.
Например, если добавить одну лампочку к люстре из двух лампочек, то кажущийся прирост в яркости будет значительным.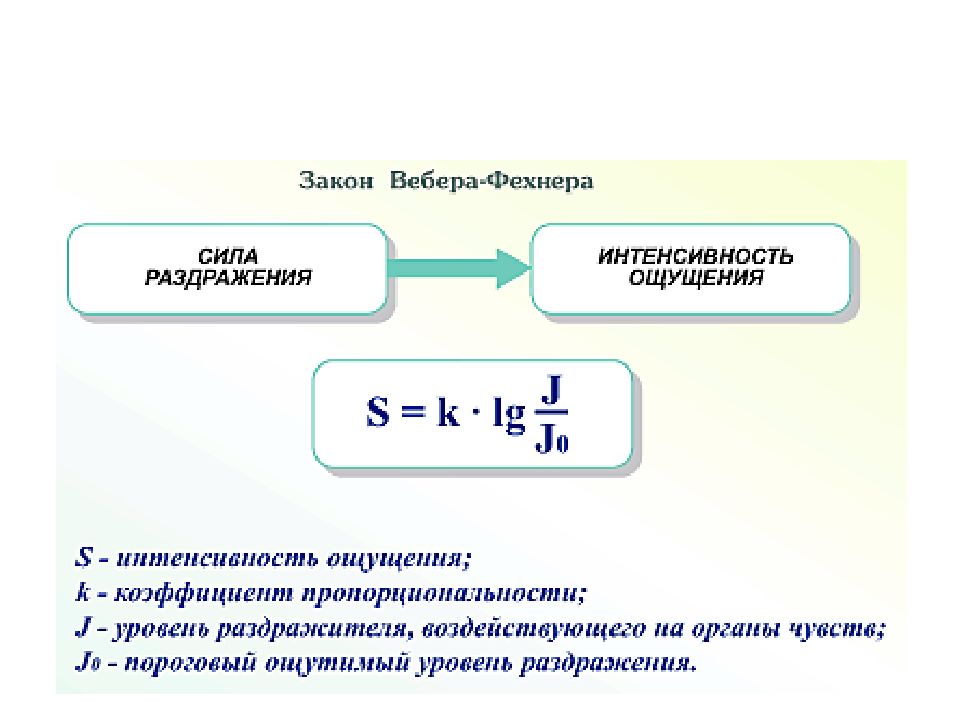 Если же добавить одну лампочку к люстре из 12 лампочек, то мы практически не заметим прироста яркости.
Если же добавить одну лампочку к люстре из 12 лампочек, то мы практически не заметим прироста яркости.
Можно сказать и так: отношение минимального приращения силы раздражителя, впервые вызывающего новые ощущения, к исходной величине раздражителя есть величина постоянная.
(В XX веке Стенли Смитом Стивенсом была доказана ограниченность закона Вебера—Фехнера, справедливого лишь для некоторых типов ощущений. В целом же зависимость носит характер степенной функции с различными показателями степени для каждого рода условий (закон Стивенса).)
Закон Вебера — Фехнера — Психологос
Густав Теодор Фехнер
Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула.
В ряде экспериментов, начиная с 1834 года, Э. Вебер показал, что новый раздражитель, чтобы отличаться по ощущениям от предыдущего, должен отличаться от исходного на величину, пропорциональную исходному раздражителю. Так, чтобы два предмета воспринимались как различные по весу, их вес должен различаться на 1/30, для различения яркости двух источников света необходимо, чтобы их яркость отличалась на 1/100 и т. д.
Вебер показал, что новый раздражитель, чтобы отличаться по ощущениям от предыдущего, должен отличаться от исходного на величину, пропорциональную исходному раздражителю. Так, чтобы два предмета воспринимались как различные по весу, их вес должен различаться на 1/30, для различения яркости двух источников света необходимо, чтобы их яркость отличалась на 1/100 и т. д.
На основе этих наблюдений Г. Фехнер в 1860 году сформулировал «основной психофизический закон», по которому сила ощущения p пропорциональна логарифму интенсивности раздражителя S:
p=k*log{S}\{S_0}
где S_0 — граничное значение интенсивности раздражителя: если S<S_0, раздражитель совсем не ощущается.
Эрнст Генрих Вебер
Так, люстра в которой 8 лампочек, кажется нам настолько же ярче люстры из 4-х лампочек, насколько люстра из 4-х лампочек ярче люстры из 2-х лампочек. То есть, количество лампочек должно увеличиваться в разы, чтобы нам казалось, что прирост яркости постоянен. И наоборот, если прирост яркости постоянен, нам будет казаться, что он уменьшается. Например, если добавить одну лампочку к люстре из 12 лампочек, то мы практически не заметим прироста яркости. В то же время, одна лампочка, добавленная к люстре из двух лампочек, даёт значительный кажущийся прирост яркости.
То есть, количество лампочек должно увеличиваться в разы, чтобы нам казалось, что прирост яркости постоянен. И наоборот, если прирост яркости постоянен, нам будет казаться, что он уменьшается. Например, если добавить одну лампочку к люстре из 12 лампочек, то мы практически не заметим прироста яркости. В то же время, одна лампочка, добавленная к люстре из двух лампочек, даёт значительный кажущийся прирост яркости.
Закон Вебера — Фехнера можно объяснить тем, что константы скорости химических реакций проходящих при рецептировании нелинейно зависят от концентрации химических посредников физических раздражителей или собственно химических раздражителей.
Основной психофизический закон Вебера-Фехнера
Сущность закона Вебера-Фехнера
Определение 1
Закон Вебера-Фехнера — это психофизический закон, суть которого состоит в том, что интенсивность ощущения прямо пропорциональна логарифму интенсивности раздражителя
В психофизике закон Вебера-Фехнера сочетает в себе два различных закона человеческого восприятия.
Эрнст Генрих Вебер (1795-1878) был одним из первых людей, который начал изучение человеческой реакции на физический стимул в количественном выражении. Закон Вебера гласит, что заметная разница между двумя стимулами пропорциональна величине стимулов (и чувствительности субъекта), то есть если вы чувствуете изменение веса на 0,5 фунта у гантели весом 5 фунтов, то у десятифунтовой гантели вы почувствуете прибавление 1 фунта.
Готовые работы на аналогичную тему
Густав Теодор Фехнер (1801–1887) позже использовал выводы Вебера для построения психофизической шкалы, в которой он описал взаимосвязь между физической величиной стимула и его субъективно воспринимаемой интенсивностью. Закон Фехнера (иначе называемый шкалой Фехнера) гласит, что субъективное ощущение пропорционально логарифму интенсивности стимула. Масштабирование Фехнера математически формализовано. На самом деле человеческое восприятие зрения и звука работает следующим образом: воспринимаемая громкость (яркость) пропорциональна логарифму фактической интенсивности, измеренной точным техническим инструментом.
Замечание 1
Некоторые авторы используют термин «закон Вебера-Фехнера» для обозначения закона Вебера, а другие используют его для закона Фехнера. Использование термина «закон Вебера-Фехнера» было раскритиковано Эвальдом Герингом как неправильное употребление.
Вывод закона Фехнера для восприятия веса
Вебер обнаружил, что заметна разница между двумя весами, которая приблизительно пропорциональна им. Таким образом, если только вес 105 г (а не 104 г или 104,9 г) можно отличить от веса 100 г, дифференциальный порог равен 5 г. Если масса образца удваивается, дифференциальный порог также удваивается до 10 г так, что можно отличить 210 г от 200 г. В этом примере вес (любой вес), по-видимому, должен увеличиться на 5%, чтобы кто-то мог надежно обнаружить прибавление, и это минимально необходимое дробное увеличение (5/100 от исходного веса) называется «Фракция Вебера» для выявления изменений в весе. Другие задачи различения, такие как обнаружение изменений яркости, высоты тона (частоты чистого тона) или длины линии, отображаемой на экране, могут иметь разные дроби Вебера.
Этот вид отношений может быть описан дифференциальным уравнением:
$dp = k • dS / S$,
где:
- $dp$ — дифференциальное изменение восприятия,
- $S$ — мгновенный стимул.
Параметр $k$ должен быть оценен с использованием экспериментальных данных.
Связь между стимулом и восприятием логарифмическая . Это логарифмическое соотношение означает, что если стимул изменяется как геометрическая прогрессия (т.е. умножается на фиксированный коэффициент), соответствующее восприятие изменяется в арифметической прогрессии (т.е. в постоянных количествах добавок). Например, если стимул утроен по силе (то есть 3 x 1), соответствующее восприятие может быть в два раза сильнее его первоначального значения (то есть 1 + 1). Если стимул снова утроится по силе (т.е. 3 x 3 x 1), соответствующее восприятие будет в три раза сильнее его первоначального значения (т.е. 1 + 1 + 1). Следовательно, при умножении силы стимула, сила восприятия только прибавляется.
Недостатки закона Вебера-Фехнера
Фехнер не проводил никаких экспериментов о том, как воспринимаемая тяжесть увеличивается с массой раздражителя. Вместо этого он предположил, что все они субъективно равны, и математически утверждал, что это приведет к логарифмической связи между интенсивностью стимула и ощущением. Эти предположения были подвергнуты сомнению. В настоящее время большинство исследователей признают, что степенной закон является более реалистичным отношением или что логарифмическая функция является лишь одной из возможных функций.
Другие способы восприятия обеспечивают лишь смешанную поддержку как закона Вебера, так и закона Фехнера. Так Закон Вебера не совсем верен для громкости. Это справедливо для звуков более высокой интенсивностей, но не для более низких амплитуд.
Первая демонстрация явлений была представлена Рисом в 1928 году в Physical Review. Это отклонение от закона Вебера известно как «ближний промах» закона Вебера. Этот термин был придуман Макгиллом и Голдбергом в их статье «Восприятие и психофизика» 1968 года. Их исследование состояло в различении интенсивности в чистых тонах. Дальнейшие исследования показали, что ближний промах наблюдается и при шумовых раздражителях.
Их исследование состояло в различении интенсивности в чистых тонах. Дальнейшие исследования показали, что ближний промах наблюдается и при шумовых раздражителях.
Глаз воспринимает изменение яркости в умеренном диапазоне приблизительно логарифмически, а звездная величина измеряется в логарифмическом масштабе. Эта шкала величин была изобретена древнегреческим астрономом Гиппархом примерно в 150 г. до н.э. Он оценил звезды, которые мог видеть, с точки зрения их яркости, от 1, представляющей самые яркие светила, до 6, представляющей самые слабые.
Применение закона
Этот закон применяется в областях оценки величины, таких как работа с большими масштабами и оценка расстояний. Он также может сыграть роль в объяснении того, почему потребители отказываются ходить по магазинам, чтобы сэкономить небольшой процент на крупной покупке, но будут ходить по магазинам, чтобы сэкономить большой процент на небольшой покупке, которая представляет собой гораздо меньшую абсолютную сумму в долларах.
Закон Вебера-Фехнера на примере лампочек и бумажек
«Интенсивность ощущения пропорциональна логарифму интенсивности стимула» — так звучит формулировка закона Вебера-Фехнера. Сразу видно, умные слова, глубокий смысл в них и ценная информация… Понимать бы еще, что все это значит! А как раз в этом мы сейчас и разберемся… Итак, начнем по порядку. Во-первых, нужно разобраться с тем, чей это закон и при каких обстоятельствах он появился в уме своего создателя.
Кто такой «Вебер-Фехнер»?
Для начала, немного изучим того человека, который является непосредственно создателем закона Вебера-Фехнера. И сразу же поправочка… Их два. Нет, не закона, а человека.
Эрнст Генрих Вебер — это психофизиолог и анатом из Германии и брат известного физика Вильгельма Эдуарда Вебера, в честь которого даже была названа единица измерения магнитного потока.
Густав Теодор Фехнер — психолог из Германии, а также основоположник психофизиологии и психофизики.
История экспериментов и сущность закона Вебера-Фехнера
История зарождения этого закона началась еще в далеком одна тысяча восемьсот тридцать четвертом году, когда начали проводиться первые эксперименты Эрнста Вебера. Как раз в них ученый показал, что ощущения от нового раздражителя будут отличительны от раздражений, получаемых новым раздражителем в том случае, если интенсивность нового будет отличаться от интенсивности старого на величину, которая будет пропорциональна интенсивности предыдущего раздражителя. А уже, основываясь на этих экспериментах, Густав Фехнер сформулировал закон, о котором говорилось в данной статье выше. Закон Вебера-Фехнера в психологии также оставил большой след.
Как раз в них ученый показал, что ощущения от нового раздражителя будут отличительны от раздражений, получаемых новым раздражителем в том случае, если интенсивность нового будет отличаться от интенсивности старого на величину, которая будет пропорциональна интенсивности предыдущего раздражителя. А уже, основываясь на этих экспериментах, Густав Фехнер сформулировал закон, о котором говорилось в данной статье выше. Закон Вебера-Фехнера в психологии также оставил большой след.
Формула закона
Ранее рассмотренная формулировка закона Вебера-Фехнера приобрела даже свою особую формулу: p=k*log{S}{S_0} — сила ощущения пропорциональна логарифму интенсивности раздражителя.
В этой формуле S_0 — будет являться значением, которое отражает интенсивность раздражителя.
Расшифровка формулировки закона
Для того чтобы понять эти слова лучше, представьте перед собой люстру, которая имеет восемь лампочек и все они включены. Также представьте люстры с четырьмя включенными лампочками и третью люстру со всего лишь двумя включенными лампочками. Согласитесь, первая люстра настолько же ярче второй, насколько вторая ярче третьей… Для того чтобы у нас возникало ощущение постоянного прироста яркости, количества лампочек в люстре должно будет увеличиваться в разы. И в тот же момент, наоборот! Нам может казаться, что прирост яркости уменьшается в тот момент, когда увеличивается количество включенных лампочек в люстре. Чтобы понять это, представьте, словно перед вами находится люстра с двенадцатью включенными лампочками. А после этого представьте люстру, в которой будут включены тринадцать лампочек. Вы ведь тоже практически не замечаете, что яркость увеличилась? Но если бы мы добавили одну лампочку к той люстре, что состояла из двух, то не было бы места вопросу об увеличении яркости света, исходящего от люстры.
Согласитесь, первая люстра настолько же ярче второй, насколько вторая ярче третьей… Для того чтобы у нас возникало ощущение постоянного прироста яркости, количества лампочек в люстре должно будет увеличиваться в разы. И в тот же момент, наоборот! Нам может казаться, что прирост яркости уменьшается в тот момент, когда увеличивается количество включенных лампочек в люстре. Чтобы понять это, представьте, словно перед вами находится люстра с двенадцатью включенными лампочками. А после этого представьте люстру, в которой будут включены тринадцать лампочек. Вы ведь тоже практически не замечаете, что яркость увеличилась? Но если бы мы добавили одну лампочку к той люстре, что состояла из двух, то не было бы места вопросу об увеличении яркости света, исходящего от люстры.
Итак, были подтверждены наблюдения, что человек способен чувствовать совсем не любые раздражения, а только те, которые обладают достаточно большой интенсивностью.
Пороги чувствительности в законе Вебера-Фехнера
Было обнаружено, что для того, чтобы человека почувствовал на себе действие того или иного раздражителя, его интенсивность должна будет достичь определенного уровня. Нижний порог чувствительности — это слабое и едва заметно воздействие интенсивности.
Нижний порог чувствительности — это слабое и едва заметно воздействие интенсивности.
Логичным и правильным будет предположение о том, что помимо нижнего порога чувствительности существует также и верхний порог. Это тот уровень воздействия, после увеличения которого чувства уже не способны делаться сильнее.
Любое из воздействий на себя человек может чувствовать исключительно в промежутке между двумя этими состояниями. Именно из-за этого их называют внешними порогами чувствительности (или внешними порогами ощущения).
Стоит упомянуть и о том, что невозможно существовать параллелизму между интенсивностями чувствительности и раздражения, даже в межпороговом промежутке.
Расшифровка порогов чувствительности
Приведем тому пример… А для этого представьте, словно в руки вы берете какую-либо сумку, которая обладает некоторым весом. Теперь положите в вашу сумку бумажный лист. На самом деле, теперь вес сумки увеличился. Но вы этого не чувствуете, хотя эта разница находится в промежутки между этими двумя порогами чувствительности.
В данном случае можно рассуждать о том, что увеличение раздражения, на самом деле, слишком мало. Порогом различения называется та величина, на которую увеличивается раздражение. Теперь можно сделать вывод о том, что раздражение со слишком малым порогом различения является допороговым, а со слишком сильным, наоборот, запороговым. Но так же уровень таких показателей зависит от чувствительности различения. Чем выше чувствительность к ней, тем ниже порог различения.
Именно Вебер был первым человеком, который обратил внимание на то, что порог различения может быть абсолютным и релятивным. Очень важно отличать первый от второго. Абсолютным порогом является тот прирост интенсивности раздражения, который необходим, чтобы достичь порога различения. Снова приведем пример.
Чтобы почувствовать изменение двух тысячи граммового веса, к нему следует добавить еще двести грамм веса. Эта величина и является абсолютным порогом чувствительности. Но в случае, если вес нашего раздражителя составляет четыре тысячи грамм, этих двух сот грамм нам окажется недостаточно для того, чтобы ощутить на себе разницу.
Если эти же двести грамм представить числом, выражающим отношение между добавочным раздражением и основным раздражением, то это окажется релятивным порогом различения.
Такова вся сущность закона Вебера-Фехнера.
Закон Вебера — Фехнера
Закон Вебера — Фехнера представляет собой важнейшее открытие в области психофизики, который позволяет охарактеризовать то, что, казалось бы, не способно поддаваться какой бы то ни было характеристике, а именно, ощущения человека.
Основной психофизический закон Вебера — Фехнера
Прежде всего, рассмотрим самые важные составляющие этого выражения. Закон Вебера — Фехнера гласит, что интенсивность ощущения человека пропорциональна логарифму интенсивности стимула. Что и говорить, с первого раза такая формулировка закона Вебера – Фехнера звучит пугающе, но на самом деле, все довольно просто.
Еще в 19 веке ученый Э. Вебер сумел показать при помощи нескольких экспериментов, что каждый новый раздражитель, чтобы человек имел возможность воспринимать его как отличающийся от предыдущего, должен иметь разницу с предыдущим вариантном на величину, которая пропорциональна исходному раздражителю.
В качестве простейшего примера данного утверждения можно привести любые два предмета, имеющие некую массу. Чтобы человек мог воспринимать их как отличные по весу, второй должен отличаться на 1/30.
Другой пример можно привести на освещении. Чтобы человек увидел разницу в свете двух люстр, их яркость должна отличаться на 1/100. То есть люстра из 12 лампочек будет слабо отличаться от той, к которой прибавили всего лишь одну, а люстра из одной лампочки, к которой прибавили еще одну, будет давать ощутимо больше света. Не смотря на то, что прибавляется и в том, и в другом случае лишь одна лампочка, восприниматься разница в освещении будет по-разному, поскольку важно именно соотношение исходного раздражители и того, который является последующим.
Закон Вебера – Фехнера: формулаФормулировка, которую мы рассмотрели выше, подкрепляется особой формулой, которая выражает действие психофизического закона Вебера – Фехнера. В 1860 году Фехнер сумел сформулировать закон, который гласит, что сила ощущения p пропорциональна логарифму интенсивности раздражителя S:
p=k*log{S}\{S_0}
где S_0 — значение, отражающее интенсивность раздражителя: если S
Для понимания этого закона особенно важным является понятие так называемого порога, установленное в процессе психофизических исследований.
Пороги ощущений закон Вебера — Фехнера
Впоследствии было выяснено, что существующей интенсивности раздражения требуется достижение некоего конкретного уровня, чтобы человек имел возможность почувствовать его воздействие. Такое слабое воздействие, которое дает еле заметное ощущение, называют нижним порогом ощущения.
Существует и такой уровень воздействия, после увеличение которого ощущения уже не способны усиливаться. В этом случае речь идет о верхнем пороге ощущения. Любого рода воздействие человек ощущает исключительно и интервале между этими двумя показателями, которые благодаря этому именуют внешними порогами ощущения.
Нельзя не сказать и о том, что параллелизма в полном смысле этого слова между интенсивностями ощущения и раздражения нет и быть не может даже в межпороговом интервале. Это легко подтвердить примером: представьте, что вы взяли в руки сумку, и она, разумеется, имеет некий вес. После этого мы положим в сумку лист бумаги. Фактически вес сумки теперь увеличен, однако человек не ощутит такой разницы, не взирая на то, что она лежит в зоне между двумя порогами.
В этом случае речь идет о том, что прирост раздражения слишком слабый. Величина, на которую раздражение увеличивается, принято называть порогом различения. Отсюда следует, что раздражение со слишком малой различительной интенсивностью является допороговым, а со слишком сильной – запороговым. При этом уровень этих показателей зависит и от чувствительности в отношении различения – если чувствительность к различению выше, то порог различения, соответственно, ниже.
1.8. Закон Вебера-Фехнера
1 |
1.8. Характеристики анализаторов. |
|
|
|
Закон Вебера-Фехнера |
Основное свойство анализатора — чувствительность рецептора, то есть его способность воспринимать раздражение.
Различают следующие характеристики анализаторов:
1.Верхний и нижний абсолютные пороги чувствительности.
2.Диапазон чувствительности, расположенный между порогами.
3.Дифференциальный порог чувствительности, то есть минимальная разность между интенсивностями раздражителя, способная вызвать едва заметное различие ощущений.
4.Латентный период — время от начала воздействия раздражителя до появления ощущения.
2
Дробь Вебера
Степень восприятия оценивается относительной величиной интенсивности раздражителя, что характеризуется дробью
Вебера:
I const I0
где ΔI — приращение интенсивности раздражителя; I0 — первоначальная интенсивность.
Например, если горит 10 ламп, то добавление одной вызывает едва заметное изменение освещённости. Однако, если зажжено 100 ламп, то чтобы получить изменение освещённости, надо добавить уже 10 ламп. Считая, что количество ламп пропорционально силе света, это рассуждение можно выразить дробью:
1/10=10/100=100/1000=0,1. Анв
3 |
Психофизиологический закон |
|
Вебера-Фехнера |
Установлено, что величина ощущения изменяется медленнее, чем сила раздражителя. Закон Вебера-Фехнера связывает уровень ощущения L и силу (интенсивность) раздражителя I. Формулировка закона:
Закон Вебера-Фехнера связывает уровень ощущения L и силу (интенсивность) раздражителя I. Формулировка закона:
Уровень ощущения L пропорционален логарифму относительной величины интенсивности I раздражителя.
L K lg I C , I0
где I0 — интенсивность на нижнем пороге чувствительности; К и С — некоторые константы.
Анв
5
Выводы из закона Вебера-Фехнера
Из рисунка 13 видно, что при малых значениях аргумента крутизна подъёма логарифмической кривой велика, а по мере увеличения аргумента степень крутизны уменьшается.
1 В диапазоне работы анализатора степень чувствительности определяется относительной величиной то есть, отношением
интенсивности к интенсивности на нижнем пороге чувствительности.
2 Чувствительность анализатора возрастает при слабых раздражителях и автоматически загрубляется при действии мощных раздражителей; этим обеспечивается самозащита
анализатора и человека.
Закон Вебера-Фехнера только в первом приближении моделирует сложный физиологический процесс ощущений.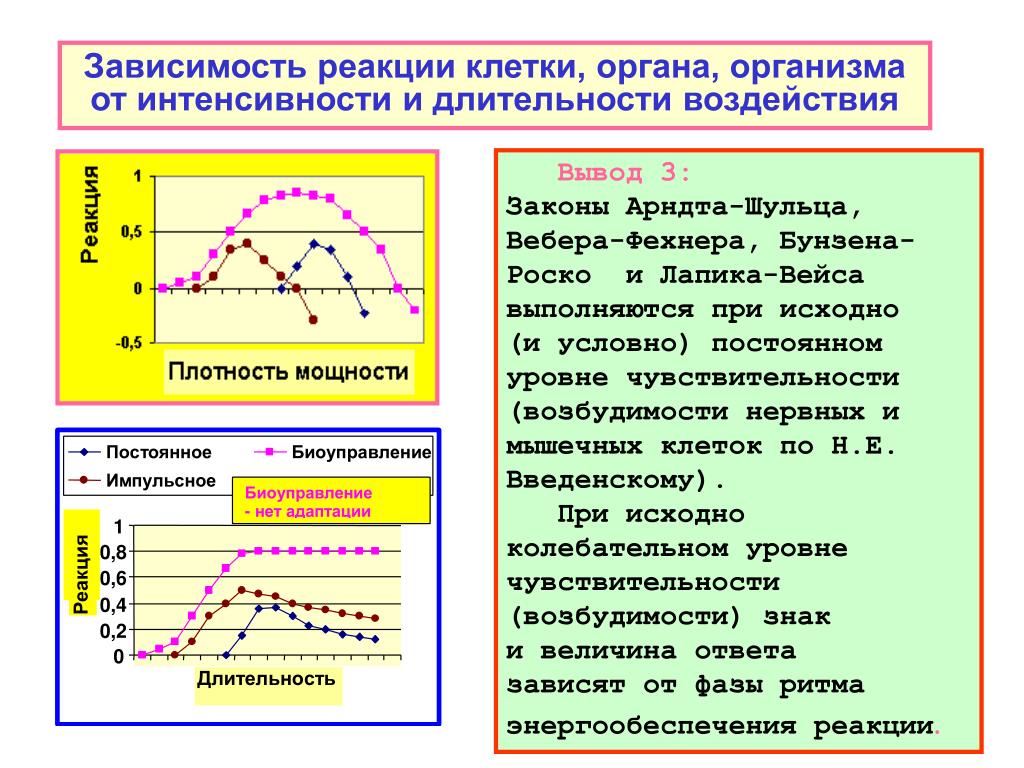
1.9. Психология БЖД |
Ан |
|
Закон Вебера-Фехнера на примере лампочек и бумажек :: SYL.ru
«Интенсивность ощущения пропорциональна логарифму интенсивности стимула» — так звучит формулировка закона Вебера-Фехнера. Сразу видно, умные слова, глубокий смысл в них и ценная информация… Понимать бы еще, что все это значит! А как раз в этом мы сейчас и разберемся… Итак, начнем по порядку. Во-первых, нужно разобраться с тем, чей это закон и при каких обстоятельствах он появился в уме своего создателя.
Кто такой «Вебер-Фехнер»?
Для начала, немного изучим того человека, который является непосредственно создателем закона Вебера-Фехнера. И сразу же поправочка… Их два. Нет, не закона, а человека.
Эрнст Генрих Вебер — это психофизиолог и анатом из Германии и брат известного физика Вильгельма Эдуарда Вебера, в честь которого даже была названа единица измерения магнитного потока.
Густав Теодор Фехнер — психолог из Германии, а также основоположник психофизиологии и психофизики.
История экспериментов и сущность закона Вебера-Фехнера
История зарождения этого закона началась еще в далеком одна тысяча восемьсот тридцать четвертом году, когда начали проводиться первые эксперименты Эрнста Вебера. Как раз в них ученый показал, что ощущения от нового раздражителя будут отличительны от раздражений, получаемых новым раздражителем в том случае, если интенсивность нового будет отличаться от интенсивности старого на величину, которая будет пропорциональна интенсивности предыдущего раздражителя. А уже, основываясь на этих экспериментах, Густав Фехнер сформулировал закон, о котором говорилось в данной статье выше. Закон Вебера-Фехнера в психологии также оставил большой след.
Формула закона
Ранее рассмотренная формулировка закона Вебера-Фехнера приобрела даже свою особую формулу: p=k*log{S}\{S_0} — сила ощущения пропорциональна логарифму интенсивности раздражителя.
В этой формуле S_0 — будет являться значением, которое отражает интенсивность раздражителя.
Расшифровка формулировки закона
Для того чтобы понять эти слова лучше, представьте перед собой люстру, которая имеет восемь лампочек и все они включены. Также представьте люстры с четырьмя включенными лампочками и третью люстру со всего лишь двумя включенными лампочками. Согласитесь, первая люстра настолько же ярче второй, насколько вторая ярче третьей… Для того чтобы у нас возникало ощущение постоянного прироста яркости, количества лампочек в люстре должно будет увеличиваться в разы. И в тот же момент, наоборот! Нам может казаться, что прирост яркости уменьшается в тот момент, когда увеличивается количество включенных лампочек в люстре. Чтобы понять это, представьте, словно перед вами находится люстра с двенадцатью включенными лампочками. А после этого представьте люстру, в которой будут включены тринадцать лампочек. Вы ведь тоже практически не замечаете, что яркость увеличилась? Но если бы мы добавили одну лампочку к той люстре, что состояла из двух, то не было бы места вопросу об увеличении яркости света, исходящего от люстры.
Итак, были подтверждены наблюдения, что человек способен чувствовать совсем не любые раздражения, а только те, которые обладают достаточно большой интенсивностью.
Пороги чувствительности в законе Вебера-Фехнера
Было обнаружено, что для того, чтобы человека почувствовал на себе действие того или иного раздражителя, его интенсивность должна будет достичь определенного уровня. Нижний порог чувствительности — это слабое и едва заметно воздействие интенсивности.
Логичным и правильным будет предположение о том, что помимо нижнего порога чувствительности существует также и верхний порог. Это тот уровень воздействия, после увеличения которого чувства уже не способны делаться сильнее.
Любое из воздействий на себя человек может чувствовать исключительно в промежутке между двумя этими состояниями. Именно из-за этого их называют внешними порогами чувствительности (или внешними порогами ощущения).
Стоит упомянуть и о том, что невозможно существовать параллелизму между интенсивностями чувствительности и раздражения, даже в межпороговом промежутке.
Расшифровка порогов чувствительности
Приведем тому пример… А для этого представьте, словно в руки вы берете какую-либо сумку, которая обладает некоторым весом. Теперь положите в вашу сумку бумажный лист. На самом деле, теперь вес сумки увеличился. Но вы этого не чувствуете, хотя эта разница находится в промежутки между этими двумя порогами чувствительности.
В данном случае можно рассуждать о том, что увеличение раздражения, на самом деле, слишком мало. Порогом различения называется та величина, на которую увеличивается раздражение. Теперь можно сделать вывод о том, что раздражение со слишком малым порогом различения является допороговым, а со слишком сильным, наоборот, запороговым. Но так же уровень таких показателей зависит от чувствительности различения. Чем выше чувствительность к ней, тем ниже порог различения.
Именно Вебер был первым человеком, который обратил внимание на то, что порог различения может быть абсолютным и релятивным. Очень важно отличать первый от второго. Абсолютным порогом является тот прирост интенсивности раздражения, который необходим, чтобы достичь порога различения. Снова приведем пример.
Абсолютным порогом является тот прирост интенсивности раздражения, который необходим, чтобы достичь порога различения. Снова приведем пример.
Чтобы почувствовать изменение двух тысячи граммового веса, к нему следует добавить еще двести грамм веса. Эта величина и является абсолютным порогом чувствительности. Но в случае, если вес нашего раздражителя составляет четыре тысячи грамм, этих двух сот грамм нам окажется недостаточно для того, чтобы ощутить на себе разницу.
Если эти же двести грамм представить числом, выражающим отношение между добавочным раздражением и основным раздражением, то это окажется релятивным порогом различения.
Такова вся сущность закона Вебера-Фехнера.
Теория оцифровки закона Вебера – Фехнера
3.1 Специальный вывод
В уравнении
для всех практических целей S ≥ S 0 . В уравнении
для всех практических целей P ≤ P 0 . Мы можем интерпретировать P 0 = 1 как порог P . Что наиболее важно, мы можем интерпретировать I как ответ на P ; Было бы неплохо для нас назвать P причудливым стимулом.Однако этот странный стимул принципиально отличается от других обычных физических стимулов тем, что это просто число, не имеющее физической единицы. Еще один очень важный факт: чем выше P , тем ниже I , а чем выше S , тем выше R . Но не обязательно, что I является строго убывающей функцией по отношению к P , а R является строго возрастающей функцией по отношению к S .Существенно важными фактами является то, что R и I по отношению к S и P , соответственно, являются логарифмическими и что оба S и P имеют пороговые значения. Следовательно, с этих точек зрения автор не может выбрать, но сказать, что вероятность возникновения является аномальным видом стимула. Было бы уместно назвать вероятность появления «математическим стимулом», поскольку вероятность появления не имеет физической единицы.
Что наиболее важно, мы можем интерпретировать I как ответ на P ; Было бы неплохо для нас назвать P причудливым стимулом.Однако этот странный стимул принципиально отличается от других обычных физических стимулов тем, что это просто число, не имеющее физической единицы. Еще один очень важный факт: чем выше P , тем ниже I , а чем выше S , тем выше R . Но не обязательно, что I является строго убывающей функцией по отношению к P , а R является строго возрастающей функцией по отношению к S .Существенно важными фактами является то, что R и I по отношению к S и P , соответственно, являются логарифмическими и что оба S и P имеют пороговые значения. Следовательно, с этих точек зрения автор не может выбрать, но сказать, что вероятность возникновения является аномальным видом стимула. Было бы уместно назвать вероятность появления «математическим стимулом», поскольку вероятность появления не имеет физической единицы.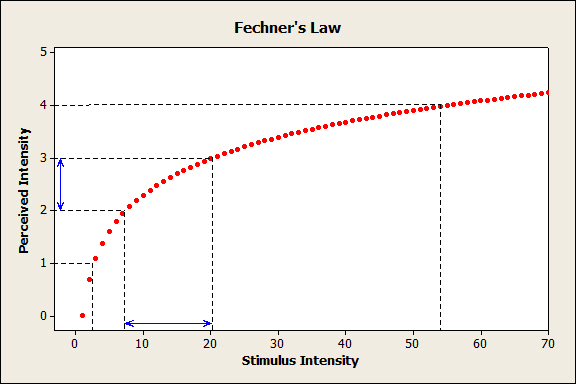 Этот математический стимул подчиняется закону Вебера – Фехнера. Расширяя диапазон приложений закона Вебера – Фехнера, мы получаем возможность комбинировать теорию информации с законом Вебера – Фехнера психофизики.
Этот математический стимул подчиняется закону Вебера – Фехнера. Расширяя диапазон приложений закона Вебера – Фехнера, мы получаем возможность комбинировать теорию информации с законом Вебера – Фехнера психофизики.
Для простоты в текущем подразделе мы установили K на 1 для всех ощущений. (Мы даем полное описание в подразделе 3.2. В этом подразделе мы не делаем никаких предположений относительно K .) Тогда мы можем сказать, что величина восприятия равна 0 бит, когда S = S 0 и что количество восприятия составляет 1 бит, когда S = 2 S 0 .Но есть одна вещь, о которой нужно быть осторожным. Реально у разных людей разные S 0 s. Таким образом, у разных людей разный объем информации об ответах на один и тот же S . Кроме того, по мере старения тела человека изменяется S 0 . Так, для идентичного S информационное наполнение ответа даже человека меняется с возрастом. Из-за этого информационное наполнение ответа сильно отличается от информационного содержания Шеннона.В определяющем уравнении информационного содержания Шеннона P 0 зафиксировано на 1.
Из-за этого информационное наполнение ответа сильно отличается от информационного содержания Шеннона.В определяющем уравнении информационного содержания Шеннона P 0 зафиксировано на 1.
Если физическим стимулом является вес, проблема проста. Чтобы четко определить новый вид энтропии, давайте теперь рассмотрим звуковую волну. Поскольку чистый тон, представляющий собой звуковую волну с синусоидальной формой волны, характеризуется как частотой, так и амплитудой смещения, рассмотрение только частоты или амплитуды может быть бессмысленным. Таким образом, мы рассматриваем и то, и другое одновременно.Для аргументации рассмотрим чистый тон с частотой f и амплитудой A . Физическая энтропия и энтропия Шеннона подчиняются ограничению, согласно которому общая сумма вероятностей равна 1. С другой стороны, в определяющем уравнении энтропии нового типа нет такого ограничения. Физические величины A и f изменяются гораздо более свободно. Следовательно, невозможно определить новую энтропию в той же форме, что и энтропия Шеннона.Другими словами, мы не должны определять новую энтропию как
который имеет форму энтропии Шеннона. Прежде чем мы определим новую энтропию, мы сначала определим общий объем ответа как
где измеряется в битах. Другими словами, общий объем ответа определяется так, чтобы он равнялся сумме сумм каждого отдельного ответа. Следовательно, мы определяем новую энтропию как среднее арифметическое рассматриваемого информационного содержания ответа; то есть новая энтропия определяется как
Следовательно, невозможно определить новую энтропию в той же форме, что и энтропия Шеннона.Другими словами, мы не должны определять новую энтропию как
который имеет форму энтропии Шеннона. Прежде чем мы определим новую энтропию, мы сначала определим общий объем ответа как
где измеряется в битах. Другими словами, общий объем ответа определяется так, чтобы он равнялся сумме сумм каждого отдельного ответа. Следовательно, мы определяем новую энтропию как среднее арифметическое рассматриваемого информационного содержания ответа; то есть новая энтропия определяется как
Единица измерения — бит / ответ.Обратите внимание, что в текущей ситуации есть два ответа: один из-за амплитуды, а другой из-за частоты. Автор называет эту новую величину «энтропией восприятия» или «процентом». Термин «процентная доля» — это новое сложное слово, образованное из восприятия и энтропии. Процентропия не полностью соответствует энтропии Шеннона. Тем не менее, полезно определить понятие процентропии. Одна из причин заключается в том, что процентропия напрямую связана с физической энергией.Мы легко можем понять такой факт. В качестве примера рассмотрим два чистых тона. Один тон имеет амплитуду A 1 и частоту f 1 . Другой тон имеет амплитуду A 2 и частоту f 2 . Процентропия прежнего тона составляет. Процентропия последнего тона составляет. A 1 f 1 = A 2 f 2 является необходимым и достаточным условием того, что процентные соотношения двух тонов одинаковы.И, A 1 f 1 = A 2 f 2 тогда и только тогда, когда ( A 1 f 1 ) 2 = ( A 2 f 2 ) 2 . Таким образом, мы можем сразу сделать вывод, что A 1 f 1 = A 2 f 2 является необходимым и достаточным условием того, что энергии двух тонов являются одно и тоже.
Одна из причин заключается в том, что процентропия напрямую связана с физической энергией.Мы легко можем понять такой факт. В качестве примера рассмотрим два чистых тона. Один тон имеет амплитуду A 1 и частоту f 1 . Другой тон имеет амплитуду A 2 и частоту f 2 . Процентропия прежнего тона составляет. Процентропия последнего тона составляет. A 1 f 1 = A 2 f 2 является необходимым и достаточным условием того, что процентные соотношения двух тонов одинаковы.И, A 1 f 1 = A 2 f 2 тогда и только тогда, когда ( A 1 f 1 ) 2 = ( A 2 f 2 ) 2 . Таким образом, мы можем сразу сделать вывод, что A 1 f 1 = A 2 f 2 является необходимым и достаточным условием того, что энергии двух тонов являются одно и тоже. Давайте теперь рассмотрим два составных тона. Один составной тон состоит из чистого тона с амплитудой A 11 и частотой f 11 и чистого тона с амплитудой A 12 и частотой f 12 . Другой составной тон состоит из чистого тона с амплитудой A 21 и частотой f 21 и чистого тона с амплитудой A 22 и частотой f 22 .Процентропия первого сложного тона составляет
Давайте теперь рассмотрим два составных тона. Один составной тон состоит из чистого тона с амплитудой A 11 и частотой f 11 и чистого тона с амплитудой A 12 и частотой f 12 . Другой составной тон состоит из чистого тона с амплитудой A 21 и частотой f 21 и чистого тона с амплитудой A 22 и частотой f 22 .Процентропия первого сложного тона составляет
Процентропия последнего составного тона равна
A 11 f 11 A 12 f 12 = A 21 f 21 A 06 22 22 является необходимым и достаточным условием того, что процентные содержания двух составных тонов одинаковы. А, A 11 f 11 A 12 f 12 = A 21 f 21 A f тогда и только тогда, когда ( A 11 f 11 ) 2 ( A 12 f 12 ) 2 = ( A 21 f 21 f 21 ) 2 ( A 22 f 22 ) 2 . Следовательно, в этой ситуации составных тонов равенство двух процентных соотношений является необходимым и достаточным условием того, что произведения энергий двух чистых тонов, составляющих каждый составной тон, одинаковы.
Следовательно, в этой ситуации составных тонов равенство двух процентных соотношений является необходимым и достаточным условием того, что произведения энергий двух чистых тонов, составляющих каждый составной тон, одинаковы.
3.3 Использование и интерпретация
Согласно нашей теории, становится возможным, что мы используем процентропию (или общий объем информации о реакции) для количественной оценки чувствительности органов чувств человека; в это время чувствительность зависит от стимулов и их пороговых значений.Эта количественная оценка позволяет нам сравнивать чувствительность органов чувств людей. Удивительно, но чувствительность сенсорного органа подразумевает превосходство сенсорного органа. Лучше всего объяснить на примере. Для простоты положим K = 1 для всех ощущений. Рассмотрим случай судебного заседания. Есть два человека. Для человека X A 0 = 33 вечера и f 0 = 20 Гц. Для другого человека Y, A 0 = 22 часа и f 0 = 60 Гц. Предположим, что два человека слышат звуковую волну с амплитудой 330 пм и частотой 1000 Гц. Тогда процентропия органа слуха X равна
а Y —
Предположим, что два человека слышат звуковую волну с амплитудой 330 пм и частотой 1000 Гц. Тогда процентропия органа слуха X равна
а Y —
Таким образом, орган слуха X превосходит орган Y. На самом деле, как мы можем очень легко понять, нам нужно знать только A 0 f 0 каждого человека для сравнения превосходства слуха. органы людей. Следовательно, можно сказать, что информационно-теоретическая мера превосходства органов слуха людей равна A 0 f 0 .Конечно, мы могли бы легко разработать A 0 f 0 в качестве меры превосходства без каких-либо знаний, описанных в этой статье. Ключевым моментом здесь является то, что мера A 0 f 0 оправдана теорией оцифровки закона Вебера – Фехнера; то есть A 0 f 0 является действительным с теоретико-информационной точки зрения. Обратите внимание, что мы установили K = 1 независимо от типа ощущения.
Обратите внимание, что мы установили K = 1 независимо от типа ощущения.
Даже если не предположить, что K = 1 для всех ощущений, мы все равно можем сравнивать чувствительность органов чувств людей. Но мера превосходства уже не A 0 f 0 . Если мы предположим, что все значения K A s для людей идентичны и что значения K f s для людей идентичны, тогда мера превосходства будет равна.
Так это хорошо. Тогда возникает вопрос, что означают 4,483 бит / ответ и 3,983 бит / ответ; эквивалентно, что означают 8,966 бит и 7,966 бит. Предположим, что действуют постоянные физические раздражители. Понятно: информационное содержание ответа пропорционально продолжительности ответа; что нет существенной разницы между продолжительностью ответа и продолжительностью внешнего стимула. И, наверное, квантуется длительность ответа. Другими словами, продолжительность ответа всегда является целым числом, кратным элементарной продолжительности. Согласно этой гипотезе, информационное содержание ответа в течение некоторого интервала времени равно некоторому целому числу, умноженному на содержание информации ответа в течение элементарной продолжительности. Следовательно, всякий раз, когда мы говорим о числовом значении K , мы должны вместе упоминать продолжительность ответа. Но сделать это громоздко. Следовательно, удобно сначала определить числовое значение K для элементарной продолжительности, а затем использовать определенное таким образом значение. Теперь мы можем сказать, что такое 8.Значит 966 бит и 7,966 бит. 7,966 битов — это определенное количество раз больше информационного содержания ответа для элементарной продолжительности.
Согласно этой гипотезе, информационное содержание ответа в течение некоторого интервала времени равно некоторому целому числу, умноженному на содержание информации ответа в течение элементарной продолжительности. Следовательно, всякий раз, когда мы говорим о числовом значении K , мы должны вместе упоминать продолжительность ответа. Но сделать это громоздко. Следовательно, удобно сначала определить числовое значение K для элементарной продолжительности, а затем использовать определенное таким образом значение. Теперь мы можем сказать, что такое 8.Значит 966 бит и 7,966 бит. 7,966 битов — это определенное количество раз больше информационного содержания ответа для элементарной продолжительности.
Закон Вебера
Закон ВебераВебера Закон
E. Х. Вебер в 1834 г. высказал следующее мнение:
Номер в этот пример выдуман; на практике ваши ценности могут отличаться.
Если поднять
и удерживая вес 2,0 кг, вы заметите
что это требует некоторых усилий. Если добавить к этому весу еще 0,05
кг и подъем, вы можете не заметить никакой разницы между видимым и
субъективный вес между 2,0 кг и 2,1
кг веса. Если вы продолжите прибавлять в весе, вы можете обнаружить, что
обратите внимание на разницу, когда дополнительный вес равен 0,2
кг. Порог приращения для определения разницы от 2,0 кг
вес 0,2 кг. Заметная разница (jnd) составляет 0,2
кг.
Если добавить к этому весу еще 0,05
кг и подъем, вы можете не заметить никакой разницы между видимым и
субъективный вес между 2,0 кг и 2,1
кг веса. Если вы продолжите прибавлять в весе, вы можете обнаружить, что
обратите внимание на разницу, когда дополнительный вес равен 0,2
кг. Порог приращения для определения разницы от 2,0 кг
вес 0,2 кг. Заметная разница (jnd) составляет 0,2
кг.
Теперь начнем с 5.Вес 0 кг. Если добавить к этому вес, вы обнаружите, что просто заметная разница составляет 0,5 кг. Нужно добавить 0,5 кг к 5,0 кг веса, чтобы вы заметили очевидную разницу.
Для веса величиной, I, 2,0 кг, порог прибавки для обнаружения разницы был я (произносит, дельта I) 0,2 кг.
Для веса величины, I = 5,0 кг, порог приращения I = 0,5 кг.
Соотношение
I / I для обоих
экземпляры (0.2 / 2,0 = 0,5 / 5,0 = 0,1) то же самое. Это Вебера
Закон .
Вебера Закон гласит, что отношение порога приращения к интенсивности фона является постоянным. Поэтому, когда вы находитесь в шумной обстановке, вы должны кричать, чтобы вас услышали, а шепот работает в тихом помещении. И когда вы измеряете пороги приращения на различных интенсивности фона пороги увеличиваются пропорционально фону.
Дробь Я / я известен как фракция Вебера (также известная как фракция Фехнера).Если преобразовать уравнение в I = IK, ты можно видеть, что закон Вебера предсказывает линейную зависимость между приращением порог и интенсивность фона. Ниже представлен график некоторых гипотетических данные, показывающие закон Вебера. Наклон линии — это фракция Вебера.
А TVI участок
Порог
В зависимости от интенсивности
иногда называют графиком TVR для пороговых значений
для обнаружения света (пороговое значение в зависимости от яркости).
Закон Вебера не всегда верно, но это хорошая отправная точка для сравнения производительности и как правило большого пальца.
На участке журнала (I) vs log I, наклон полученной прямой равен единице, если выполняется закон Вебера.
А модифицированный версия закона Вебера выглядит следующим образом:
где а — константа, обычно небольшая, которая представляет базовый уровень активности, нужно превзойти.
вот реально данные Агилара и Стайлза (1954), отображающие пороговые значения прироста.
Каждая кривая отображает одни и те же данные по-разному, используя две оси y. Посмотри, сможешь ли ты интерпретировать данные? Где приблизительно верен закон Вебера?
|
Продолжить
по закону |
границ | Единая теория психофизических законов восприятия силы звука
Введение
Психофизические законы пытаются связать амплитуду физического стимула с его воспринимаемой величиной, например громкость как функцию звукового давления или яркость как функцию яркости. Классический подход к раскрытию психофизических законов был предложен Фехнером (1966) в середине 18 века (оригинальная работа опубликована в 1860 году). Фехнер предположил, что едва заметная разница (jnd), выраженная как доля Вебера (Δ I / I ), где I — стандартная интенсивность звука, а Δ I — изменение интенсивности, необходимое для jnd, производит такое же приращение ощущения громкости (Δ L ). Интегрируя это уравнение, а именно Δ L = Δ I / I , он получил так называемый закон Фехнера: громкость является логарифмической функцией интенсивности звука ( L = lg I ).
Классический подход к раскрытию психофизических законов был предложен Фехнером (1966) в середине 18 века (оригинальная работа опубликована в 1860 году). Фехнер предположил, что едва заметная разница (jnd), выраженная как доля Вебера (Δ I / I ), где I — стандартная интенсивность звука, а Δ I — изменение интенсивности, необходимое для jnd, производит такое же приращение ощущения громкости (Δ L ). Интегрируя это уравнение, а именно Δ L = Δ I / I , он получил так называемый закон Фехнера: громкость является логарифмической функцией интенсивности звука ( L = lg I ).
Не только логарифмический закон Фехнера был заменен степенным законом Стивенса или L = I θ , где θ — константа (Stevens, 1961), но и его общий подход был поставлен под сомнение из-за невозможности интегрировать jnd-функции два разных звука, чтобы предсказать их соответствующие функции громкости (Newman, 1933; Miller, 1947). Таким образом, неудивительно, что некоторые исследователи отказались от фехнеровского подхода к установлению связи между стимулом jnd и субъективной величиной.Что удивительно, так это основания отказа от фехнеровского подхода. Например, Стивенс (1961) утверждал, что метод прямой оценки величины устарел различение интенсивности как меру отношения между стимулом и ощущением. Он рассматривал меру дискриминации как «инженер говорит… разброс некоторых настроек шкалы». В совершенно противоположной точке зрения Вимейстер и Бэкон (1988) заявили, что данные оценки громкости были мерой с «вероятно сильным участием несенсорных факторов, (и) мы не пытались связать эти данные с данными для различения интенсивности.”
Таким образом, неудивительно, что некоторые исследователи отказались от фехнеровского подхода к установлению связи между стимулом jnd и субъективной величиной.Что удивительно, так это основания отказа от фехнеровского подхода. Например, Стивенс (1961) утверждал, что метод прямой оценки величины устарел различение интенсивности как меру отношения между стимулом и ощущением. Он рассматривал меру дискриминации как «инженер говорит… разброс некоторых настроек шкалы». В совершенно противоположной точке зрения Вимейстер и Бэкон (1988) заявили, что данные оценки громкости были мерой с «вероятно сильным участием несенсорных факторов, (и) мы не пытались связать эти данные с данными для различения интенсивности.”
Были и другие исследователи, которые продолжали продвигать фехнеровский подход в поисках единой теории, связывающей различение интенсивности с функцией громкости. Первоначальное предположение Фехнера иногда называли теорией «наклона», потому что оно предсказывало, что чем круче функция громкости, тем меньше jnd или доля Вебера для постоянного увеличения громкости. Этот простой прогноз наклона оказался неверным, по крайней мере, в случаях набора громкости, когда потеря слуха улитки или частичная маскировка повышали порог слышимости, но вызывали аномально резкий рост громкости, так что нормальная громкость воспринималась при высоких уровнях звука (Fowler, 1937). .Чтобы объяснить несостоятельность теории наклона Фехнера, несколько исследователей предложили теорию «пропорционального jnd», в которой размер jnd необходимо нормировать на общее число jnd в динамическом диапазоне стимула (Riesz, 1933; Teghtsoonian, 1971; Lim и др., 1977). С другой стороны, теория «равной громкости, равной-jnd» утверждала, что jnd не имеет никакого отношения к наклону функции громкости, а скорее определяется общей громкостью (Zwislocki and Jordan, 1986). Несмотря на значительные усилия по тестированию этих соотношений громкость-jnd, консенсуса пока не достигнуто (Houtsma et al., 1980; Hellman et al., 1987; Schlauch and Wier, 1987; Ранкович и др., 1988; Джонсон и др., 1993; Стиллман и др.
Этот простой прогноз наклона оказался неверным, по крайней мере, в случаях набора громкости, когда потеря слуха улитки или частичная маскировка повышали порог слышимости, но вызывали аномально резкий рост громкости, так что нормальная громкость воспринималась при высоких уровнях звука (Fowler, 1937). .Чтобы объяснить несостоятельность теории наклона Фехнера, несколько исследователей предложили теорию «пропорционального jnd», в которой размер jnd необходимо нормировать на общее число jnd в динамическом диапазоне стимула (Riesz, 1933; Teghtsoonian, 1971; Lim и др., 1977). С другой стороны, теория «равной громкости, равной-jnd» утверждала, что jnd не имеет никакого отношения к наклону функции громкости, а скорее определяется общей громкостью (Zwislocki and Jordan, 1986). Несмотря на значительные усилия по тестированию этих соотношений громкость-jnd, консенсуса пока не достигнуто (Houtsma et al., 1980; Hellman et al., 1987; Schlauch and Wier, 1987; Ранкович и др., 1988; Джонсон и др., 1993; Стиллман и др. , 1993; Schlauch et al., 1995; Аллен и Нили, 1997; Хеллман и Хеллман, 2001).
, 1993; Schlauch et al., 1995; Аллен и Нили, 1997; Хеллман и Хеллман, 2001).
Здесь я представляю единую теорию, начиная с общей формы функции громкости Zwislocki (1965), чтобы вывести общую форму закона Брентано, и я приду к общей форме отношения громкость-jnd, которая объединяет предыдущие теории громкости-jnd. . В частности, я считаю, что предыдущие теории «наклона», «пропорционального jnd» и «равной громкости, равного jnd» являются тремя дополнительными терминами в новой единой теории.Я также показываю, что новая теория способна предсказывать громкость и данные jnd в широком диапазоне слуховых ситуаций, включая нейросенсорную тугоухость, одновременную маскировку, прямую маскировку и электрический слух.
Вывод единой теории
Получение общей формы закона Брентано или Экмана
Я начинаю с общей формы функции громкости, предложенной Zwislocki (1965; уравнение 212):
L = k [(I + cI0) θ- (cI0) θ] (1)
, где I 0 — порог обнаружения для определенного типа звука, c представляет масштабный коэффициент внутреннего шума, а k — постоянная величина.
Общность и симметрия — две причины для выбора функции громкости Цвислока. Во-первых, при высоких интенсивностях ( I ≫ I o ) функцию Цвислока можно упростить до степенного закона Стивенса, а именно: L = kI θ . При низкой интенсивности Цвислоки сделал неявное, но важное предположение для учета набора громкости вблизи порога: наклон (θ) функции громкости не увеличивается, как первоначально предполагалось (Fowler, 1937), вместо этого увеличивается громкость на пороге.Установка I = I o в уравнении. (1), громкость на пороге, или L o = k [( I o + cI o ) θ — ( cI o ) θ ] = k [( 1 / c + 1 ) θ — 1)] ( cI o ) θ 901 k60 ∼ [θ ( 1 / c ) 1 – θ ] ( I o ) θ , прямо пропорционально пороговому значению и «должно быть больше нуля (Zwislocki, 1965; стр. .87) ». Математически громкость на пороге бесконечна, когда внутренний шум равен нулю ( c = 0), и наоборот. Это фундаментальный аргумент в пользу того, почему мозг имеет или нуждается во внутреннем шуме, потому что бесконечная громкость явно биологически неприемлема. Концепция внутреннего шума Цвислоки также была расширена, чтобы сформировать основу для рассмотрения набора громкости как «невосприятия мягкости» (Buus and Florentine, 2002), а тиннитуса как «дополнительного центрального шума» (Zeng, 2013). В интересах простоты я определяю громкость на пороге как: L o = k ( cI o ) θ (или c = 0.125 для θ = 0,27).
.87) ». Математически громкость на пороге бесконечна, когда внутренний шум равен нулю ( c = 0), и наоборот. Это фундаментальный аргумент в пользу того, почему мозг имеет или нуждается во внутреннем шуме, потому что бесконечная громкость явно биологически неприемлема. Концепция внутреннего шума Цвислоки также была расширена, чтобы сформировать основу для рассмотрения набора громкости как «невосприятия мягкости» (Buus and Florentine, 2002), а тиннитуса как «дополнительного центрального шума» (Zeng, 2013). В интересах простоты я определяю громкость на пороге как: L o = k ( cI o ) θ (или c = 0.125 для θ = 0,27).
Во-вторых, математическую симметрию можно показать, дифференцируя уравнение. (1):
ΔLΔI = θk (I + cI0) θ-1 = θk (I + cI0) θI + cI0 (2)
Складывая и вычитая тот же компонент в приведенном выше уравнении, я получаю:
ΔLΔI = θk (I + cI0) θ- (cI0) θ + (cI0) θI + cI0 = θL + L0I + cI0 (3)
Переписывая приведенное выше уравнение, я получаю общую форму закона Брентано или закона Экмана, а именно ΔLL = ΔII (обсуждение этих законов см. В Stevens, 1961):
В Stevens, 1961):
ΔLL + L0 = θΔII + cI0 (4)
Уравнение (4) математически симметрично и сбалансировано, имеет общую форму закона Вебера, включающую пороговый поправочный член как в области ощущений ( L o ), так и в области стимулов (c I ). o ).
В первом приближении закон Вебера в области стимулов был «воспроизведен в сотнях исследований с использованием всех сенсорных модальностей и многих видов животных за последние два столетия (Pardo-Vazquez et al., 2019)». При распознавании интенсивности звука доля Вебера постоянна для широкополосного шума, но немного уменьшается с увеличением интенсивности, что приводит к «близкому нарушению» закона Вебера (McGill and Goldberg, 1968). Следовательно, уравнение. (4) можно записать как:
ΔLL + L0 = wIα (5)
, где w и α — константы, причем α = 0 указывает на полное соответствие закону Вебера.
Согласно теории «пропорционального jnd» (Лим и др. , 1977), константа w обратно пропорциональна количеству jnds ( N ) в динамическом диапазоне стимула. Другими словами, w = 1/ N , что можно рассматривать как коэффициент масштабирования, чтобы учесть тот факт, что разные субъекты или разные типы стимулов могут иметь разное количество различимых шагов в их соответствующем динамическом диапазоне (например, , у слушателя с нормальным слухом есть 100 шагов, а у пользователя кохлеарного имплантата — только 10), но все они имеют одинаковый рост громкости от тихого на пороговом уровне до неприятно громкого на верхнем пределе диапазона.Теория «пропорционального jnd» утверждает, что 10 шагов jnd у слушателя с нормальным слухом вызовут такое же изменение громкости, как и шаг jnd у пользователя кохлеарного имплантата. Хотя теория «пропорционального jnd» не предполагала и не требовала какой-либо конкретной функции jnd-громкости, Лим и др. (1977) намекнули, что закон Брентано «почти правильный» (см. Сноску 7 на стр. 1264 в Lim et al.
, 1977), константа w обратно пропорциональна количеству jnds ( N ) в динамическом диапазоне стимула. Другими словами, w = 1/ N , что можно рассматривать как коэффициент масштабирования, чтобы учесть тот факт, что разные субъекты или разные типы стимулов могут иметь разное количество различимых шагов в их соответствующем динамическом диапазоне (например, , у слушателя с нормальным слухом есть 100 шагов, а у пользователя кохлеарного имплантата — только 10), но все они имеют одинаковый рост громкости от тихого на пороговом уровне до неприятно громкого на верхнем пределе диапазона.Теория «пропорционального jnd» утверждает, что 10 шагов jnd у слушателя с нормальным слухом вызовут такое же изменение громкости, как и шаг jnd у пользователя кохлеарного имплантата. Хотя теория «пропорционального jnd» не предполагала и не требовала какой-либо конкретной функции jnd-громкости, Лим и др. (1977) намекнули, что закон Брентано «почти правильный» (см. Сноску 7 на стр. 1264 в Lim et al. , 1977). В этом случае относительное изменение громкости обратно пропорционально количеству jnds с поправкой на интенсивность, происхождение которой будет рассмотрено в разделе «Обсуждение»:
, 1977). В этом случае относительное изменение громкости обратно пропорционально количеству jnds с поправкой на интенсивность, происхождение которой будет рассмотрено в разделе «Обсуждение»:
ΔLL + L0 = 1NIα (6)
Прогнозирование функции jnd на основе функции баланса громкости
Предположим, что функция громкости для тихого тона равна: L = f (I) , и что получена функция баланса громкости между тихим тоном и тоном в маскировке: I = г (Я м ). По определению, при I = г (I m ) громкость сбалансирована, так что функция громкости может быть получена для частично замаскированного тона:
Lm = L = f (I) = f [g (Im)] (7)
Дифференцируя приведенное выше уравнение, получаем:
ΔLmΔIm = f ′ (I) g ′ (Im) = ΔLΔIg ′ (Im) (8)
Перепишите приведенное выше уравнение:
ΔIm = ΔI1g ′ (Im) ΔLmΔL (9)
Заменить Δ L м и Δ L формулой. (6) чтобы получить:
(6) чтобы получить:
ΔIm = ΔI1g ′ (Im) NNmImαIαLm + LmoL + Lo (10)
Чтобы предсказать jnd в виде фракции Вебера при той же интенсивности, то есть I m = I , чтобы можно было исключить поправочный член интенсивности (Imα / Iα) и разделить вышеприведенное уравнение по ( I ):
ΔImI = ΔII1g ′ (Im) NNmLm + LmoL + Lo (11)
Используя логарифмическое преобразование, можно вычислить jnd через долю Вебера в дБ (WFdB):
WFmdB (I) = WFdB (I) -10logg ′ (Im) + 10logNNm + 10logLm + LmoL + Lo (12)
, где WF м дБ (I) = 10log (Δ I m / I ), что является логарифмической долей Вебера для замаскированного тона и WFdB (I) = 10log ( Δ I / I ), которая является долей Вебера для тона в тишине.
Уравнение (12) указывает, что, если WFdB (I) известен при данной интенсивности ( I ), то можно предсказать WF м дБ (I) с той же интенсивностью из трех дополнительных измеряет: (1) локальный наклон функции баланса громкости [ g ‘ ( I m )], (2) коэффициент масштабирования ( N / N m ) и (3) локальное соотношение громкости между замаскированным тоном и тоном в тишине [( L м + L мес ) / (L + L o )].Интересно, что теоретически нет необходимости точно знать порог обнаружения, точную форму увеличения громкости или функцию распознавания интенсивности для тона в тишине.
Я рассматриваю уравнение. (12) в качестве единой теории психофизических законов восприятия интенсивности звука, потому что последние три члена в уравнении содержат три предыдущие теории, которые пытались связать функцию jnd с функцией громкости. Член 10log г ’ ( I м ) представляет собой первоначальную теорию« наклона »Фехнера; термин 10log ( N / N m ) представляет собой «пропорциональную» теорию Рисса; а последний термин представляет теорию Цвислоцкого «равной громкости, равной громкости».
Подтверждение единой теории
Прогнозирование jnd-функций при одновременном маскировании
Одновременное маскирование не только повышает порог чистого тона, но также влияет на восприятие его громкости, подобно набору громкости при нейросенсорной тугоухости. Функции баланса громкости и распознавания интенсивности были измерены в одной и той же группе слушателей для чистых тонов в тишине и при одновременном маскировании шума (Houtsma et al., 1980; Rankovic et al., 1988; Schlauch et al., 1995).
Здесь я использую Schlauch et al. (1995) данные для прогнозирования замаскированного jnd из тихого jnd, поскольку Schlauch et al. (1995) имел наиболее полный набор данных. Рисунок 1 иллюстрирует относительные вклады трех специальных членов в уравнении. (12) к предсказаниям jnd-данных при одновременном маскировании. На рисунке 1A показаны три функции баланса громкости: сплошная линия представляет гипотетическое состояние, при котором один и тот же тон идеально сбалансирован по громкости (т.е., соотношение 1: 1) между двумя ушами в тишине, пунктирная линия представляет измеренную функцию баланса для замаскированного тона в широкополосном шуме 15-SPL / Гц, а пунктирная линия для замаскированного тона в SPL / 40-дБ / Широкополосный шум Гц (из рисунка 3 в Schlauch et al., 1995). Затем дифференцируется интерполяция функции баланса громкости для получения наклонов в зависимости от интенсивности (X представляют маскирование 15 дБ SPL / Гц, а O представляют условие маскирования 40 дБ SPL / Гц). На рисунке 1B показана функция увеличения громкости для тона 1000 Гц в тишине (сплошная линия), основанная на модели Цвислока [уравнение.(1), используя k = 3,1; θ = 0,27; c = 2,5; I o = 10 — 12 Вт / м 2 или 0 дБ SPL], а также две функции замаскированного увеличения громкости, полученные путем применения функций баланса громкости на рисунке 1A к функция увеличения громкости в тишине. Значки X и O представляют собой соотношение громкости между соответствующими условиями тишины и маскировки. На рисунке 1C показаны измеренные функции jnd в режиме тихого (сплошная линия), маскирования на 15 дБ (пунктирная линия) и при маскировании на 40 дБ (пунктирная линия).Значки X и O представляют собой предсказанные значения jnd в двух вышеупомянутых условиях маскирования на основе уравнения. (12). В дополнение к использованию значений наклона на рисунке 1A и значений отношения громкости на рисунке 1B, уравнение. (12) использует коэффициент нормализации 4 дБ и 8 дБ для условий маскирования 15 дБ и 40 дБ соответственно. Коэффициенты нормализации 4 дБ и 8 дБ были оценены как по динамическому диапазону, так и по значениям jnd (Nelson et al., 1996; см. Их рисунок 9), при этом тихое состояние было в 2,5 раза больше и 6.В 3 раза больше шагов jnd, чем при условии маскирования 15 дБ и 40 дБ соответственно. В этом прогнозе не было свободного параметра. Что касается относительного вклада в успешное предсказание, теория «равной громкости, равной-jnd» была существенной для предсказания общей тенденции (та же нисходящая картина на рисунках 1B, C), в то время как теория наклона (относительно пологая Образец символов X и O на рисунке 1A) ведет себя аналогично теории пропорционального jnd в качестве константы для сдвига предсказанной функции вверх или вниз.
Рис. 1. Прогнозы при одновременном маскировании с данными (линиями), полученными Schlauch et al. (1995). Панель (A) показывает функции баланса громкости между тоном в тишине ( y -ось) и тоном в шуме ( x -ось). два уха в тишине, пунктирная линия представляет функцию баланса для тона, маскируемого широкополосным шумом 15 дБ SPL / Гц, а пунктирная линия представляет функцию баланса громкости для тона шумом 40 дБ SPL / Гц.Символы представляют значения наклона для функции баланса. Значения наклона используют тот же масштаб, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны. Панель (B) показывает производные функции роста громкости. Символы представляют значения отношения громкости между тихими и замаскированными тонами и тонами в тихом режиме. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).
Прогнозирование функции jnd при прямом маскировании
На громкость и ее jnd-функции стимула также может влиять прямая и обратная маскировка.Увеличивается громкость и снижается различение интенсивности при прямом и обратном маскировании, особенно при средней интенсивности (Zeng et al., 1991; Plack and Viemeister, 1992; Zeng and Turner, 1992). Хотя ранняя попытка связать «горб среднего уровня» (функция jnd) с повышением громкости не увенчалась успехом (Zeng, 1994), Оберфельд (2008) обнаружил значительную корреляцию между повышенным jnd и повышенной громкостью при широком диапазоне маскирующих звуков. тестировались разности уровней сигнала.
Используя те же шаги обработки, что и на рисунках 1, 2, показана функция баланса громкости между тоном длительностью 25 мс в тишине и при наличии 90 дБ УЗД, 100 мс прямого маскера (рисунок 2A), полученное увеличение громкости функция (рисунок 2B), а также измеренные и прогнозируемые функции jnd в тихом и маскированном режимах (рисунок 2C).Теория наклона (рисунок 2A) предсказывала, что прямое маскирование будет давать меньшие, чем нормальные jnds для стандартных уровней ниже 50 дБ SPL, но большие jnds для уровней выше 50 дБ SPL. Теория «равной громкости, равного jnd» (рис. 2B) предсказала среднеуровневую функцию горба jnd из-за повышенной громкости при прямом маскировании. Коэффициент нормализации 7 дБ, или в пять раз меньше jnd шагов при прямом маскировании, был использован в окончательном успешном прогнозе (рис. 2C), который объединил все три специальные теории в формуле. (12).Подобная картина на рисунках 2B, C в целом согласуется с наблюдаемой корреляцией между повышенной громкостью и повышенным jnd (Oberfeld, 2008), но количественный прогноз требует дальнейшего изучения. Было бы также интересно узнать, может ли существующая объединенная теория предсказать аналогичную функцию jnd, наблюдаемую для коротких высокочастотных тонов в условиях режекторного шума (Carlyon and Moore, 1984). Оксенхэм и Мур (1995) намекнули на такую возможность, предложив «новую теорию, [объясняющую] резкое отклонение от закона Вебера с точки зрения как дисперсии…, так и громкости частично замаскированных сигналов.”
Рис. 2. Прогнозы при прямом маскировании с данными (линиями) из Zeng (1994). Панель (A) показывает функции баланса громкости между тоном в тишине ( y -ось) и тоном с прямой маскировкой ( x -ось): сплошная линия представляет состояние управления, при котором один и тот же тон был сбалансирован между два уха в тишине, а пунктирная линия представляет функцию баланса для тона при прямой маскировке. Символы * представляют значения наклона для функции баланса, которая использует ту же шкалу, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны.Панель (B) показывает производные функции роста громкости. Символы представляют значения отношения громкости между замаскированным тоном и тоном в тишине. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).
Прогнозирование jnd-функций в электрическом слухе
В электрическом слухе, где волосковые клетки отсутствуют, а волокна слухового нерва напрямую стимулируются электрическим током, громкость обычно имеет узкий динамический диапазон 10–20 дБ (Zeng and Galvin, 1999).Зенг и Шеннон (1994) обнаружили, что у пользователей кохлеарных имплантатов громкость растет как традиционная степенная функция электрического тока для частот стимула ниже 300 Гц, но как экспоненциальная функция для частот стимула выше 300 Гц. Эти две разные функции увеличения громкости будут производить функцию логарифмического баланса громкости между низко- и высокочастотными электрическими стимулами. На рисунке 3A действительно показана такая функция логарифмического баланса (сплошные линии) между стимулом 100 Гц (синусоида или амплитуда импульса на оси y ) и синусоидой 1000 Гц (ось x ).
Рис. 3. Баланс громкости (A) и функции JND (B) у пользователей кохлеарных имплантатов. (A) Функции баланса громкости были получены между синусоидальным импульсом 100 Гц или импульсом 100 Гц и синусоидальным электрическим стимулом 1000 Гц, адаптированным из рисунков 2D, E в Zeng and Shannon (1994). Печатается с разрешения AAAS. Символы представляют индивидуальные данные, а сплошная линия представляет функцию логарифмического баланса. Пунктирная линия представляет функцию линейного баланса, которая явно не соответствовала действительности. (B) Данные JND (символы) и предсказанные функции (линии) с использованием одних и тех же стимулов от одних и тех же субъектов в (A) , адаптированном из рисунка 4 в Zeng and Shannon (1999). Печатается с разрешения Wolters Kluwer Health.
E1000 Гц = θlogE100 Гц (13)
, где θ — наклон функции логарифмического баланса громкости. Дифференцируя приведенное выше уравнение, чтобы получить следующую функцию JND между высокочастотными и низкочастотными электрическими стимулами:
ΔE1000 Гц = θΔE100 ГцE100 Гц (14)
Зенг и Шеннон (1999) измерили jnds этих стимулов у тех же пациентов с имплантатом (символы на рисунке 3B) и обнаружили, что не только эта функция jnd сохраняется, но, что более важно, функция jnd была почти постоянной (сплошная линия на рисунке 3B). .Учитывая такую же функцию увеличения громкости мощности для электрических стимулов с частотой 100 Гц, неудивительно, что их доля Вебера также была постоянной. Но почему абсолютная разница (Δ E 1000 Гц ) была постоянной для стимула с частотой 1000 Гц? Зенг и Шеннон (1999) показали, что эта постоянная абсолютная разница является результатом функции экспоненциального роста громкости.
L1000Hz = exp (E1000Hz) (15)
Дифференцируя приведенное выше уравнение, получаем:
ΔL1000HzΔE1000Hz = exp (E1000Hz) = L1000Hz (16)
Переписывая приведенное выше уравнение, получаем:
ΔL1000ГцL1000Гц = ΔE1000Гц (17)
Уравнение (17) означает, что коэффициент Брентано также постоянен при электростимуляции.Единственная разница между уравнениями. (17) и (4) состоит в том, что (17) не содержит порогового члена, вероятно, из-за отсутствия спонтанной нервной активности в глухом ухе (Kiang and Moxon, 1972).
Обсуждение
Ни один из отдельных компонентов существующей единой теории не является новым. Предыдущие исследования предлагали эти отдельные теории и оценивали их по отдельности (например, Zwislocki and Jordan, 1986; Hellman and Hellman, 1990, 2001; Schlauch, 1994; Schlauch et al., 1995; Allen and Neely, 1997).Настоящее исследование является новым в двух отношениях. Во-первых, настоящее исследование объединяет ранее отключенные отдельные компоненты с помощью единой теоретической основы, а именно общей формы закона Брентано в формуле. (4). Во-вторых, настоящее исследование предлагает новую формулу, а именно уравнение. (12), который специально сочетает эти отдельные термины для успешного прогнозирования соотношений громкости и jnd при одновременной и прямой маскировке, а также у пользователей кохлеарных имплантатов. Настоящая единая теория и ее успешные применения предполагают, что, хотя закон Вебера необходимо заменить общей формой закона Брентано, первоначальная идея Фехнера об использовании jnds для вывода психофизических законов действительна, по крайней мере, в широком диапазоне рассматриваемых здесь слуховых ситуаций.
Общая форма закона Брентано может быть использована для проверки того, насколько близко фактические данные jnd соответствуют закону Вебера и его потенциальным механизмам, путем комбинирования уравнений. (4) и (5):
ΔLL + L0 = θΔII + cI0 = wIα или ΔII + cI0 = w′Iα (18)
, где как w ’ (= w / θ), так и α являются свободными параметрами, подлежащими оценке, причем α = 0 указывает на полное соответствие закону Вебера. На рисунке 4 показаны данные jnd и оценка модели для тона 1 кГц (Schlauch et al., 1995), широкополосного шума 8 кГц (6–14 кГц) и того же шума на фоне шума с зазубринами (Viemeister, 1983). .Все три набора данных могут быть смоделированы двухэтапной функцией с крутым первым этапом (∼10–20 дБ SPL), отражающим пороговое влияние, и более мелким вторым этапом (∼20–100 дБ SPL) с крутизной α в формуле. (16). Все три набора данных подчиняются закону Вебера (McGill and Goldberg, 1968), где α составляет -0,09 для тона, -0,03 для шума и 0,04 для шума на фоне шума с зазубринами. Ближайший промах находится в диапазоне от -9% до 4% и составляет в среднем 3% для трех рассматриваемых здесь стимулов.
Рисунок 4. Прогнозирование JND для шумовых и тональных стимулов. Данные JND для широкополосного шума (сплошные треугольники) и того же шума на фоне шума с надрезом (сплошные квадраты) были взяты из Viemeister (1983; те же символы на его рисунке 1) и данных JND тона 1000 Гц (открытые кружки) ) взяты из Schlauch et al. (1995; кружки на рис. 2 в правом нижнем углу). Пунктирная линия представляет собой прогноз функции JND шума, пунктирная линия представляет шум на фоне шума с выемками, а сплошная линия представляет функцию JND тона.
Чтобы найти решение почти пропуска закона Вебера, Макгилл и Голдберг использовали процесс, подобный Пуассону, в котором среднее значение громкости ( L ) и его дисперсия (σ 2 ) равны, где σ — величина стандартное отклонение. Для достижения 75% правильного обнаружения в jnd задаче теория обнаружения сигналов требует: d ′ = ΔLσ = ΔLL0,5 = 1 (Green and Swets, 1966). Замена Δ L = L 0,5 в уравнении. (19) произвести:
ΔLL + L0 = L0.5L + L0∝L-0.5∝ (I0,27) -0,5∝I-0,14 (19)
По сравнению с крутизной -0,14, предсказанной пуассоновским процессом, расчетная крутизна составляла 5% для тона, 11% для шума и 18% для шума на фоне режекторного шума. В качестве чрезмерной коррекции решение Макгилла и Голдберга создало гораздо большую разницу (в среднем = 11%), чем исходная проблема, то есть почти полное отсутствие (в среднем = 3%) закона Вебера. С другой стороны, использование распространения сигнала возбуждения является более вероятным механизмом, лежащим в основе почти несоблюдения закона Вебера (Florentine and Buus, 1981; Viemeister, 1983), но количественная обработка его предсказательной точности все еще отсутствует.По крайней мере, в первом приближении закон Вебера справедлив для различения интенсивности звука.
Несмотря на то, что это непросто, поиск единого психофизического закона продолжает привлекать внимание, особенно его биологическая основа (например, Shepard, 1987; Nieder and Miller, 2003; Dehaene et al., 2008; Джафаров и Колониус, 2011; Техцунян, 2012; Pardo-Vazquez et al., 2019). Во влиятельной статье, которая привлекла 30 открытых комментариев коллег, Крюгер (1989) попытался примирить Фехнера и Стивенса, предложив единый психофизический закон, в котором (1) «каждый jnd имеет одинаковую субъективную величину для данной модальности» (2). ) «Субъективная величина увеличивается примерно как степенная функция физической величины» и (3) «субъективная величина зависит в первую очередь от периферических сенсорных процессов, то есть не происходит никаких нелинейных центральных преобразований.Что касается (1), Крюгер предпочел Δ S или в настоящем термине Δ L = c (константа) для закона экономии, но был готов принять Δ L / L = c (закон Брентано) или даже Δ L / L = L −0,5 (процесс Пуассона Макгилла и Голдберга). Настоящее исследование отдает предпочтение закону Брентано с пороговым поправочным коэффициентом. Второй момент был главной задачей единого закона Крюгера, в котором он не только пытался согласовать различные способы измерения величины ощущений (например,g., оценка величины по сравнению с категориальным рейтингом), но также вывести функцию субъективной величины из данных jnd. Он подробно исследовал «теорию пропорционального jnd» (стр. 260), неявно обсуждал теорию «наклона» (его таблица 1 на стр. 261), но, вероятно, не знал о «равной громкости, равном jnd» теории, не говоря уже о том, чтобы рассматривать их как три независимых фактора, которые вместе вносят вклад в функцию jnd-громкости (настоящее исследование). Третий пункт Крюгера, относящийся к мозгу как к линейному устройству, неверен, потому что настоящее исследование (B3) не только показывает, что электрическая стимуляция слухового нерва, которая обходит слуховые волосковые клетки, вызывает экспоненциальную функцию громкости у пользователей кохлеарных имплантатов, но и что еще более важно, многие исследования нейропластичности обнаружили аномально повышенный прирост в головном мозге в ответ на снижение входного сигнала на периферии (например,г., Qiu et al., 2000; Норена, 2011; Chambers et al., 2016).
Заявление о доступности данныхНаборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.
Заявление об этике
Этическое одобрение для этого исследования не требовалось, поскольку данные на людях были взяты из ранее опубликованных исследований. Пациенты / участники предоставили письменное информированное согласие на участие в этом исследовании.
Авторские взносы
F-GZ несет полную ответственность за представленные здесь работы.
Конфликт интересов
Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Джо Цвислоки стимулировал мой интерес к этому предмету, когда я был аспирантом, посещающим его классы в Сиракузском университете. Я многому научился, а также получил пользу от интеллектуальных дискуссий с Крисом Тернером, Нилом Вимейстером, Бертом Шлаухом, Адрианом Хаутсмой, Бобом Шенноном, Уолтом Джестедтом, Джонтом Алленом, Брайаном Муром, Бобом Карлайоном, Крисом Плэком, Дунканом Люсом, Биллом МакГиллом, Бертом. Шарф, Рона и Билл Хеллман.Маике ван Экхаутте мотивировала обсуждение закона Вебера (рис. 4), Даниэль Оберфельд и Вольфганг Эллермайер сделали критические комментарии, которые помогли связать несколько неясных концов и расширить рамки обсуждения в этой статье. Однако я несу полную ответственность за представленные здесь работы.
Список литературы
Аллен, Дж. Б., и Нили, С. Т. (1997). Моделирование отношения между едва заметной разницей в интенсивности и громкостью для чистых тонов и широкополосного шума. Дж.Акуст. Soc. Являюсь. 102, 3628–3646. DOI: 10.1121 / 1.420150
CrossRef Полный текст | Google Scholar
Buus, S., и Florentine, M. (2002). Рост громкости у слушателей с улитковой тугоухостью: пересмотр набора. J. Assoc. Res. Отоларингол. 3, 120–139. DOI: 10.1007 / s101620010084
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Карлайон Р. П. и Мур Б. С. (1984). Дискриминация по интенсивности: серьезный отход от закона Вебера. J. Acoust. Soc. Являюсь. 76, 1369–1376. DOI: 10.1121 / 1.3
CrossRef Полный текст | Google Scholar
Чемберс, А. Р., Резник, Дж., Юань, Ю., Уиттон, Дж. П., Эдж, А. С., Либерман, М. С. и др. (2016). Центральное усиление восстанавливает слуховую обработку после почти полной денервации улитки. Neuron 89, 867–879. DOI: 10.1016 / j.neuron.2015.12.041
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Дехаэн, С., Изард, В., Спелке, Э., и Пика, П. (2008). Логарифмический или линейный? Четкое интуитивное понимание числовой шкалы в культурах коренных народов Запада и Амазонки. Наука 320, 1217–1220. DOI: 10.1126 / science.1156540
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фехнер, Г. Т. (1966). Elemente der Psychophysik [Элементы психофизики]. Нью-Йорк, Нью-Йорк: Холт, Райнхарт и Уинстон, Инк.
Google Scholar
Florentine, M., and Buus, S. (1981). Модель возбуждающего паттерна для распознавания интенсивности. J. Acoust. Soc. Являюсь. 70, 1646–1654. DOI: 10.1121 / 1.387219
CrossRef Полный текст | Google Scholar
Фаулер, Э. П. (1937). Измерение ощущения громкости — новый подход к физиологии слуха, функциональным и дифференциально-диагностическим тестам. Arch. Отоларингол. 26, 514–521. DOI: 10.1001 / archotol.1937.00650020568002
CrossRef Полный текст | Google Scholar
Грин Д. М. и Светс Дж. А. (1966). Теория обнаружения сигналов и психофизика. Нью-Йорк, Нью-Йорк: Wiley.
Google Scholar
Хеллман Р., Шарф Б., Техцунян М. и Техцунян Р. (1987). О связи между ростом громкости и различением интенсивности чистых тонов. J. Acoust. Soc. Являюсь. 82, 448–453. DOI: 10.1121 / 1.395445
CrossRef Полный текст | Google Scholar
Хеллман, В. С., и Хеллман, Р. П. (1990). Дискриминация по интенсивности как движущая сила громкости. Применение к чистым тонам в тишине. J. Acoust. Soc. Являюсь. 87, 1255–1265. DOI: 10.1121 / 1.398801
CrossRef Полный текст | Google Scholar
Хеллман, У. С., и Хеллман, Р. П. (2001). Пересмотр отношений между громкостью и различением интенсивности. J. Acoust. Soc. Являюсь. 109 (5 Pt 1), 2098–2102. DOI: 10.1121 / 1.1366373
CrossRef Полный текст | Google Scholar
Хаутсма, А. Дж., Дурлах, Н. И., и Брейда, Л. Д. (1980). Восприятие интенсивности XI. Экспериментальные результаты по отношению разрешения по интенсивности к согласованию громкости. J. Acoust. Soc. Являюсь. 68, 807–813. DOI: 10.1121 / 1.384819
CrossRef Полный текст | Google Scholar
Джонсон, Дж. Х., Тернер, К. У., Цвислоки, Дж. Дж. И Марголис, Р. Х. (1993). Просто заметные различия в интенсивности и их отношении к громкости. J. Acoust. Soc. Являюсь. 93, 983–991. DOI: 10.1121 / 1.405404
CrossRef Полный текст | Google Scholar
Кианг, Н. Ю. и Моксон, Э. К. (1972). Психологические соображения при искусственной стимуляции внутреннего уха. Ann. Отол. Ринол. Ларингол. 81, 714–730. DOI: 10.1177 / 000348947208100513
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Крюгер, Л. Э. (1989). Примирение Фехнера и Стивенса — к единому психофизическому закону. Behav. Brain Sci. 12, 251–267. DOI: 10.1017 / S0140525x0004855x
CrossRef Полный текст | Google Scholar
Лим, Дж. С., Рабиновиц, В. М., Брейда, Л. Д., и Дурлах, Н. И. (1977). Восприятие интенсивности.VIII. Сравнение громкости между разными типами стимулов. J. Acoust. Soc. Являюсь. 62, 1256–1267. DOI: 10.1121 / 1.381641
CrossRef Полный текст | Google Scholar
МакГилл, У. Дж., И Голдберг, Дж. (1968). Исследование близких к неудачам с участием закона Вебера и дискриминации по интенсивности тона. Восприятие. Психофизика. 4, 105–109. DOI: 10.3758 / bf03209518
CrossRef Полный текст | Google Scholar
Миллер, Г. (1947). Чувствительность к изменениям интенсивности белого шума и его отношение к маскировке и громкости. J. Acoust. Soc. Являюсь. 19, 609–619. DOI: 10.1121 / 1.1
- 8
- Представьте, что вы добровольно участвуете в психологическом эксперименте в своей школе.Исследователи просят вас держать по два небольших количества песка в каждой руке. Экспериментатор медленно добавляет крошечные количества песка в одну руку и просит вас сказать, когда вы замечаете, что одна рука кажется тяжелее другой. Наименьшая разница в весе, которую вы можете обнаружить хотя бы в половине случаев, — это просто заметная разница.
- Вы смотрите телевизор со своим супругом, но громкость слишком низкая, чтобы слышать. Вы просите своего супруга включить его. Он дважды нажимает кнопку громкости, но разницы в громкости все равно не заметить.Ваш супруг нажимает кнопку еще два раза, прежде чем вы заметите увеличение громкости.
- Вы устраиваете вечеринку в вашей квартире, и к вам подходит сосед и просит выключить музыку. Вы и ваши гости сразу замечаете, что музыка намного тише, но ваш сосед не замечает разницы в громкости, потому что изменение ниже его порога разницы.
- Вы добровольно участвуете в другом психологическом эксперименте в своей школе. На этот раз экспериментаторы кладут небольшое количество сахара в емкость с водой и просят вас выпить.Вас просят сказать, когда вы замечаете сладость воды по сравнению с простой водой. Наименьший уровень сладости, который вы можете попробовать в половине случаев, — это порог разницы.
CrossRef Полный текст | Google Scholar
Нельсон Д. А., Шмитц Дж. Л., Дональдсон Г. С., Вимейстер Н. Ф. и Джавел Э. (1996). Распознавание интенсивности в зависимости от уровня раздражителя при электрическом раздражении. J. Acoust. Soc. Являюсь. 100 (4 Pt 1), 2393–2414. DOI: 10.1121 / 1.417949
CrossRef Полный текст | Google Scholar
Ньюман, Э. (1933). В справедливости просто заметна разница как единица психологической величины. Пер. Kansas Acad. Sci. 36, 172–175. DOI: 10.2307 / 3625353
CrossRef Полный текст | Google Scholar
Нидер, А., Миллер, Э. К. (2003). Кодирование когнитивной величины: сжатое масштабирование числовой информации в префронтальной коре приматов. Нейрон 37, 149–157. DOI: 10.1016 / s0896-6273 (02) 01144-1143
CrossRef Полный текст | Google Scholar
Норена А. Дж. (2011). Интегративная модель тиннитуса, основанная на центральном усилении, контролирующем нервную чувствительность. Neurosci. Biobehav. Ред. 35, 1089–1109. DOI: 10.1016 / j.neubiorev.2010.11.003
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Оберфельд Д. (2008). Горбинка средней разницы при замаскированной в прямом направлении дискриминации по интенсивности. J. Acoust. Soc. Являюсь. 123, 1571–1581. DOI: 10.1121 / 1.2837284
CrossRef Полный текст | Google Scholar
Oxenham, A.J., и Moore, B.C.J. (1995). Превышение и серьезное отклонение от закона о веберах. Дж.Акуст. Soc. Являюсь. 97, 2442–2453. DOI: 10.1121 / 1.411965
CrossRef Полный текст | Google Scholar
Pardo-Vazquez, J. L., Castineiras-de Saa, J. R., Valente, M., Damiao, I., Costa, T., Vicente, M. I., et al. (2019). Механистическая основа закона Вебера. Нац. Neurosci. 22, 1493–1502. DOI: 10.1038 / s41593-019-0439-7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Плак, К. Дж., И Вимейстер, Н. Ф. (1992). Дискриминация по интенсивности при обратной маскировке. J. Acoust. Soc. Являюсь. 92, 3097–3101. DOI: 10.1121 / 1.404205
CrossRef Полный текст | Google Scholar
Цю К., Салви Р., Динг Д. и Буркард Р. (2000). Потеря внутренних волосковых клеток приводит к увеличению амплитуды ответа в слуховой коре неанестезированных шиншилл: свидетельство увеличения системного усиления. Слушайте. Res. 139, 153–171. DOI: 10.1016 / s0378-5955 (99) 00171-9
CrossRef Полный текст | Google Scholar
Ранкович, К. М., Вимейстер, Н.Ф., Фантини Д. А., Чизман М. Ф. и Учияма К. Л. (1988). Соотношение между громкостью и разницей интенсивности составляет величину для тонов на тихом и шумном фоне. J. Acoust. Soc. Являюсь. 84, 150–155. DOI: 10.1121 / 1.396981
CrossRef Полный текст | Google Scholar
Riesz, R. (1933). Отношение между громкостью и минимальным заметным приращением интенсивности. J. Acoust. Soc. Являюсь. 4, 211–216. DOI: 10.1121 / 1.11
CrossRef Полный текст | Google Scholar
Schlauch, R.С. (1994). Разрешение по интенсивности и громкость в высокочастотном шуме. J. Acoust. Soc. Являюсь. 95, 2171–2179. DOI: 10.1121 / 1.410017
CrossRef Полный текст | Google Scholar
Шлаух Р. С., Харви С. и Лантье Н. (1995). Разрешение по интенсивности и громкость в широкополосном шуме. J. Acoust. Soc. Являюсь. 98, 1895–1902. DOI: 10.1121 / 1.413375
CrossRef Полный текст | Google Scholar
Стивенс, С. С. (1961). Чтобы почтить память Фехнера и отменить его закон: степенная функция, а не логарифмическая функция, описывает рабочие характеристики сенсорной системы. Наука 133, 80–86. DOI: 10.1126 / science.133.3446.80
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Стиллман, Дж. А., Цвислоки, Дж. Дж., Чжан, М., и Чефаратти, Л. К. (1993). Просто заметные различия в интенсивности при одинаковой громкости в нормальном и патологическом ушах. J. Acoust. Soc. Являюсь. 93, 425–434. DOI: 10.1121 / 1.405622
CrossRef Полный текст | Google Scholar
Техцунян Р. (2012). Стандартная модель воспринимаемой величины: основа для (почти) всего, что о ней известно. Am. J. Psychol. 125, 165–174. DOI: 10.5406 / amerjpsyc.125.2.0165
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вимейстер, Н. Ф., и Бэкон, С. П. (1988). Распознавание интенсивности, обнаружение приращения и оценка амплитуды для тонов с частотой 1 кГц. J. Acoust. Soc. Являюсь. 84, 172–178. DOI: 10.1121 / 1.396961
CrossRef Полный текст | Google Scholar
Цзэн Ф. Г. (1994). Рост громкости при прямой маскировке: отношение к различению интенсивности. J. Acoust. Soc. Являюсь. 96, 2127–2132. DOI: 10.1121 / 1.410154
CrossRef Полный текст | Google Scholar
Цзэн, Ф. Г. (2013). Модель активной громкости, предполагающая, что шум в ушах — это усиление центрального шума, а гиперакузия — как усиление нелинейного усиления. Слушайте. Res. 295, 172–179. DOI: 10.1016 / j.heares.2012.05.009
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Цзэн Ф. Г. и Шеннон Р. В. (1994). Механизмы кодирования громкости, полученные в результате электростимуляции слуховой системы человека. Наука 264, 564–566. DOI: 10.1126 / science.8160013
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Цзэн Ф. Г. и Тернер К. В. (1992). Дискриминация по интенсивности при прямой маскировке. J. Acoust. Soc. Являюсь. 92 (2 Pt 1), 782–787. DOI: 10.1121 / 1.403947
CrossRef Полный текст | Google Scholar
Цзэн Ф. Г., Тернер К. В. и Релкин Э. М. (1991). Восстановление после предшествующей стимуляции. II: влияние на различение интенсивности. Слушайте. Res. 55, 223–230. DOI: 10.1016 / 0378-5955 (91) -k
CrossRef Полный текст | Google Scholar
Zwislocki, J. (1965). «Анализ некоторых слуховых характеристик», в Справочнике по математической психологии , ред. Р. Люс, Р. Р. Буш и Э. Галантер (Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc.), 79–97.
Google Scholar
Zwislocki, J. J., and Jordan, H. N. (1986). Об отношении интенсивности jnd к громкости и нейронному шуму. J. Acoust. Soc. Являюсь. 79, 772–780. DOI: 10.1121 / 1.393467
CrossRef Полный текст | Google Scholar
(PDF) Закон Вебера-Фехнера и оптимальность логарифмической шкалы
Также в физике релевантной ошибкой является относительная ошибка. Точность физических мер
выражается в количестве значимых цифр на показателе
, что составляет количественную оценку относительной ошибки, причем каждая цифра обеспечивает 10-кратное уменьшение относительной ошибки
.Расстояния в астрономии часто измеряются в
световых года, а расстояние до ядер выражается в ангстремах. Этот факт также присутствует в повседневной жизни
, хотя и в не столь понятной форме. Продолжительность жизни взрослого человека составляет
лет, тогда как небольшие промежутки времени измеряются часами и минутами.
Для измерения продолжительности жизни человека в часах необходимо использовать 6-значное число, а не
, состоящее из 2-х цифр. Поэтому, используя годы вместо часов, мы экономим 4 цифры за счет ошибки
(в худшем случае) одного года.
Следует ожидать, что и в биологии относительная ошибка будет больше
, чем абсолютная ошибка.
Количество отдельных уровней, по которым классифицируется стимул (биологической системой
), должно быть ограничено из-за конечного характера обработки информации. Совершенно естественно предположить, что существует биологическая стоимость количества различных уровней
, которые организм использует для классификации и сравнения стимулов. Действительно, для этого числа должны быть анатомические /
функциональные ограничения.В классической работе Миллер (1956) показал
, что количество различных уровней, которые неподготовленный человек может использовать для классификации стимула
, составляет 7 ± 2. Объем обрабатываемой информации также влияет на скорость обработки информации в
, и, таким образом, это также ограничивает количество уровней
, на которых классифицируется стимул. Следовательно, следует ожидать, что эволюция
выбрала компактную систему классификации, но с наименьшей относительной ошибкой.Наша цель
— формально продемонстрировать, что максимальная относительная ошибка минимизирована логарифмической шкалой
, подтверждая логарифмическую шкалу как возможную цель для естественного отбора.
Модель квантования и относительной ошибки
Мы проанализируем проблему минимизации относительной ошибки количественной
классификации (квантования) стимула на фиксированное количество уровней или классов.
Это число N может меняться в зависимости от рассматриваемого стимула / восприятия —
и объекта.Грубо говоря, наша задача состоит в том, чтобы разделить интервал на фиксированное количество подинтервалов
и аппроксимировать все числа в каждом интервале единым фиксированным числом
, чтобы минимизировать относительную ошибку.
Мы предполагаем, что есть детектор, который измеряет интенсивность сигнала или
стимула. Для простоты мы предполагаем, что в измерении
нет ошибки, пока интенсивность находится в диапазоне [a, b], с 0 \ a \ b \ ?.
Минимальная интенсивность a является порогом детектора и для интенсивностей выше
b достигается насыщение. Теперь задача состоит в том, чтобы квантовать сигналы в диапазоне [a, b] в
шкале N уровней. Первый шаг — разделить интервал [a, b] на Nsub-
интервалов, используя N-1 промежуточных точек y1; … yN1, чтобы
a¼y0 \ y1 \ \ yN1 \ yN¼bð1Þ
и подынтервалы
I1¼½y0; y1Þ; I2½y1; y2Þ; …; IN¼½yN1; yN: ð2Þ
Закон Вебера-Фехнера и оптимальность логарифмической шкалы
123
Закон Вебера
Закон ВебераЗакон Вебера
Фон:
Закон Вебера часто записывают как:
ΔI / I = к
, где Δ означает «изменение», I означает интенсивность, а k — постоянная величина (помните, что Фехнер и Веберы были немцами, а по-немецки константа пишется константе.) ΔI должно быть читается как «изменение интенсивности, необходимое для того, чтобы просто заметить разницу», а иногда записывается как JND для «просто заметная разница». Собирая все вместе, закон Вебера гласит, что изменение интенсивности необходимо просто заметить изменение интенсивности, деленное на исходную интенсивность, всегда означает одно и то же значение k для a учитывая сенсорную модальность.
Небольшая алгебраическая обработка и замена эквивалентных членов в приведенной выше формуле дает:
JND = kI
Эта альтернатива говорит то же самое, но по-другому: изменение интенсивности, необходимое для просто обратите внимание, что разница (JND) пропорциональна (k) исходной интенсивности (I).Это означает, что низкая интенсивность раздражители (например, тусклый свет, тихий звук) требуют очень небольших изменений в их интенсивности, чтобы быть заметными. разные, но эти стимулы высокой интенсивности (например, яркий свет, громкий звук) требуют гораздо большего изменения их интенсивность должна быть просто заметно разной.
Вы могли бы испытать нечто подобное с 3-сторонней лампочкой. У трехходовой лампочки три настройки (помимо «выкл.») Например, он может иметь настройки 50 Вт, 100 Вт и 150 Вт. Если предположить, что Настройка 100 Вт дает вдвое больше света, чем настройка 50 Вт, поэтому вы легко можете увидеть закон Вебера в действии. Изменение мощности лампы с 50 до 100 Вт дает большую и легко заметную разницу в воспринимаемой яркости света. Однако изменение лампы со 100 до 150 Вт дает гораздо меньшую, не так легко заметную разницу в воспринимаемом яркость света.Это то, что предсказывает закон Вебера — для большей исходной интенсивности (100 Вт) требуется гораздо больше энергии. большее изменение интенсивности должно заметно отличаться от меньшей исходной интенсивности (50 Вт). такое же увеличение силы света лампы (от 50 до 100 Вт против 100 до 150 Вт) будет более заметно при нижнем интенсивнее, чем при более высокой интенсивности.
Вы можете использовать психофизическую процедуру, такую как метод настройки Фехнера, чтобы определить Фракция Вебера для данной сенсорной модальности.Например, вы можете измерить интенсивность звука. Например, интенсивность звука может быть 100 (я намеренно оставляю единицу измерения отключенной — на самом деле это не так неважно, что это за единица, если вы постоянно используете одну и ту же единицу на протяжении всего примера. Единицы отменит друг с другом, оставив дробь Вебера безразмерной величиной). увеличивайте интенсивность звука до тех пор, пока вы не заметите, что он стал громче, чем был изначально.В этом Например, чуть более громкий звук имеет интенсивность 104,8. Из этих двух чисел вы можете рассчитать Фракция Вебера:
ΔI / I = к
(104,8 — 100) / 100 = 0,048
ΔI — это изменение интенсивности, необходимое для того, чтобы просто заметить различия — это разница громких и мягких звуков: 104,8 — 100. Исходная интенсивность, I, равна 100. Выполнение математических расчетов дает дробь k, равная.048
Теперь, когда у нас есть фракция Вебера, мы можем использовать ее, чтобы судить, насколько звук должен быть громче любого другой звук, чтобы просто заметить, что он громче. Например, насколько громче должен быть звук, чтобы быть заметно громче звука с интенсивностью 50? Изменение в Интенсивность будет заметно отличаться:
JND = kI
JND = 0,048 x 50 = 2,4
Нам нужно добавить это значение к исходной интенсивности (I), чтобы получить интенсивность, которая была бы просто заметно отличается.50 + 2,4 = 52,4. Таким образом, человек должен уметь различать только громкость звука. звуки с интенсивностью 50 и 52. 4.
Мы могли бы легко выполнить последние два шага за один шаг:
Интенсивность, при которой разница становится заметной = I * (k + 1)
= 50 * (0,048 + 1)
= 52,4
Чтобы проверить свою работу, вы можете вычислить дробь Вебера, k, из этих двух значений.Должно по-прежнему равняется 0,048.
ΔI / I = к
(52,4 — 50) / 50 = 0,048
Проверьте свои знания
Для этих задач используйте определение закона Вебера, чтобы вычислить дробь Вебера, k, из два стимула, которые заметно различаются. Затем используйте дробь Вебера, чтобы решить, насколько разные стимулы должен быть от другого данного стимула, чтобы заметно отличаться.Введите свой ответ и нажмите «Проверить ответ». кнопка. Вы получите отзыв о правильности своего ответа, а также будет показано решение. Нажмите «Создайте новую проблему», чтобы создать другую проблему.
Закон Вебера в процессе принятия решений: интеграция поведенческих данных у людей с нейрофизиологической моделью
Историческая справка
Джонсон (1980a, b) тщательно проанализировал и сформулировал взаимосвязь между нейрофизиологическими измерениями (отражающими нейрональную репрезентацию сенсорной стимуляции на соматосенсорном пути) и поведением вероятностного субъекта, наблюдаемого психофизически.В частности, он предложил строгую теоретическую основу, включающую в качестве явных переменных экспериментальную установку, нейронные представления стимулов, дисперсию нейронных представлений и функциональную зависимость от стимулов, которые они представляют. В этой теоретической схеме он различал: (1) нейронные процессы, кодирующие информацию о периферических стимулах, на которой основано различение, и (2) нейронные процессы, лежащие в основе дискриминации при принятии решений в соответствии с экспериментальной установкой, которую он рассмотрел.Таким образом, Джонсон (1980a, b) смог связать закон Вебера с лежащими в основе нейронными механизмами.
Тем не менее, Джонсон (1980a, b) предположил линейные механизмы и предположил, что нейронное представление стимулов является результатом вызванной стимулом активности и шума. В этом исследовании мы дополняем и расширяем теорию Джонсона (1980a, b), предлагая конкретную реалистичную биофизическую нейронную сеть, реализующую принятие решений в задаче распознавания. Мы обращаемся к тому, как динамика нейронной сети может явно преобразовать базовую нейронную активность и шум в поведении конкретного субъекта.Более того, мы покажем, что динамическая рабочая точка нейронной сети является фундаментальной и неразрывно связана с вероятностным поведением субъектов.
Другими словами, мы предполагаем, как и Джонсон (1980a, b), что отличительной чертой нейрофизиологических измерений является высокая степень вариабельности нейрональной активности как в рамках испытаний, так и между ними. Вместо того, чтобы связывать эту изменчивость с плохой выборкой, мы предполагаем, что стохастические колебания в динамике нейронов могут действительно иметь функциональную роль.В самом деле, тот факт, что восприятие и поведение во время определенных типов задач могут быть хорошо описаны вероятностными моделями, предполагает связь между стохастичностью на клеточном и поведенческом уровнях. Основная цель настоящего исследования — выяснить механизмы, лежащие в основе этой связи, путем построения вычислительных моделей, которые учитывают измерения как на клеточном, так и на поведенческом уровнях.
Теоретическая основа: нейродинамическая модель
Теоретические модели могут помочь понять лежащие в основе нейродинамические и вычислительные механизмы, ответственные за оценку перцептивных свидетельств, ведущих к принятию решений (Brody et al., 2003; Machens et al., 2005; Deco and Rolls, 2006). Такие модели ограничиваются существующими нейрофизиологическими данными и согласуются с ними (Romo and Salinas, 2001, 2003; Romo et al., 2004). Обычно они включают две популяции возбуждающих нейронов, участвующих в конкурентных взаимодействиях, опосредованных ингибированием. Сенсорный ввод может смещать конкуренцию в пользу одной из популяций, потенциально приводя к постепенному принятию решения, при котором нейроны, принадлежащие к победившей популяции, проявляют повышенную активность, тогда как активность в другой популяции подавляется.
Мы смоделировали нейронную, синаптическую и корковую динамику, лежащую в основе вычисления перцепционной дискриминации, используя теоретическую основу сетей аттракторов (Brunel and Wang, 2001), основанную на принципе предвзятого соревнования / сотрудничества [см. Предыдущие приложения (Rolls and Deco, 2002). ; Deco and Rolls, 2005а, б)]. Эта модель была разработана для учета активности нейронов, реализующих процесс сравнения, обнаруженный в VPC, о чем свидетельствуют записи отдельных клеток и соответствующие показатели поведения у обезьян.Реакция этих нейронов в течение периода сравнения задачи зависит от разницы частот между двумя применяемыми вибротактильными стимулами, знак этой разницы является определяющим фактором для правильного выполнения задачи. Вычислительная модель Deco and Rolls (2006) реализует нейронную сеть, которая может воспроизводить избирательность реакции принятия решений упомянутых нейронов VPC. Механизмы конкуренции и сотрудничества реализуются в сети аттракторов, состоящей из двух периодически связанных популяций возбуждающих нейронов, взаимно связанных с общей тормозящей популяцией.
Модель позволяет надлежащим образом описывать переходные процессы (нестационарность) и вероятностную природу поведения (производительности) путем явного использования всплесков и синаптической динамики однокомпонентных моделей нейронов с интеграцией и запуском (IF) (Tuckwell, 1988) при микроскопический уровень. Это позволило нам использовать реалистичные биофизические постоянные времени, задержки и проводимости для моделирования синаптического тока, что позволило тщательно изучить временные масштабы и частоту возбуждения, участвующих в эволюции нейронной активности.Смоделированные здесь нейронные клетки IF имеют три типа рецепторов, опосредующих приток синаптических токов: EPSC опосредуются рецепторами AMPA (быстрые) и NMDA-глутамат (медленные), тогда как внешние EPSC, наложенные на сеть, управляются рецепторами AMPA. Только. IPSC к возбуждающим и тормозящим нейронам опосредуются рецепторами ГАМК [подробности математической формулировки см. В Brunel and Wang (2001) и Deco and Rolls (2005a, 2006)].
Аттракторная сеть, реализующая механизм сравнения (рис.1) состоит из взаимодействующих нейронов, организованных в дискретный набор популяций (то есть группы возбуждающих или тормозящих нейронов, имеющих одни и те же входы и связи). Сеть содержит 800 N E (возбуждающих) пирамидных клеток и 200 N I ингибирующих интернейронов в соответствии с пропорцией 80% пирамидных клеток по сравнению с 20% интернейронов, обычно наблюдаемых в физиологических исследованиях (Abeles, 1991; Роллс и Деко, 2002). В этой минимальной модели конкретные популяции кодируют категориальный результат сравнения двух последовательно применяемых вибротактильных стимулов, f1 и f2 (т.е.е., f1> f2 или f1
Биофизическая реалистичная вычислительная модель для вероятностной сети принятия решений, которая выполняет сравнение двух механических колебаний, применяемых последовательно (f1 и f2). Модель реализует динамическую конкуренцию между разными нейронами. Сеть содержит возбуждающие пирамидные клетки и тормозные интернейроны. Нейроны полностью связаны (с синаптической силой, как указано в тексте). Нейроны группируются в популяции. Есть два разных типа населения: возбуждающие и тормозящие.Существует два подтипа возбудительной популяции: специфическая и неселективная. Конкретные группы населения кодируют результат процесса сравнения в задаче вибротактильного различения с двумя интервалами (то есть, является ли f1> f2 или f1 Значения проводимости синапсов между парами нейронов определяются весами соединений, которые могут отклоняться от их значения по умолчанию, 1.Структура и функция сети достигается за счет различной адаптации этих синаптических сил внутри и между популяциями нейронов. Обозначение весов показано на рисунке 1. Мы предполагаем, что связи уже сформированы (например, с помощью ранее происходивших процессов самоорганизации, таких как обучение Хебба). Мы предполагаем, что два возможных результата решения, f1> f2 и f1 Стационарные состояния сети нейронов интегрирования и активации могут быть исчерпывающе изучены с использованием приведенного согласованного среднего поля, чтобы упростить уравнения интегрирования и включения путем замены, после диффузионного приближения (Tuckwell, 1988), суммы синаптические компоненты — средним компонентом и членом флуктуации. Стационарная динамика каждой популяции может быть описана функцией переноса населения, которая обеспечивает средний уровень популяции как функцию среднего входного тока.Набор стационарных самовоспроизводящихся скоростей ν i для различных популяций и в сети может быть найден путем решения набора связанных уравнений самосогласования. Это позволяет выбрать область параметров, которая показывает желаемое поведение на бифуркационной диаграмме. a В данном случае существенное требование состоит в том, чтобы для стационарных условий различные возможные аттракторы были устойчивыми. Аттракторы, представляющие интерес для нашей задачи, соответствуют активации (высокие скорости всплесков) или неактивации (низкие скорости всплесков) нейронов в определенных популяциях f1> f2 и f1 Мы протестировали группу из восьми человек (от 18 до 35 лет), которые вызвались участвовать в исследовании. Все были правши и сообщили о нормальной тактильной чувствительности. Участники сидели на расстоянии около 60 см от компьютерного монитора с электронно-лучевой трубкой в тускло освещенной, звуконепроницаемой испытательной комнате. Им было приказано направить взгляд на фиксирующий крест в центре экрана.Стимуляцию осуществляли с помощью вибротактильного стимулятора костной проводимости (вибраторы костной проводимости Oticon-A; вибрирующая поверхность 3,8 см 2 ; Oticon, Hamilton, UK). Протоколы были запрограммированы с использованием программного обеспечения Expe6 (Pallier et al., 1997) и запускались на компьютере ПК Pentium (Intel, Санта-Клара, Калифорния). Волны вибрации генерировались звуковой картой ПК и подавались на вибраторы через усилитель (Pioneer-A307; частотная характеристика от 5 Гц до 100 кГц). Стимулятор прикрепляли к дистальной подушечке левого кольцевого пальца с помощью тканевой петли на липучке, так что положение вибратора и давление оставались постоянными на протяжении всего сеанса эксперимента.Испытуемые носили наушники (HD435; Sennheisser, Wedemark, Germany), обеспечивающие белый шум постоянной интенсивности на протяжении всего эксперимента, достаточной для маскировки любого звука, производимого вибротактильными стимуляторами. Эксперимент по частотной дискриминации состоял из двух интервалов с принудительным выбором, в котором два 500 мс вибротактильных стимула (базовая и сравниваемая частоты, рандомизированный порядок, интервал между стимулами 500 мс) были представлены участнику для классификации.В начале каждого испытания на экране компьютера отображался знак «-» в центре, который временно заменялся знаком «*» во время представления каждой вибрации. После второй вибрации появится «?» знак появлялся в центре экрана, пока не был дан ответ. Задача заключалась в нажатии клавиши (1 или 2), соответствующей стимулу более высокой частоты (соответственно первому или второму). Были протестированы пять различных базовых частот (20, 30, 40, 60 и 80 Гц), хотя для тестирования модели использовались только частоты <50 Гц (флаттер).Это было сделано в попытке задействовать один и тот же тип соматосенсорных рецепторов и путей (рецепторы Мейснера) во всех условиях (Werner and Mountcastle, 1965; Mountcastle et al., 1967; Freeman and Johnson, 1982). Каждой конкретной базовой частоте противостояли восемь различных частот сравнения (± 2, ± 4, ± 6 и ± 8 Гц) в отдельном блоке из 112 испытаний (восемь комбинаций базовой частоты и частоты сравнения представлены по 14 раз каждая). На экспериментальной фазе участникам не было предоставлено никакой обратной связи.Перед этим тестом на распознавание вибрации интенсивность различных вибротактильных стимулов была тщательно отрегулирована индивидуально для каждого участника следующим образом. Учитывая, что воспринимаемая интенсивность вибрации варьируется в зависимости от частоты, потребовались определенные корректировки, чтобы участники основывали свои суждения на частоте. Во-первых, мы определили простой порог обнаружения для каждой базовой частоты, используя чередующиеся лестницы на основе оценки параметров с помощью алгоритма последовательного тестирования (PEST), чтобы отрегулировать усиление звуковой карты для обеспечения 50% эффективности обнаружения.После этой процедуры мы подняли уровень выходного сигнала усилителя на 15% и запустили вторую фазу, чтобы найти точку субъективного равенства интенсивности по вибротактильным частотам. В частности, мы постепенно настраивали выход звуковой карты [уровень звукового давления (SPL)] индивидуально для каждой частоты сравнения, чтобы она ощущалась такой же интенсивной, как и соответствующая базовая частота (мы использовали чередующиеся лестницы PEST). Затем для каждого участника и базовой частоты мы нашли наиболее подходящую линию (линейная регрессия) для описания взаимосвязи между частотой (для всех частот сравнения) и SPL и выбрали соответствующие значения интенсивности, которые будут использоваться в эксперименте по дискриминации для каждой частоты сравнения. . После того, как были отрегулированы конкретные значения интенсивности для каждой частоты и предмета, и перед заданием по распознаванию частот участники прошли обширную подготовку с визуальной обратной связью, отображаемой на экране компьютера. На начальном этапе обучения мы использовали большие разности частот (> 30 Гц), чтобы познакомить участников с задачей. Во втором тренировочном блоке участники были ознакомлены с меньшей разницей частот (20 ± 2 Гц). Третий обучающий блок был разделен на подблоки, соответствующие каждой базовой частоте, и тесты всегда включали базовую частоту в паре с частотами сравнения ± 8 Гц.Каждый из этих подблоков повторялся до достижения производительности 90%. Затем каждый субблок был повторен еще один или два раза еще раз, непосредственно перед экспериментальным блоком, соответствующим его базовой частоте. Для тестирования каждого человека потребовалось от 5 до 6 часов, и эксперимент был разделен на две сессии. Все экспериментальные блоки проходили в рамках второй сессии.
Просто заметная разница (JND), также известная как порог различия, — это минимальный уровень стимуляции, который человек может обнаружить в 50% случаев.Например, если вас попросили держать два объекта разного веса, просто заметной разницей будет минимальная разница в весе между ними, которую вы можете ощущать в половине случаев.
Важно не путать просто заметную разницу и абсолютный порог. В то время как порог различия включает в себя способность обнаруживать различия в уровнях стимуляции, абсолютный порог относится к наименьшему обнаруживаемому уровню стимуляции.
Абсолютным порогом звука, например, будет наименьший уровень громкости , который может обнаружить человек.Просто заметной разницей будет наименьшее изменение объема , которое может ощутить человек.
Порог различия был впервые описан физиологом и психологом-экспериментатором Эрнстом Вебером, а затем расширен психологом Густавом Фехнером. Закон Вебера, также иногда известный как закон Вебера-Фехнера, предполагает, что просто заметная разница является постоянной пропорцией исходного стимула.
Например, представьте, что вы представили звук участнику, а затем медленно увеличили уровень децибел.Вы должны были увеличить уровень звука на 7 децибел, прежде чем участник мог сказать, что громкость увеличилась. В этом случае просто заметная разница составит 7 децибел. Используя эту информацию, вы могли бы затем использовать закон Вебера, чтобы предсказать просто заметную разницу для других уровней звука.
На самом деле, просто заметная разница может варьироваться в зависимости от испытаний. Вот почему JND обычно определяется путем проведения нескольких испытаний с последующим использованием наименьших уровней, которые участники могут обнаружить, по крайней мере, в 50% случаев.
Уровень интенсивности стимула также может играть роль в том, насколько люди замечают изменения. Если свет очень, очень тусклый, люди могут с большей вероятностью заметить меньшие изменения интенсивности, чем если бы те же самые изменения были внесены в более яркий свет.
Например, представьте, что вы находитесь в темном кинотеатре. Свет в доме начинает медленно включаться, и вы сразу же замечаете даже очень небольшое изменение интенсивности света. После этого вы выходите из театра и выходите на улицу, где ярко светит солнце.Если бы такие же изменения интенсивности света были сделаны снаружи, вы могли бы с меньшей вероятностью их заметить, поскольку уровень стимула намного выше.
Просто заметная разница касается самых разных органов чувств, включая осязание, вкус, обоняние, слух и зрение. Это может относиться, среди прочего, к таким вещам, как яркость, сладость, вес, давление и шум.
Экспериментальное человеческое поведение
участников.
Аппаратура и материалы.
Процедура.
Просто заметная разница (JND) в психологии
Разработка концепции
Примеры
.
