Регрессия (Regression) · Loginom Wiki

Loginom: Логистическая регрессия (обработчик), Линейная регрессия (обработчик)

В теории вероятности и математической статистике это зависимость математического ожидания случайной величины от одной или нескольких других случайных величин.

В отличие от чисто функциональной зависимости y=f(x), где каждому значению независимой переменной x соответствует единственное значение зависимой переменной y, регрессионная зависимость предполагает, что каждому значению переменной x могут соответствовать различные значения y, обусловленные случайной природой зависимости.

Если некоторому значению величины xi соответствует набор значений величин yi1,yi2,…,yin, то зависимость средних арифметических:

¯yi=(yi1,yi2,…,yin)ni

от xi и является регрессией в статистическом понимании данного термина.

Типичным примером регрессионной зависимости может быть зависимость между ростом и весом человека. В большинстве случае вес пропорционален росту, но фактически большой рост не всегда означает большой вес. Иными словами, у роста, например, 175 см. может наблюдаться несколько значений веса, скажем 69, 78 и 86 кг. Тогда зависимость между ростом и средним значением указанных весов будет являться регрессионной.

Изучение регрессии в теории вероятностей основано на том, что случайные величины X и Y, имеющие совместное распределение вероятностей, связаны статистической зависимостью: при каждом фиксированном значении X=x, величина Y является случайной величиной с определённым (зависящим от значения x) условным распределением вероятностей.

Регрессия величины Y по величине X определяется условным математическим ожиданием Y, вычисленным при условии, что X=x:E(Y|x)=u(x).

Уравнение y=u(x) называется уравнением регрессии, а соответствующий график — линией регрессии Y по X. Точность, с которой уравнение Y по X отражает изменение Y в среднем при изменении x, измеряется условной дисперсией D величины Y, вычисленной для каждого значения X=x:D(Y|x)=D(x).

Если D(x)=0 при всех значениях x, то можно достоверно утверждать, что Y и X связаны строгой функциональной зависимостью Y=u(X). Если D(x)=0 при всех значениях x и u(x) не зависит от x, то говорят, что регрессионная зависимость Y по X отсутствует.

Линии регрессии обладают следующим замечательным свойством

: среди всех действительных функций f(X) минимум математического ожидания E[Y—f(X)]2 достигается для функции f(x)=u(X).

Это означает, что регрессия Y по X даёт наилучшее в указанном смысле представление величины Y по величине X. Это свойство позволяет использовать регрессию для предсказания величины Y по X.

Иными словами, если значение Y непосредственно не наблюдается и эксперимент позволяет регистрировать только X, то в качестве прогнозируемого значения Y можно использовать величину Y=u(X).

Наиболее простым является случай, когда регрессионная зависимость Y по X линейна, т.е. E(Y|x)=b0+b1x, где b0 и b1 – коэффициенты регрессии. На практике обычно коэффициенты регрессии в уравнении y=u(x) неизвестны, и их оценивают по наблюдаемым данным.

Регрессия широко используется в аналитических технологиях при решении различных бизнес-задач, таких как прогнозирование (продаж, курсов валют и акций), оценивание различных бизнес-показателей по наблюдаемым значениям других показателей (скоринг), выявление зависимостей между показателями и т.д.

Регрессионный анализ—ArcGIS Insights | Документация

Регрессионный анализ ­ статистический аналитический метод, позволяющий вычислить предполагаемые отношения между зависимой переменной одной или несколькими независимыми переменными. Используя регрессионный анализ, вы можете моделировать отношения между выбранным переменными, а также прогнозируемыми значениями на основе модели.

Обзор регрессионного анализа

Регрессионный анализ использует выбранный метод оценки, зависимую переменную и одну или несколько независимых переменных для создания уравнения, которое оценивает значения зависимой переменной.

Модель регрессии включает выходные данные, например R² и p-значения, по которым можно понять, насколько хорошо модель оценивает зависимую переменную.

Диаграммы, например матрица точечной диаграммы, гистограмма и точечная диаграмма, также используются в регрессионном анализе для анализа отношений и проверки допущений.

Регрессионный анализ используется для решения следующих типов проблем:

• Выявить, какая независимая переменная связана с зависимой.
• Понять отношения между зависимой и независимыми переменными.
• Предсказать неизвестные значения зависимой переменной.

Примеры

Аналитик в рамках исследования для небольшой розничной сети изучает эффективность работы различных магазинов. Он хочет выяснить, почему некоторые магазины показывают очень небольшой объем продаж. Аналитик строит модель регрессии с независимыми переменными, такими как средний возраст и средний доход жителей, проживающих вокруг магазинов, а так же расстояние до торговых центров и остановок общественного транспорта, чтобы выявить, какая именно переменная наиболее влияет на продажи.

Аналитик департамента образования исследует эффективность новой программы питания в школе. Аналитик строит модель регрессии для показателей успеваемости, используя такие независимые переменные, как размер класса, доход семьи, размер подушевого финансирования учащихся и долю учащихся, питающихся в школе. Уравнение модели используется для выявления относительного вклада каждой переменной в показатели успеваемости учебного заведения.

Аналитик неправительственной организации изучает эффект глобальных выбросов парниковых газов. Аналитик строит модель регрессии для выбросов в последнее время, зафиксированных в каждой стране, используя независимые переменные, такие как валовой внутренний продукт( ВВП), численность населения, производство электроэнергии с использованием добываемого углеводородного топлива и использование транспортных средств.

Эту модель можно использовать использована для прогнозирования будущих выбросов парниковых газов на основе предполагаемых значений значений ВВП и численности населения.

Метод наименьших квадратов

Регрессионный анализ в ArcGIS Insights моделируется на основе Метода наименьших квадратов (МНК).

МНК – форма множественной линейной регрессии, допускающей, что отношения между зависимыми и независимыми переменными должны моделироваться подгонкой линейного уравнения к данным наблюдений.

МНК использует следующее уравнение:

yi=β0+β1x1+β2x2+...+βnxn+ε

, где:

• y_i=наблюдаемое=наблюдаемое значение независимой переменной в точке i
• β₀=y-интерсепт (отрезок на координатной оси, постоянное значение)
• β_n=коэффициент регрессии или уклона независимой переменной N в точке i
• x_n=значение переменной N в точке i
• ε=ошибка уравнения регрессии

Допущения (Предположения)

Каждый метод регрессии имеет несколько допущений, которые должны быть выполнены для того, чтобы уравнение считалось надежным. Допущения МНК должны быть проверены при создании модели регрессии.

Следующие допущения должны быть проверены и удовлетворены при использовании метода МНК:

Модель должна быть линейной.

Регрессия МНК используется только при построении линейной модели. Линейную зависимость между зависимой и независимыми переменными можно проверить используя точечную диаграмму (рассеивания). Матрица точечной диаграммы может проверить все переменные, при условии, что всего используется не более 5 переменных.

Данные должны быть распределены произвольно.

Данные, используемые в регрессионном анализе, должны быть произвольно распределены, то есть выборки данных не должны зависеть от какого-либо внешнего фактора. Произвольное распределение можно проверить, используя невязки в модели регрессии. Невязки, рассчитываемые как результат модели регрессии, не должны коррелировать при нанесении их на точечную диаграмму или матрицу точечной диаграммы вместе с независимыми переменными.

Независимые переменные не должны быть коллинеарны.

Коллинеарность — это линейная связь между независимыми переменными, которая создает избыточность в модели. В ряде случаев модель создается с коллинеарностью. Тем не менее, если одна из коллинеарных переменных зависит от другой, возможно, стоит удалить ее из модели. Оценить коллинеарность можно с помощью точечной диаграммы или матрицы точечной диаграммы независимых переменных.

Независимые переменные должны иметь незначительную погрешность измерения.

Точность модели регрессии соответствует точности входных данных. Если независимые переменные имеют большой разброс ошибок, модель нельзя считать точной. При выполнении регрессионного анализа очень важно использовать наборы данных только из известных и доверенных источников, чтобы быть уверенным в незначительности ошибок.

Предполагаемая сумма невязок должна быть равна нулю.

Невязки представляют собой разность между ожидаемыми и наблюдаемыми значениями в регрессионном анализе. Наблюдаемые значения выше кривой регрессии имеют положительное значение невязки, а значения ниже кривой регрессии – отрицательные. Кривая регрессии должны проходить через центр точек данных; соответственно сумма невязок должны стремиться к нулю. Сумму значений поля можно вычислить в суммарной таблице.

Невязки должны иметь равномерную вариабельность.

Величина вариабельности должна быть одинаковой для всех невязок. Это допущение проверяется с использованием точечной диаграммы невязок (ось y) и оцениваемых значений (ось x). Результирующая точечная диаграмма отображается как горизонтальная полоса с произвольно разбросанными точками по всей площади.

Распределение невязок должно соответствовать нормальному.

Нормальное распределение – кривая в форме колокола – является естественным распределением, где высокая частота явления наблюдается рядом со средним значением, и по мере увеличения расстояния от среднего частота снижается. В статистическом анализе нормальное распределение часто используется как нулевая гипотеза. Если распределение невязок соответствует нормальному, линия наилучшего соответствия проходит по центру наблюдаемых точек данных, а не отклоняется, приближаясь к одним, и отклоняясь от других. Это допущение можно проверить, построив гистограмму невязок. Кривая нормального распределения может не поместиться в карточку и сдвиги и эксцессы переносятся на обратную сторону карточки гистограммы.

Смежные невязки не должны обнаруживать автокорреляцию.

Это допущение основано на хронологии данных. Если данные соответствуют хронологии, каждая точка данных должна быть независима от предыдущей или последующей точки данных. Поэтому при выполнении регрессионного анализа важно убедиться, что хронологический порядок данных соответствует нормальному ходу времени. Это допущение вычисляется с использованием теста Дарбина-Уотсона.

Тест Дарбина-Уотсона измеряет автокорреляцию невязок в модели регрессии. Критерий Дурбина-Ватсона использует шкалу от 0 до 4, где значения от 0 до 2 указывают на положительную автокорреляцию, 2 – отсутствие автокорреляции, а от 2 до 4 отрицательную автокорреляцию. То есть, чтобы соответствовать допущению об отсутствии автокорреляции невязок, необходимо получить значение, приближающееся к 2. В целом, значения между 1.5 и 2.5 считаются допустимыми, а меньше 1.5 или больше 2.5 указывают на то, что модель не соответствует утверждению об отсутствии автокорреляции.

Пригодность модели

Точность уравнения регрессии – основа регрессионного анализа. Все модели будут иметь некую ошибку, но понимание этой статистики поможет вам определить, можно ли использовать эту модель для вашего анализа, или необходимо выполнить дополнительные преобразования.

Существуют два метода проверки корректности модели регрессии: исследовательский анализ и подтверждающий анализ.

Исследовательский анализ

Исследовательский анализ – технология анализа данных с использованием разнообразных статистических и визуальных методов. В рамках исследовательского анализа вы проверяете допущения регрессии МНК и сравниваете эффективность различных независимых переменных. Исследовательский анализ позволяет вам сравнить эффективность и точность разных моделей, но не может определить, должны ли вы использовать или отклонить ту или иную модель. Исследовательский анализ необходимо проводить перед анализом подтверждения для каждой модели регрессии, возможно, несколько раз, для сравнения разных моделей.

Как часть исследовательского анализа могут быть использованы следующие диаграммы и статистические показатели:

• Точечная диаграмма (рассеяния) и матрица точечной диаграммы
• Гистограмма и анализ нормального распределения
• Уравнение регрессии и прогнозирование новых наблюдений
• Коэффициент детерминации, R² и скорректированный R²
• Стандартная ошибка невязки
• Точечная диаграмма

Исследовательский анализ начинается, когда вы выбираете независимые переменные, и до построения модели регрессии. Так как МНК – метод линейной регрессии, основное допущение – модель должна быть линейной. Точечная диаграмма (рассеяния) и матрица точечной диаграммы могут быть использованы для анализа линейной зависимости между зависимой переменной и независимыми переменными. Матрица точечной диаграммы может отобразить до 4х независимых переменных с зависимой переменной, что позволяет сразу провести сравнение между всеми переменными. Простая диаграмма рассеяния может отобразить только две переменные: одну зависимую и одну независимую. Просмотр диаграммы рассеяния с зависимой переменной и одной независимой переменной позволяет сделать более точное допущение об отношении между переменными. Линейность можно проверить перед созданием модели регрессии, чтобы определить, какие именно независимые переменные следует использовать для создания пригодной модели.

Несколько выходных статистических показателей также доступны после создания модели регрессии, к ним относятся: уравнение регрессии, значение R² и критерий Дурбина-Ватсона. После создания модели регрессии вы должны использовать выходные показатели, а также диаграммы и таблицы для проверки остальных допущений регрессии МНК. Если ваша модель удовлетворяет допущениям, вы можете продолжить исследовательский анализ.

Уравнение регрессии дает возможность оценить влияние каждой независимой переменной на прогнозируемые значения, включая коэффициент регрессии для каждой независимой переменной. Можно сравнить величины уклона для определения влияния каждой независимой переменной на зависимую переменную; Чем дальше от нуля значение уклона (неважно, в положительную, или отрицательную сторону) – тем больше влияние. Уравнение регрессии также может быть использовано для прогнозирования значений зависимой переменной через вод значений каждой независимой переменной.

Коэффициент детерминации, обозначаемый как R², измеряет, насколько хорошо уравнение регрессии моделирует фактические точки данных. Значение R² – число в диапазоне от 0 до 1, причем, чем ближе значение к 1, тем более точная модель. Если R² равен 1, это указывает на идеальную модель, что крайне маловероятно в реальных ситуациях, учитывая сложность взаимодействий между различными факторами и неизвестными переменными. Поэтому следует стремиться к созданию регрессионной модели с максимально возможным значением R² , понимая, что значение не может быть равно 1.

При выполнении регрессионного анализа существует риск создания модели регрессии, имеющей допустимое значение R², путем добавления независимых переменных, случайным образом показывающих хорошее соответствие. Значение Скорректированный R², которое также должно находиться в диапазоне между 0 и 1, учитывает дополнительные независимые переменные, уменьшая роль случайности в вычислении. Скорректированный R² нужно использовать в модели с большим количеством независимых переменных или при сравнении моделей с различным числом независимых переменных.

Стандартная ошибка невязки измеряет точность, с которой регрессионная модель может предсказывать значения с новыми данными. Меньшие значения указывают на более точную модель, соответственно при сравнении нескольких моделей, та, где это значение самое меньшее из всех – модель, в которой минимизирована стандартная ошибка невязки.

Точечная диаграмма может быть использована для анализа независимых переменных, с целью выявления кластеризации или выбросов, которые могут влиять на точность модели.

Анализ подтверждения

Анализ подтверждения — процесс оценки модели в сравнении с нулевой гипотезой. В регрессионном анализа нулевая гипотеза утверждает, что отношения между зависимой и независимыми переменными отсутствуют. Для модели с отсутствием отношений величина уклона равна 0. Если элементы анализа подтверждения статистически значимы — вы можете отклонить нулевую гипотезу ((другими словами, статистически подтверждается наличие отношений между зависимой и независимыми переменными).

Для определения значимости, как компонента анализа, используются следующие статистические показатели:

• F-статистика, и связанное с ней p-значение
• T-статистика, и связанное с ней p-значение
• Доверительные интервалы

F-статистика — глобальный статистический показатель, возвращаемый F-критерием, который показывает возможности прогнозирования модели через расчет коэффициентов регрессии в модели, которые значительно отличаются от 0. F-критерий анализирует комбинированное влияние независимых переменных, а не оценивает каждую в отдельности. С F-статистикой связано соответствующее p-значение, которое является мерой вероятности того, что детерминированные отношения между переменными являются случайными Так как p-значения базируются на вероятности, значения располагаются в диапазоне от 0. 0 до 1.0. Небольшое p-значение, обычно 0.05 или меньше, свидетельствует о том, что в модели реально есть отношения между переменными (то есть, выявленная закономерность не является случайной) что дает нам право отвергнуть нулевую гипотезу. В этом случае, вероятность того, что отношения в модели случайны, равна 0.05, или 1 к 20. Или, вероятность того, что отношения реальны, равна 0.95, или 19 к 20.

Показатель t-статистика — это локальный статистический показатель, возвращаемый t-критерием, который показывает возможности прогнозирования для каждой независимой переменной отдельно. Так же, как и F-критерий, t-критерий анализирует коэффициенты регрессии в модели, которые значительно отличаются от 0. Так как t-критерий применяется к каждой независимой переменной, модель вернет значение t-статистики для каждой независимой переменной, а не одно значение для всей модели. Каждое значение t-статистики имеет связанное с ним p-значение, которое указывает на значимость независимой переменной. Так же, как и для F-критерия, p-значение для каждого t-критерия должно быть 0.05 или менее, чтобы мы могли отвергнуть нулевую гипотезу. Если p-значение для независимой переменной больше 0.05, эту переменную не стоит включать в модель, и необходимо строить новую модель, даже если глобальное значение вероятности для исходной модели указывает на статистическую значимость.

Доверительные интервалы визуализируют коэффициенты регрессии для каждой независимой переменной и могут быть 90, 95 и 99 процентов. Поэтому доверительные интервалы можно использовать наряду с p-значениями t-критерия для оценки значимости нулевой гипотезы для каждой независимой переменной. Коэффициенты регрессии на должны быть равны 0, только в этом случае вы можете отклонить нулевую гипотезу и продолжить использовать модель. Поэтому, для каждой независимой переменной, коэффициент регрессии, и связанный с ним доверительный интервал не может перекрываться с 0. Если доверительные интервалы в 99 или 95 процентов для данной независимой переменой перекрываются с 0, эта независимая переменная не дает возможности отклонить нулевую гипотезу. Включение этой переменной в модель может негативно повлиять на общую значимость вашей модели. Если только 90-процентный доверительный интервал перекрывается с 0, эта переменная может быть включена в модель, общая статистическая значимость которой вас удовлетворяет. В идеале, доверительные интервалы для всех независимых переменных должны быть как можно дальше от 0.

Другие выходные данные

Остальные выходные данные, такие как прогнозируемые значения и невязки также важны для допущений регрессии МНК. В этом разделе вы можете узнать подробнее, как эти значения вычисляются.

Ожидаемые значения

Ожидаемые значения вычисляются на основе уравнения регрессии и значений каждой независимой переменной. В идеале, ожидаемые значения должны совпадать с наблюдаемыми (реальными значениями зависимой переменной).

Ожидаемые значения, вместе с наблюдаемым значениями, используются для вычисления невязок.

Невязки

Невязки в регрессионном анализе – это различия между наблюдаемыми значениями в наборе данных и ожидаемыми значениями, вычисленными с помощью уравнения регрессии.

Невязки A и B для отношений выше вычисляются следующим образом:

residualsA = observedA - estimatedA residualsA = 595 - 487.62 residualsA = 107.38

residualsB = observedB - estimatedB residualsB = 392 - 527.27 residualsB = -135.27

Невязки используются для вычисления ошибки уравнения регрессии, а также для проверки некоторых допущений.

Основы регрессионного анализа—ArcGIS Pro | Документация

Набор инструментов Пространственная статистика предоставляет эффективные инструменты количественного анализа пространственных структурных закономерностей. Инструмент Анализ горячих точек, например, поможет найти ответы на следующие вопросы:

• Есть ли в США места, где постоянно наблюдается высокая смертность среди молодежи?
• Где находятся «горячие точки» по местам преступлений, вызовов 911 (см. рисунок ниже) или пожаров?
• Где находятся места, в которых количество дорожных происшествий превышает обычный городской уровень?

Анализ данных звонков в службу 911, показывающий горячие точки (красным), холодные точки (синим) и локализацию пожарных/полиции, ответственных за реагирование (зеленые круги)

Каждый из вопросов спрашивает «где»? Следующий логический вопрос для такого типа анализа – «почему»?

• Почему в некоторых местах США наблюдается повышенная смертность молодежи? Какова причина этого?
• Можем ли мы промоделировать характеристики мест, на которые приходится больше всего преступлений, звонков в 911, или пожаров, чтобы помочь сократить эти случаи?
• От каких факторов зависит повышенное число дорожных происшествий? Имеются ли какие-либо возможности для снижения числа дорожных происшествий в городе вообще, и в особо неблагополучных районах в частности?

Инструменты в наборе инструментов Моделирование пространственных отношений помогут вам ответить на вторую серию вопросов «почему». К этим инструментам относятся Метод наименьших квадратов и Географически взвешенная регрессия.

Пространственные отношения

Регрессионный анализ позволяет вам моделировать, проверять и исследовать пространственные отношения и помогает вам объяснить факторы, стоящие за наблюдаемыми пространственными структурными закономерностями. Вы также можете захотеть понять, почему люди постоянно умирают молодыми в некоторых регионах страны, и какие факторы особенно влияют на особенно высокий уровень диабета. При моделирование пространственных отношений, однако, регрессионный анализ также может быть пригоден для прогнозирования. Моделирование факторов, которые влияют на долю выпускников колледжей, на пример, позволяют вам сделать прогноз о потенциальной рабочей силе и их навыках. Вы также можете использовать регрессионный анализ для прогнозирования осадков или качества воздуха в случаях, где интерполяция невозможна из-за малого количества станций наблюдения (к примеру, часто отсутствую измерительные приборы вдоль горных хребтов и в долинах).

МНК – наиболее известный метод регрессионного анализа. Это также подходящая отправная точка для всех способов пространственного регрессионного анализа. Данный метод позволяет построить глобальную модель переменной или процесса, которые вы хотите изучить или спрогнозировать (уровень смертности/осадки). Он создает уравнение регрессии, отражающее происходящий процесс. Географически взвешенная регрессия (ГВР) — один из нескольких методов пространственного регрессионного анализа, все чаще использующегося в географии и других дисциплинах. Метод ГВР (географически взвешенная регрессия) создает локальную модель переменной или процесса, которые вы прогнозируете или изучаете, применяя уравнение регрессии к каждому пространственному объекту в наборе данных. При подходящем использовании, эти методы являются мощным и надежным статистическим средством для проверки и оценки линейных взаимосвязей.

Линейные взаимосвязи могут быть положительными или отрицательными. Если вы обнаружили, что количество поисково-спасательных операций увеличивается при возрастании среднесуточной температуры, такое отношение является положительным; имеется положительная корреляция. Другой способ описать эту положительную взаимосвязь — сказать, что количество поисково-спасательных операций уменьшается при уменьшении среднесуточной температуры. Соответственно, если вы установили, что число преступлений уменьшается при увеличении числа полицейских патрулей, данное отношение является отрицательным. Также, можно выразить это отрицательное отношение, сказав, что количество преступлений увеличивается при уменьшении количества патрулей. На рисунке ниже показаны положительные и отрицательные отношения, а также случаи, когда две переменные не связаны отношениями:

Диаграммы рассеяния: положительная связь, отрицательная связь и пример с 2 не связанными переменными.

Корреляционные анализы, и связанные с ними графики, отображенные выше, показывают силу взаимосвязи между двумя переменными. С другой стороны, регрессионные анализы дают больше информации: они пытаются продемонстрировать степень, с которой 1 или более переменных потенциально вызывают положительные или негативные изменения в другой переменной.

Применения регрессионного анализа

Регрессионный анализ может использоваться в большом количестве приложений:

• Моделирование числа поступивших в среднюю школу для лучшего понимания факторов, удерживающих детей в том же учебном заведении.
• Моделирование дорожных аварий как функции скорости, дорожных условий, погоды и т.д., чтобы проинформировать полицию и снизить несчастные случаи.
• Моделирование потерь от пожаров как функции от таких переменных как степень вовлеченности пожарных департаментов, время обработки вызова, или цена собственности. Если вы обнаружили, что время реагирования на вызов является ключевым фактором, возможно, существует необходимость создания новых пожарных станций. Если вы обнаружили, что вовлеченность – главный фактор, возможно, вам нужно увеличить оборудование и количество пожарных, отправляемых на пожар.

Существует три первостепенных причины, по которым обычно используют регрессионный анализ:

• Смоделировать некоторые явления, чтобы лучше понять их и, возможно, использовать это понимание для оказания влияния на политику и принятие решений о наиболее подходящих действиях. Основная цель — измерить экстент, который при изменениях в одной или более переменных связанно вызывает изменения и в другой. Пример. Требуется понять ключевые характеристики ареала обитания некоторых видов птиц (например, осадки, ресурсы питания, растительность, хищники) для разработки законодательства, направленного на защиту этих видов.
• Смоделировать некоторые явления, чтобы предсказать значения в других местах или в другое время. Основная цель — построить прогнозную модель, которая является как устойчивой, так и точной. Пример: Даны прогнозы населения и типичные погодные условия. Каким будет объем потребляемой электроэнергии в следующем году?
• Вы также можете использовать регрессионный анализ для исследования гипотез. Предположим, что вы моделируете бытовые преступления для их лучшего понимания и возможно, вам удается внедрить политические меры, чтобы остановить их. Как только вы начинаете ваш анализ, вы, возможно, имеете вопросы или гипотезы, которые вы хотите проверить:
  • «Теория разбитого окна» указывает на то, что испорченная общественная собственность (граффити, разрушенные объекты и т.д.) притягивает иные преступления. Имеется ли положительное отношение между вандализмом и взломами в квартиры?
  • Имеется ли связь между нелегальным использованием наркотических средств и взломами в квартиры (могут ли наркоманы воровать, чтобы поддерживать свое существование)?
  • Совершаются ли взломы с целью ограбления? Возможно ли, что будет больше случаев в домохозяйствах с большей долей пожилых людей и женщин?
  • Люди больше подвержены риску ограбления, если они живут в богатой или бедной местности?
  Вы можете использовать регрессионный анализ, чтобы исследовать эти взаимосвязи и ответить на ваши вопросы.

Термины и концепции регрессионного анализа

Невозможно обсуждать регрессионный анализ без предварительного знакомства с основными терминами и концепциями, характерными для регрессионной статистики:

Уравнение регрессии. Это математическая формула, применяемая к независимым переменным, чтобы лучше спрогнозировать зависимую переменную, которую необходимо смоделировать. К сожалению, для тех ученых, кто думает, что х и у это только координаты, независимая переменная в регрессионном анализе всегда обозначается как y, а зависимая – всегда X. Каждая независимая переменная связана с коэффициентами регрессии, описывающими силу и знак взаимосвязи между этими двумя переменными. Уравнение регрессии может выглядеть следующим образом (у – зависимая переменная, Х – независимые переменные, β – коэффициенты регрессии), ниже приводится описание каждого из этих компонентов уравнения регрессии):

Элементы Уравнения регрессии по методу наименьших квадратов

• Зависимая переменная (y) – это переменная, описывающая процесс, который вы пытаетесь предсказать или понять (бытовые кражи, осадки). В уравнении регрессии эта переменная всегда находится слева от знака равенства. В то время, как вы можете использовать регрессию для предсказания зависимой величины, вы всегда начинаете с набора хорошо известных у-значений и используете их для калибровки регрессионной модели. Известные у-значения часто называют наблюдаемыми величинами.
• Независимые переменные (X) это переменные, используемые для моделирования или прогнозирования значений зависимых переменных. В уравнении регрессии они располагаются справа от знака равенства и часто называются независимыми переменными. Зависимая переменная – это функция независимых переменных. Если вас интересует прогнозирование годового оборота определенного магазина, вы можете включить в модель независимые переменные, отражающие, например, число потенциальных покупателей, расстояние до конкурирующих магазинов, заметность магазина и структуру спроса местных жителей.
• Коэффициенты регрессии (β) – это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой. Предположим, что вы моделируете частоту пожаров как функцию от солнечной радиации, растительного покрова, осадков и экспозиции склона. Вы можете ожидать положительную взаимосвязь между частотой пожаров и солнечной радиацией (другими словами, чем больше солнца, тем чаще встречаются пожары). Если отношение положительно, знак связанного коэффициента также положителен. Вы можете ожидать негативную связь между частотой пожаров и осадками (другими словами, для мест с большим количеством осадков характерно меньше лесных пожаров). Коэффициенты отрицательных отношений имеют знак минуса. Когда взаимосвязь сильная, значения коэффициентов достаточно большие (относительно единиц независимой переменной, с которой они связаны). Слабая взаимосвязь описывается коэффициентами с величинами около 0; β₀ – это отрезок, отсекаемый линией регрессии.Он представляет ожидаемое значение зависимой величины, если все независимые переменные равны 0.

P-значения. Большинство регрессионных методов выполняют статистический тест для расчета вероятности, называемой р-значением, для коэффициентов, связанной с каждой независимой переменной. Нулевая гипотеза данного статистического теста предполагает, что коэффициент незначительно отличается от нуля (другими словами, для всех целей и задач, коэффициент равен нулю, и связанная независимая переменная не может объяснить вашу модель). Маленькие величины р-значений отражают маленькие вероятности и предполагают, что коэффициент действительно важен для вашей модели со значением, существенно отличающимся от 0 (другими словами, маленькие величины р-значений свидетельствуют о том, что коэффициент не равен 0). Вы бы сказали, что коэффициент с р-значением, равным 0,01, например, статистически значимый для 99 % доверительного интервала; связанные переменные являются эффективным предсказателем. Переменные с коэффициентами около 0 не помогают предсказать или смоделировать зависимые величины; они практически всегда удаляются из регрессионного уравнения, если только нет веских причин сохранить их.

R²/R-квадрат: Статистические показатели составной R-квадрат и скорректированный R-квадрат вычисляются из регрессионного уравнения, чтобы качественно оценить модель. Значение R-квадрат лежит в пределах от 0 до 100 процентов. Если ваша модель описывает наблюдаемые зависимые переменные идеально, R-квадрат равен 1.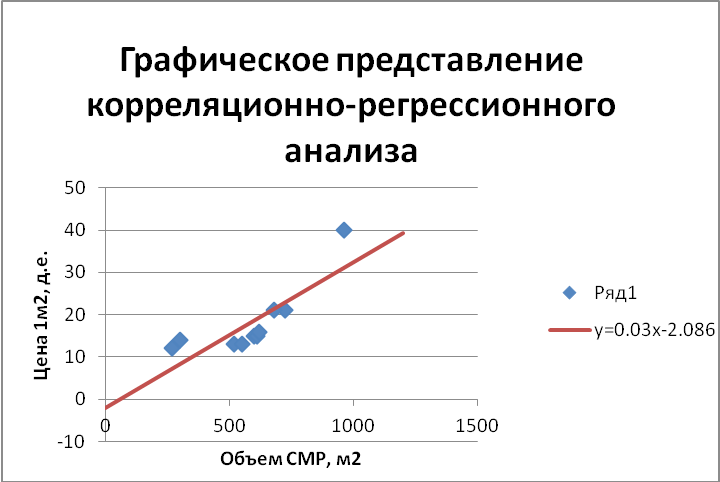 0 (и вы, несомненно, сделали ошибку; возможно, вы использовали модификацию величины у для предсказания у). Вероятнее всего, вы увидите значения R-квадрат в районе 0,49, например, вы можете интерпретировать подобный результат как «Это модель объясняет 49 % вариации зависимой величины». Чтобы понять, как работает R-квадрат, постройте график, отражающий наблюдаемые и оцениваемые значения у, отсортированные по оцениваемым величинам. Обратите внимание на количество совпадений. Этот график визуально отображает, насколько хорошо вычисленные значения модели объясняют изменения наблюдаемых значений зависимых переменных. Просмотрите иллюстрацию. Скорректированный R-квадрат всегда немного меньше, чем множественный R-квадрат, т.к. он отражает всю сложность модели (количество переменных) и связан с набором исходных данных. Следовательно, скорректированный R-квадрат является более точной мерой для оценки результатов работы модели.

Невязки: Существует необъяснимое количество зависимых величин, представленных в уравнении регрессии как случайные ошибки ε. См. рисунок. Известные значения зависимой переменной используются для построения и настройки модели регрессии. Используя известные величины зависимой переменной (Y) и известные значений для всех независимых переменных (Хs), регрессионный инструмент создаст уравнение, которое предскажет те известные у-значения как можно лучше. Однако предсказанные значения редко точно совпадают с наблюдаемыми величинами. Разница между наблюдаемыми и предсказываемыми значениями у называется невязка или отклонение. Величина отклонений регрессионного уравнения — одно из измерений качества работы модели. Большие отклонения говорят о ненадлежащем качестве модели.

Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных, чтобы объяснить зависимые переменные, которые вы пытаетесь смоделировать или понять, запуская инструмент регрессии, чтобы определить, какие величины являются эффективными предсказателями. Затем пошаговое удаление и/или добавление переменных до тех пор, пока вы не найдете наилучшим образом подходящую регрессионную модель. Т.к. процесс создания модели часто исследовательский, он никогда не должен становиться простым «подгоном» данных. Он должен учитывать теоретические аспекты, мнение экспертов в этой области и здравый смысл. Вы должным быть способны определить ожидаемую взаимосвязь между каждой потенциальной независимой переменной и зависимой величиной до непосредственного анализа, и должны задать себе дополнительные вопросы, когда эти связи не совпадают.

Особенности регрессионного анализа

Регрессия МНК – это простой метод анализа с хорошо проработанной теорией, предоставляющий эффективные возможности диагностики, которые помогут вам интерпретировать результаты и устранять неполадки. Однако, МНК надежен и эффективен, если ваши данные и регрессионная модель удовлетворяют всем предположениям, требуемым для этого метода (смотри таблицу внизу). Пространственные данные часто нарушают предположения и требования МНК, поэтому важно использовать инструменты регрессии в союзе с подходящими инструментами диагностики, которые позволяют оценить, является ли регрессия подходящим методом для вашего анализа, а приведенная структура данных и модель может быть применена.

Как регрессионная модель может не работать

Серьезной преградой для многих регрессионных моделей является ошибка спецификации. Модель ошибки спецификации — это такая неполная модель, в которой отсутствуют важные независимые переменные, поэтому она неадекватно представляет то, что мы пытаемся моделировать или предсказывать (зависимую величину, у). Другими словами, регрессионная модель не рассказывает вам всю историю. Ошибка спецификации становится очевидной, когда в отклонениях вашей регрессионной модели наблюдается статистически значимая пространственная автокорреляция, или другими словами, когда отклонения вашей модели кластеризуются в пространстве (недооценки – в одной области изучаемой территории, а переоценки – в другой). Благодаря картографированию отклонений регрессии или коэффициентов, связанных с географически взвешенной регрессией, вы сможете обратить ваше внимание на какие-то нюансы, которые вы упустили ранее. Запуск Анализа горячих точек по отклонениям регрессии также может раскрыть разные пространственные режимы, которые можно моделировать при помощи метода наименьших квадратов с региональными показателями или исправлять с использованием географически взвешенной регрессии. Предположим, когда вы картографируете отклонения вашей регрессионной модели, вы видите, что модель всегда заново предсказывает значения в горах, и, наоборот, в долинах, что может значить, что отсутствуют данные о рельефе. Однако может случиться так, что отсутствующие переменные слишком сложны для моделирования или их невозможно подсчитать или слишком трудно измерить. В этих случаях, вы можете воспользоваться ГВР (географически взвешенной регрессией) или другой пространственной регрессией, чтобы получить хорошую модель.

В следующей таблице перечислены типичные проблемы с регрессионными моделями и инструменты в ArcGIS:

Типичные проблемы с регрессией, последствия и решения

Типичные проблемы с регрессией и их решения

Ошибки спецификации относительно независимых переменных.	Когда ключевые независимые переменные отсутствуют в регрессионном анализе, коэффициентам и связанным с ними р-значениям нельзя доверять.	Создайте карту и проверьте невязки МНК и коэффициенты ГВР или запустите Анализ горячих точек по регрессионным невязкам МНК, чтобы увидеть, насколько это позволяет судить о возможных отсутствующих переменных.
Нелинейные взаимосвязи. Просмотрите иллюстрацию.	МНК и ГВР – линейные методы. Если взаимосвязи между любыми независимыми величинами и зависимыми – нелинейны, результирующая модель будет работать плохо.	Создайте диаграмму рассеяния, чтобы выявить взаимосвязи между показателями в модели.Уделите особое внимание взаимосвязям, включающим зависимые переменные. Обычно криволинейность может быть устранена трансформированием величин. Просмотрите иллюстрацию. Альтернативно, используйте нелинейный метод регрессии.
Выбросы данных. Просмотрите иллюстрацию.	Существенные выбросы могут увести результаты взаимоотношений регрессионной модели далеко от реальности, внося ошибку в коэффициенты регрессии.	Создайте диаграмму рассеяния и другие графики (гистограммы), чтобы проверить экстремальные значения данных. Скорректировать или удалить выбросы, если они представляют ошибки. Когда выбросы соответствуют действительности, они не могут быть удалены. Запустить регрессию с и без выбросов, чтобы оценить, как это влияет на результат.
Нестационарность. Вы можете обнаружить, что входящая переменная, может иметь сильную зависимость в регионе А, и в то время быть незначительной или даже поменять знак в регионе B (см. рисунок).	Если взаимосвязь между вашими зависимыми и независимыми величинами противоречит в пределах вашей области изучения, рассчитанные стандартные ошибки будут искусственно раздуты.	Инструмент МНК в ArcGIS автоматически тестирует проблемы, связанные с нестационарностью (региональными вариациями) и вычисляет устойчивые стандартные значения ошибок. Просмотрите иллюстрацию. Когда вероятности, связанные с тестом Koenker, малы (например, < 0,05), у вас есть статистически значимая региональная вариация и вам необходимо учитывать устойчивые вероятности, чтобы определить, является ли независимая переменная статистически значимой или нет. Как правило, результаты моделирования можно улучшить с помощью инструмента Географически взвешенная регрессия.
Мультиколлинеарность. Одна или несколько независимых переменных излишни. Просмотрите иллюстрацию.	Мультиколлинеарность ведет к переоценке и нестабильной/ненадежной модели.	Инструмент МНК в ArcGIS автоматически проверяет избыточность. Каждой независимой переменной присваивается рассчитанная величина фактора, увеличивающего дисперсию. Когда это значение велико (например, > 7,5), избыток является проблемой и излишние показатели должны быть удалены из модели или модифицированы путем создания взаимосвязанных величин или увеличением размера выборки. Просмотрите иллюстрацию.
Противоречивая вариация в отклонениях. Может произойти, что модель хорошо работает для маленьких величин, но становится ненадежна для больших значений. Просмотрите иллюстрацию.	Когда модель плохо предсказывает некоторые группы значений, результаты будут носить ошибочный характер.	Инструмент МНК в ArcGIS автоматически выполняет тест на несистемность вариаций в отклонениях (называемая гетероскедастичность или неоднородность дисперсии) и вычисляет стандартные ошибки, которые устойчивы к этой проблеме. Когда вероятности, связанные с тестом Koenker, малы (например, 0,05), необходимо учитывать устойчивые вероятности, чтобы определить, является ли независимая переменная статистически значимой или нет. Просмотрите иллюстрацию.
Пространственно автокоррелированные отклонения. Просмотрите иллюстрацию.	Когда наблюдается пространственная кластеризация в отклонениях, полученных в результате работы модели, это означает, что имеется переоценённый тип систематических отклонений, модель работает ненадежно.	Запустите инструмент Пространственная автокорреляция (Spatial Autocorrelation) по отклонениям, чтобы убедиться, что в них не наблюдается статистически значимой пространственной автокорреляции. Статистически значимая пространственная автокорреляция практически всегда является симптомом ошибки спецификации (отсутствует ключевой показатель в модели). Просмотрите иллюстрацию.
Нормальное распределение систематической ошибки. Просмотрите иллюстрацию.	Когда невязки регрессионной модели распределены ненормально со средним, близким к 0, р-значения, связанные с коэффициентами, ненадежны.	Инструмент МНК в ArcGIS автоматически выполняет тест на нормальность распределения отклонений. Когда статистический показатель Жака-Бера является значимым (например, 0,05), скорее всего в вашей модели отсутствует ключевой показатель (ошибка спецификации) или некоторые отношения, которые вы моделируете, являются нелинейными. Проверьте карту отклонений и возможно карту с коэффициентами ГВР, чтобы определить, какие ключевые показатели отсутствуют. Просмотр диаграмм рассеяния и поиск нелинейных отношений.

Важно протестировать модель на каждую из проблем, перечисленных выше. Результаты могут быть на 100 % неправильны, если игнорируются проблемы, упомянутые выше.

Пространственная регрессия

Для пространственных данных характерно 2 свойства, которые затрудняют (не делают невозможным) применение традиционных (непространственных) методов, таких как МНК:

• Географические объекты довольно часто пространственно автокоррелированы. Это означает, что объекты, расположенные ближе друг к другу более похожи между собой, чем удаленные объекты. Это создает переоцененный тип систематических ошибок для традиционных моделей регрессии.
• География важна, и часто наиболее важные процессы нестационарны. Эти процессы протекают по-разному в разных частях области изучения. Эта характеристика пространственных данных может относиться как к региональным вариациям, так и к нестационарности.

Настоящие методы пространственной регрессии были разработаны, чтобы устойчиво справляться с этими двумя характеристиками пространственных данных и даже использовать эти свойства пространственных данных, чтобы улучшать моделирование взаимосвязей. Некоторые методы пространственной регрессии эффективно имеют дело с 1 характеристикой (пространственная автокорреляция), другие – со второй (нестационарность). В настоящее время, нет методов пространственной регрессии, которые эффективны с обеими характеристиками. Для правильно настроенной модели ГВР пространственная автокорреляция обычно не является проблемой.

Пространственная автокорреляция

Существует большая разница в том, как традиционные и пространственные статистические методы смотрят на пространственную автокорреляцию. Традиционные статистические методы видят ее как плохую вещь, которая должна быть устранена, т.к. пространственная автокорреляция ухудшает предположения многих традиционных статистических методов. Для географа или ГИС-аналитика, однако, пространственная автокорреляция является доказательством важности пространственных процессов; это интегральная компонента данных. Удаляя пространство, мы удаляем пространственный контекст данных; это как только половина истории. Пространственные процессы и доказательство пространственных взаимосвязей в данных представляют собой особый интерес, и поэтому пользователи ГИС с радостью используют инструменты пространственного анализа данных. Однако, чтобы избежать переоцененный тип систематических ошибок в вашей модели, вы должны определить полный набор независимых переменных, которые эффективно опишут структуру ваших данных. Если вы не можете определить все эти переменные, скорее всего, вы увидите существенную пространственную автокорреляцию среди отклонений модели. К сожалению, вы не можете доверять результатам регрессии, пока все не устранено. Используйте инструмент Пространственная автокорреляция, чтобы выполнить тест на статистически значимую пространственную автокорреляцию для отклонений в вашей регрессии.

Как минимум существует 3 направления, как поступать с пространственной автокорреляцией в невязках регрессионных моделей.

1. Изменять размер выборки до тех пор, пока не удастся устранить статистически значимую пространственную автокорреляцию. Это не гарантирует, что в анализе будет полностью устранена проблема пространственной автокорреляции, но она значительно меньше, когда пространственная автокорреляция удалена из зависимых и независимых переменных. Это традиционный статистический подход к устранению пространственной автокорреляции и только подходит, если пространственная автокорреляция является результатом избыточности данных.
2. Изолируйте пространственные и непространственные компоненты каждой входящей величины, используя методы фильтрации в пространственной регрессии. Пространство удалено из каждой величины, но затем его возвращают обратно в регрессионную модель в качестве новой переменной, отвечающей за пространственные эффекты/пространственную структуру. ArcGIS в настоящее время не предоставляет возможности проведения подобного рода анализа.
3. Внедрите пространственную автокорреляцию в регрессионную модель, используя пространственные эконометрические регрессионные модели. Пространственные эконометрические регрессионные модели будут добавлены в ArcGIS в следующем релизе.

Региональные вариации

Глобальные модели, подобные МНК, создают уравнения, наилучшим образом описывающие общие связи в данных в пределах изучаемой территории. Когда те взаимосвязи противоречивы в пределах территории изучения, МНК хорошо моделирует эти взаимосвязи. Когда те взаимосвязи ведут себя по-разному в разных частях области изучения, регрессионное уравнение представляет средние результаты, и в случае, когда те взаимосвязи представляют 2 экстремальных значения, глобальное среднее не моделирует хорошо эти значения. Когда ваши независимые переменные испытывают нестационарность (региональные вариации), глобальные модели не подходят, а необходимо использовать устойчивые методы регрессионного анализа. Идеально, вы сможете определить полный набор независимых переменных, чтобы справиться с региональными вариациями в ваших зависимых переменных. Если вы не сможете определить все пространственные переменные, вы снова заметите статистически значимую пространственную автокорреляцию в ваших отклонениях и/или более низкие, чем ожидалось, значения R-квадрат. К сожалению, вы не можете доверять результатам регрессии, пока все не устранено.

Существует как минимум 4 способа работы с региональными вариациями в МНК регрессионных моделях:

1. Включить переменную в модель, которая объяснит региональные вариации. Если вы видите, что ваша модель всегда «перепредсказывает» на севере и «недопредсказывает» на юге, добавьте набор региональных значений:1 для северных объектов, и 0 для южных объектов.
2. Используйте методы, которые включают региональные вариации в регрессионную модель, такие как Географически взвешенная регрессия.
3. Примите во внимание устойчивые стандартные отклонения регрессии и вероятности, чтобы определить, являются ли коэффициенты статистически значимыми. ГВР рекомендуется
4. Изменить/сократить размер области изучения так, чтобы процессы в пределах новой области изучения были стационарными (не испытывали региональные вариации).

Дополнительные ресурсы

Для большей информации по использованию регрессионных инструментов, см.:

Связанные разделы

---

Отзыв по этому разделу?

5 видов регрессии и их свойства. При помощи построения регрессионных… | by Margarita M | NOP::Nuances of Programming

Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.

Мы познакомимся с 7 наиболее распространенными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

Где a_n — это коэффициенты, X_n — переменные и b — смещение. Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!

Иллюстрация поиска оптимальных параметром для линейной регрессии с помощью градиентного спуска

Несколько важных пунктов о линейной регрессии:

• Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
• Обозначения интуитивно-понятны.
• Чувствительна к выбросам.

Полиномиальная регрессия

Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:

Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b

У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.

Линейная и полиномиальная регрессии с нелинейно разделенными данными

Несколько важных пунктов о полиномиальной регрессии:

• Моделирует нелинейно разделенные данные (чего не может линейная регрессия). Она более гибкая и может моделировать сложные взаимосвязи.
• Полный контроль над моделированием переменных объекта (выбор степени).
• Необходимо внимательно создавать модель. Необходимо обладать некоторыми знаниями о данных, для выбора наиболее подходящей степени.
• При неправильном выборе степени, данная модель может быть перенасыщена.

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

• Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
• При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
• Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

min || Xw — y ||²

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

min || Xw — y ||² + z|| w ||²

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

• Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
• Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

min || Xw — y ||² + z|| w ||

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

• Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
• Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
• Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.

Регрессия «эластичная сеть»

Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.

min || Xw — y ||² + z_1|| w || + z_2|| w ||²

Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.

Несколько важных пунктов о регрессии эластичной сети:

• Она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как метод лассо.
• Нет ограничений по количеству выбранных переменных.

Вывод

Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.

Перевод статьи George Seif: 5 Types of Regression and their properties

Парная линейная регрессия. Задачи регрессионного анализа

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины

y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

y = ax + 

b,

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена

линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

где

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.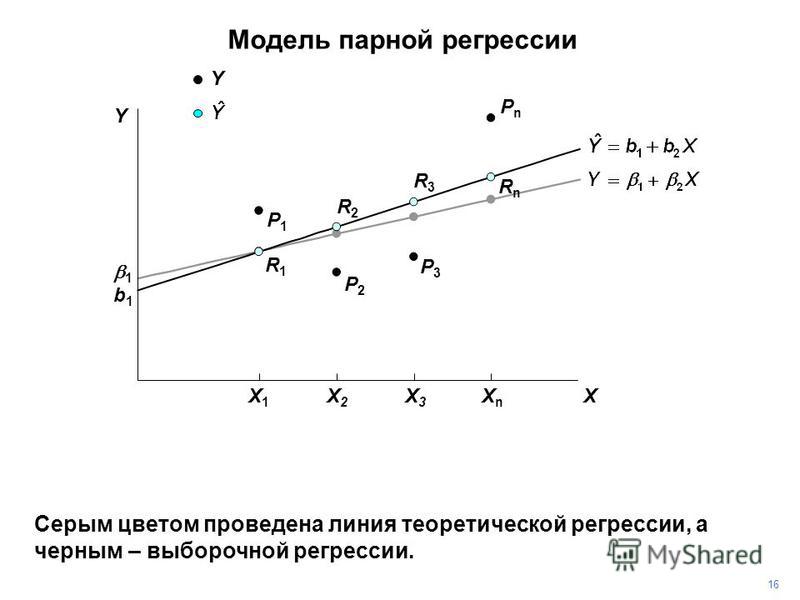

Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

или

где

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа  , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X  и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

---

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Правильное решение и ответ.

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

где

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

Правильное решение и ответ.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

где

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593, SSE = 10 459,587, SSR = 53 311,007.

Можем убедиться, что выполняется закономерность SSR = SST — SSE:

63770,593-10459,587=53311,007.

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии .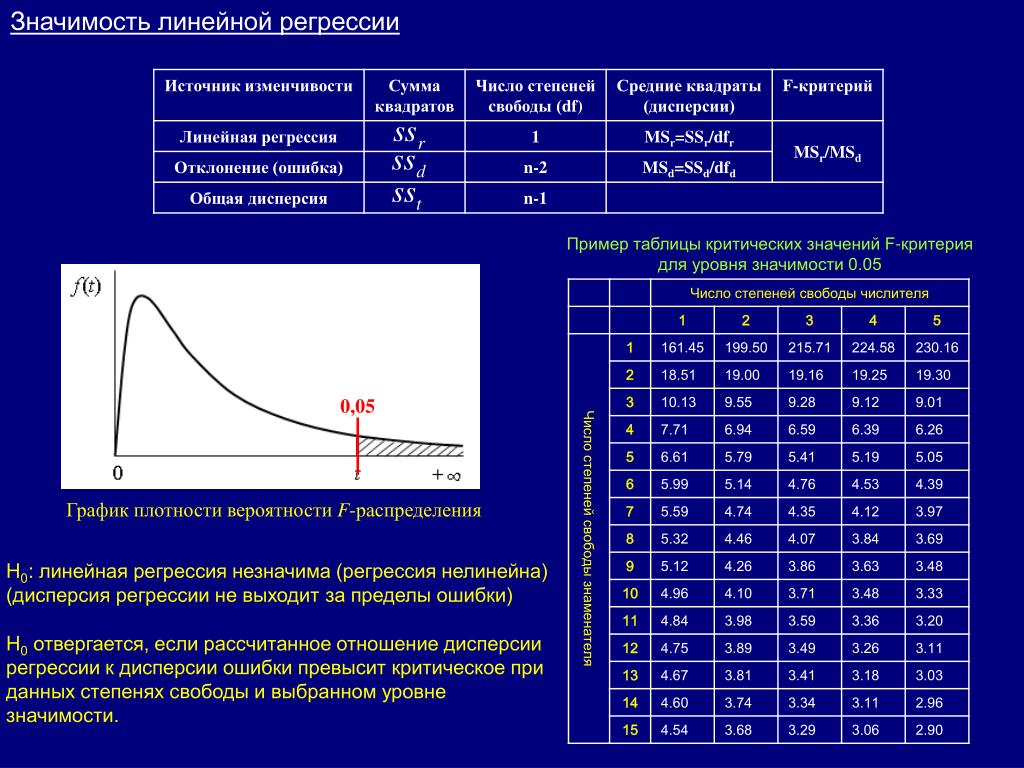 Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии xi = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. yi = 17036,4662.

Подставляем в уравнение парной линейной регрессии xi = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. yi = 4161,9662.

Если доход не меняется, то xi = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

• установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
• выявление причинных связей между переменными величинами;
• прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.

Нулевую гипотезу

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2,

где — стандартная погрешность коэффициента направления прямой линейной регресии b1.

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b1:

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.

Всё по теме «Математическая статистика»

Статистика — Линейная регрессия — CoderLessons.com

После того, как степень взаимосвязи между переменными была установлена ​​с использованием анализа взаимосвязи, естественно, углубиться в природу взаимосвязи. Регрессионный анализ помогает определить причинно-следственную связь между переменными. Можно предсказать значение других переменных (называемых зависимой переменной), если значения независимых переменных можно предсказать с помощью графического метода или алгебраического метода.

Графический метод

Он включает в себя построение диаграммы рассеяния с независимой переменной на оси X и зависимой переменной на оси Y. После этого линия рисуется таким образом, что она проходит через большую часть распределения, а оставшиеся точки распределены почти равномерно по обе стороны от линии.

Линия регрессии известна как линия наилучшего соответствия, которая суммирует общее движение данных. Он показывает наилучшие средние значения одной переменной, соответствующие средним значениям другой. Линия регрессии основана на критериях того, что это прямая линия, которая минимизирует сумму квадратов отклонений между прогнозируемыми и наблюдаемыми значениями зависимой переменной.

Алгебраический метод

Алгебраический метод строит два уравнения регрессии X на Y и Y на X.

Уравнение регрессии Y на X

Y=a+bX

Где —

• Y = Зависимая переменная

• X = Независимая переменная

• a = Константа, показывающая Y-перехват

• b = Константа, показывающая наклон линии

Y = Зависимая переменная

X = Независимая переменная

a = Константа, показывающая Y-перехват

b = Константа, показывающая наклон линии

Значения a и b получают с помощью следующих нормальных уравнений:

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2

Где —

N = Количество наблюдений

Уравнение регрессии X на Y

X=a+bY

Где —

• X = Зависимая переменная

• Y = Независимая переменная

• a = Константа, показывающая Y-перехват

• b = Константа, показывающая наклон линии

X = Зависимая переменная

Y = Независимая переменная

a = Константа, показывающая Y-перехват

b = Константа, показывающая наклон линии

Значения a и b получают с помощью следующих нормальных уравнений:

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2

Где —

N = Количество наблюдений

пример

Постановка задачи:

Исследователь обнаружил, что существует взаимосвязь между весовыми тенденциями отца и сына. В настоящее время он заинтересован в разработке уравнения регрессии по двум переменным по приведенным данным:

Вес отца (в кг)	69	63	66	64	67	64	70	66	68	67	65	71
Вес сына (в кг)	70	65	68	65	69	66	68	65	71	67	64	72

развивать

1. Уравнение регрессии Y на X.

2. Уравнение регрессии по Y.

Уравнение регрессии Y на X.

Уравнение регрессии по Y.

Решение:

X	X2	Y	Y2	XY
69	4761	70	4900	4830
63	3969	65	4225	4095
66	4356	68	4624	4488
64	4096	65	4225	4160
67	4489	69	4761	4623
64	4096	66	4356	4224
70	4900	68	4624	4760
66	4356	65	4225	4290
68	4624	71	5041	4828
67	4489	67	4489	4489
65	4225	64	4096	4160
71	5041	72	5184	5112
sumX=800	sumX2=53,402	sumY=810	sumY2=54750	sumXY=54,059

Уравнение регрессии Y на X

Y = a + bX

Где a и b получены нормальными уравнениями

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2[7pt]Где  sumY=810, sumX=800, sumX2=53,402[7pt], sumXY=54,049,N=12

 Rightarrow 810 = 12a + 800b … (i)

 Rightarrow 54049 = 800a + 53402 b … (ii)

 Rightarrow 810 = 12a + 800b … (i)

 Rightarrow 54049 = 800a + 53402 b … (ii)

Умножив уравнение (i) на 800 и уравнение (ii) на 12, получим:

96000 a + 640000 b = 648000 … (iii)

96000 + 640824 b = 648588 … (iv)

96000 a + 640000 b = 648000 … (iii)

96000 + 640824 b = 648588 … (iv)

Вычитая уравнение (iv) из (iii)

-824 b = -588

 Rightarrow b = -.0713

-824 b = -588

 Rightarrow b = -.0713

Подставляя значение b в уравнение (я)

810 = 12a + 800 (-0,713)

810 = 12а + 570,4

12а = 239,6

 Rightarrow a = 19,96

810 = 12a + 800 (-0,713)

810 = 12а + 570,4

12а = 239,6

 Rightarrow a = 19,96

Следовательно, уравнение Y на X можно записать в виде

Y=19,96−0,713X

Уравнение регрессии Y на X

X = a + bY

Где a и b получены нормальными уравнениями

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2[7pt]Где  sumY=810, sumY2=54750[7pt], sumXY=54,049,N=12

 Rightarrow 800 = 12a + 810a + 810b … (V)

 Rightarrow 54 049 = 810a + 54 750 … (vi)

 Rightarrow 800 = 12a + 810a + 810b … (V)

 Rightarrow 54 049 = 810a + 54 750 … (vi)

Умножив eq (v) на 810 и eq (vi) на 12, получим

9720 a + 656100 b = 648000 … (vii)

9720 + 65700 b = 648588 … (viii)

9720 a + 656100 b = 648000 … (vii)

9720 + 65700 b = 648588 … (viii)

Вычитание из формулы из уравнения

900b = -588

 Rightarrow b = 0,653

900b = -588

 Rightarrow b = 0,653

Подставляя значение b в уравнение (v)

800 = 12а + 810 (0,653)

12а = 271,07

 Rightarrow a = 22,58

800 = 12а + 810 (0,653)

12а = 271,07

 Rightarrow a = 22,58

Следовательно, уравнение регрессии X и Y

Методы статистики

Критерии и методы

Парная линейная регрессия является одним из наиболее простых и надежных способов описать зависимость одного количественного показателя от другого, тоже количественного.

В результате применения метода мы получаем уравнение следующего вида:

Y = A·X + B,

где Y — зависимый количественный показатель, X — независимый количественный показатель, А — коэффициент регрессии, В — константа.

Парная линейная регрессия относится к методам построения прогностической модели, которой, по сути, и является указанное уравнение. То есть мы получаем возможность прогнозировать показатель Y, если нам известно значение показателя X.

Какой смысл имеют коэффициенты А и В?
• Коэффициент регрессии А показывает, на сколько увеличится прогнозируемое значение Y, при увеличении X на 1 единицу.
• Константа В равна ожидаемому значению показателя Y при X=0.

Также принято представлять результаты парной линейной регрессии в виде диаграммы рассеяния, которая строится в обычной двумерной системе координат со шкалами абсцисс (Х) и ординат (Y). Диаграмма состоит из линии, соответствующей функции Y=A•X+B, и множества точек, координаты каждой из которых соответствуют значениям показателей X и Y у конкретного пациента.

Ниже представлен пример диаграммы рассеяния, описывающей прямую зависимость систолического артериального давления от индекса массы тела пациентов.

Например, с помощью метода парной линейной регрессии разработана модель для прогнозирования массы ребёнка в возрасте до 1 года (Y), исходя из его возраста в месяцах (X). В результате получено следующее уравнение регрессии:

Y = 0,5·X + 3,3,

где Y — масса ребёнка в кг, Х — возраст в мес., A=0.5 показывает, что при увеличении возраста на 1 мес. масса увеличится в среднем на 0.5 кг, В=3.3 показывает, что средняя масса ребёнка при рождении (Х=0) составляет 3.3 кг.

Если мы хотим рассчитать массу 8-месячного малыша, подставляем 8 вместо Х и получаем:

Y = 0,5·8 + 3,3 = 7,3 кг

Определение регрессии

Что такое регресс?

Регрессия — это статистический метод, используемый в финансах, инвестициях и других дисциплинах, который пытается определить силу и характер связи между одной зависимой переменной (обычно обозначаемой Y) и рядом других переменных (известных как независимые переменные).

Регрессия помогает инвестиционным и финансовым менеджерам оценивать активы и понимать взаимосвязь между переменными, такими как цены на товары и акции компаний, торгующих этими товарами.

Объяснение регрессии

Два основных типа регрессии — это простая линейная регрессия и множественная линейная регрессия, хотя существуют методы нелинейной регрессии для более сложных данных и анализа. Простая линейная регрессия использует одну независимую переменную для объяснения или предсказания результата зависимой переменной Y, тогда как множественная линейная регрессия использует две или более независимых переменных для предсказания результата.

Регрессия может помочь профессионалам в области финансов и инвестиций, а также специалистам в других сферах бизнеса.Регрессия также может помочь спрогнозировать продажи компании на основе погоды, предыдущих продаж, роста ВВП или других типов условий. Модель ценообразования капитальных активов (CAPM) — это часто используемая регрессионная модель в финансах для определения стоимости активов и определения стоимости капитала.

Общая форма каждого типа регрессии:

• Простая линейная регрессия: Y = a + bX + u
• Множественная линейная регрессия: Y = a + b ₁ X ₁ ⁺ b ₂ X ₂ + b ₃ X ₃ +… + b _т X _т + u

Где:

• Y = переменная, которую вы пытаетесь предсказать (зависимая переменная).
• X = переменная, которую вы используете для прогнозирования Y (независимая переменная).
• a = перехват.
• b = наклон.
• u = остаток регрессии.

Существует два основных типа регрессии: простая линейная регрессия и множественная линейная регрессия.

Регрессия берет группу случайных величин, которые, как считается, предсказывают Y, и пытается найти математическую связь между ними.Эта связь обычно имеет форму прямой линии (линейная регрессия), которая наилучшим образом аппроксимирует все отдельные точки данных. При множественной регрессии отдельные переменные различаются с помощью индексов.

Ключевые выводы

• Регрессия помогает инвестиционным и финансовым менеджерам оценивать активы и понимать взаимосвязи между переменными
• Regression может помочь профессионалам в области финансов и инвестиций, а также специалистам в других сферах бизнеса.

Реальный пример использования регрессионного анализа

Регрессия часто используется для определения того, сколько конкретных факторов, таких как цена товара, процентные ставки, конкретные отрасли или секторы, влияют на движение цены актива. Вышеупомянутый CAPM основан на регрессии и используется для прогнозирования ожидаемой доходности акций и для определения стоимости капитала. Доходность акции сравнивается с доходностью более широкого индекса, такого как S&P 500, для создания бета-версии для конкретной акции.

Бета — это риск акции по отношению к рынку или индексу и отражается как наклон в модели CAPM. Доходность рассматриваемой акции будет зависимой переменной Y, а независимая переменная X — премией за рыночный риск.

Дополнительные переменные, такие как рыночная капитализация акций, коэффициенты оценки и недавняя доходность, могут быть добавлены в модель CAPM, чтобы получить более точные оценки доходности. Эти дополнительные факторы известны как факторы Фама-Френча, названные в честь профессоров, которые разработали модель множественной линейной регрессии для лучшего объяснения доходности активов.Взаимодействие с другими людьми

Пошаговых статей, видео и простых определений

Вероятность и статистика> Регрессионный анализ

Простой график линейной регрессии для количества осадков.

Регрессионный анализ — это способ найти тенденции в данных. Например, вы можете предположить, что существует связь между тем, сколько вы едите и сколько вы весите; регрессионный анализ может помочь вам количественно оценить это.

Регрессионный анализ предоставит вам уравнение для графика, чтобы вы могли делать прогнозы относительно ваших данных.Например, если вы прибавляли в весе в течение последних нескольких лет, он может предсказать, сколько вы будете весить через десять лет, если продолжите набирать вес с той же скоростью. Он также предоставит вам множество статистических данных (включая значение p и коэффициент корреляции), чтобы узнать, насколько точна ваша модель. Большинство курсов по элементарной статистике охватывают самые базовые методы, такие как построение диаграмм рассеяния и выполнение линейной регрессии. Однако вы можете встретить более сложные методы, такие как множественная регрессия.

В комплекте:

1. Введение в регрессионный анализ
2. Множественный регрессионный анализ
3. Переоснащение и как этого избежать
4. Статьи по теме

Технологии:

1. Регресс в Minitab

В статистике трудно смотреть на набор случайных чисел в таблице и пытаться разобраться в этом. Например, глобальное потепление может снизить среднее количество снегопадов в вашем городе, и вас просят предсказать, сколько снега, по вашему мнению, выпадет в этом году.Глядя на следующую таблицу, вы можете предположить, что где-то около 10-20 дюймов. Это хорошее предположение, но вы можете сделать лучше, чем , используя регрессию.

По сути, регрессия — это «лучшее предположение» при использовании набора данных для какого-либо прогноза. Это подгонка набора точек к графику. Существует целый ряд инструментов, которые могут запускать регрессию для вас, включая Excel, который я использовал здесь, чтобы помочь разобраться в данных о снегопадах:

Просто взглянув на линию регрессии, проходящую через данные, вы можете точно настроить все, что вам нужно. угадай немного.Вы можете видеть, что первоначальное предположение (20 дюймов или около того) было неверным. В 2015 году линия будет составлять от 5 до 10 дюймов! Это может быть «достаточно хорошо», но регрессия также дает вам полезное уравнение, которое для этого графика выглядит следующим образом:
y = -2,2923x + 4624,4.
Это означает, что вы можете ввести значение x (год) и получить довольно хорошую оценку количества снегопадов для любого года. Например, 2005 год:
y = -2,2923 (2005) + 4624,4 = 28,3385 дюйма, что довольно близко к фактическому значению 30 дюймов для этого года.

Лучше всего то, что вы можете использовать уравнение для прогнозов. Например, сколько снега выпадет в 2017 году?
y = 2,2923 (2017) + 4624,4 = 0,8 дюйма.

Регрессия также дает значение R в квадрате, которое для этого графика составляет 0,702. Этот номер говорит вам, насколько хороша ваша модель. Значения варьируются от 0 до 1, где 0 — ужасная модель, а 1 — идеальная модель. Как вы, вероятно, видите, 0.7 — довольно приличная модель, поэтому вы можете быть достаточно уверены в своих прогнозах погоды!

В начало

Множественный регрессионный анализ используется для проверки наличия статистически значимой связи между наборами переменных.Он используется для поиска тенденций в этих наборах данных.

Анализ множественной регрессии — это почти то же самое, что и простая линейная регрессия. Единственная разница между простой линейной регрессией и множественной регрессией заключается в количестве предикторов (переменных «x»), используемых в регрессии.

• Простой регрессионный анализ использует одну переменную x для каждой зависимой переменной «y». Например: (x ₁ , Y ₁ ).
• Множественная регрессия использует несколько переменных «x» для каждой независимой переменной: (x1) ₁ , (x2) ₁ , (x3) ₁ , Y ₁ ).

В линейной регрессии с одной переменной вы должны ввести одну зависимую переменную (например, «продажи») против независимой переменной (например, «прибыль»). Но вам может быть интересно, как различных типов продаж влияют на регрессию. Вы можете настроить свой X ₁ как один тип продаж, свой X ₂ как другой тип продаж и так далее.

Когда использовать множественный регрессионный анализ.

Обычной линейной регрессии обычно недостаточно, чтобы учесть все реальные факторы, влияющие на результат.Например, на следующем графике одна переменная (количество врачей) сопоставляется с другой переменной (ожидаемая продолжительность жизни женщин).

Изображение: Колумбийский университет

Из этого графика может показаться, что существует взаимосвязь между ожидаемой продолжительностью жизни женщин и количеством врачей в населении. На самом деле, это, вероятно, правда, и можно сказать, что это простое решение: увеличить количество врачей среди населения, чтобы увеличить продолжительность жизни. Но на самом деле вам придется учитывать другие факторы, например, вероятность того, что у врачей в сельской местности может быть меньше образования или опыта.Или, возможно, у них нет доступа к медицинским учреждениям, таким как травматологические центры.

Добавление этих дополнительных факторов заставит вас добавить дополнительные зависимые переменные в регрессионный анализ и создать модель множественного регрессионного анализа.

Вывод множественного регрессионного анализа.

Регрессионный анализ всегда выполняется в программном обеспечении, таком как Excel или SPSS. Выходные данные различаются в зависимости от того, сколько переменных у вас есть, но по сути это тот же тип выходных данных, который вы найдете в простой линейной регрессии.И еще кое-что:

.

• Простая регрессия: Y = b ₀ + b ₁ x.
• Множественная регрессия: Y = b ₀ + b ₁ x1 + b ₀ + b ₁ x2… b ₀ … b ₁ xn.

Выходные данные будут включать сводку, аналогичную сводке для простой линейной регрессии, которая включает:

Эти статистические данные помогут вам выяснить, насколько хорошо регрессионная модель соответствует данным. Таблица ANOVA в выходных данных даст вам p-значение и f-статистику.

Минимальный размер выборки

«Ответ на вопрос о размере выборки, по-видимому, частично зависит от целей
исследователя, исследуемых вопросов исследования и типа используемой модели
. Хотя есть несколько исследовательских статей и учебников, дающих
рекомендаций по минимальному размеру выборки для множественной регрессии, немногие согласны с
относительно того, насколько большой является достаточно большим, и не многие обращаются к прогнозирующей стороне MLR ». ~ Грегори Т.Кнофчинский

Если вы заинтересованы в нахождении точных значений квадрата коэффициента множественной корреляции, минимизации уменьшения
квадрата коэффициента множественной корреляции или имеете другую конкретную цель, статью Грегори Кнофчински стоит прочитать, и в ней есть множество ссылок для дальнейшего изучения. Тем не менее, многие люди просто хотят запустить MLS, чтобы получить общее представление о тенденциях, и им не нужны очень конкретные оценки. В таком случае вы можете использовать эмпирическое правило .В литературе широко говорится, что в вашей выборке должно быть более 100 наименований. Хотя иногда этого достаточно, вы будете в большей безопасности, если у вас будет не менее 200 наблюдений или еще лучше — более 400.

В начало

Переобучение может привести к плохой модели для ваших данных.

Переобучение — это когда ваша модель слишком сложна для ваших данных. — это происходит, когда размер вашей выборки слишком мал. Если вы поместите достаточно переменных-предикторов в свою регрессионную модель, вы почти всегда получите модель, которая выглядит значимой.

Хотя переоборудованная модель может очень хорошо соответствовать особенностям ваших данных, она не подойдет для дополнительных тестовых выборок или всей генеральной совокупности. Модель
p-значений, R-Squared и коэффициентов регрессии может вводить в заблуждение. По сути, вы слишком многого требуете от небольшого набора данных.

Как избежать переобучения

При линейном моделировании (включая множественную регрессию) у вас должно быть не менее 10-15 наблюдений для каждого члена, который вы пытаетесь оценить. Если меньше этого значения, вы рискуете переоснастить вашу модель.
«Условия» включают:

Хотя это эмпирическое правило является общепринятым, Грин (1991) идет дальше и предлагает, чтобы минимальный размер выборки для любой регрессии должен составлять 50 с дополнительными 8 наблюдениями на член. Например, если у вас есть одна взаимодействующая переменная и три переменных-предиктора, вам понадобится около 45-60 элементов в вашей выборке, чтобы избежать переобучения, или 50 + 3 (8) = 74 элемента, согласно Грину.

Исключения

Из эмпирического правила «10-15» есть исключения. В их числе:

1. Если в ваших данных присутствует мультиколлинеарность или размер эффекта небольшой. В этом случае вам нужно будет включить больше терминов (хотя, к сожалению, нет практического правила, сколько терминов добавить!).
2. Если вы используете логистическую регрессию или модели выживания, возможно, вам удастся обойтись всего лишь с 10 наблюдениями на один предиктор, если у вас нет экстремальных вероятностей событий, небольших размеров эффекта или переменных-предикторов с усеченными диапазонами.(Педуцци и др.)

Как обнаружить и избежать переобучения

Самый простой способ избежать переобучения — увеличить размер выборки путем сбора большего количества данных. Если вы не можете этого сделать, второй вариант — уменьшить количество предикторов в вашей модели, комбинируя или исключая их. Факторный анализ — это один из методов, который вы можете использовать для определения связанных предикторов, которые могут быть кандидатами для объединения.

1. Перекрестная проверка

Используйте перекрестную проверку для обнаружения переобучения: это разбивает ваши данные, обобщает вашу модель и выбирает модель, которая работает лучше всего.Одна из форм перекрестной проверки — это предсказанных R-квадратов . Большинство хороших статистических программ будет включать эту статистику, которая рассчитывается по формуле:

• Удаление одного наблюдения из ваших данных,
• Оценка уравнения регрессии для каждой итерации,
• Использование уравнения регрессии для прогнозирования удаленного наблюдения.

Перекрестная проверка не является волшебным лекарством для небольших наборов данных, и иногда четкая модель не может быть идентифицирована даже при адекватном размере выборки.

2. Усадка и повторная выборка

Методы сжатия и повторной выборки (например, этот R-модуль) могут помочь вам определить, насколько хорошо ваша модель может соответствовать новому образцу.

3. Автоматизированные методы

Автоматическую пошаговую регрессию не следует использовать как решение для переобучения небольших наборов данных. По данным Бабяка (2004),

«Проблем с автоматическим отбором, проводимым таким типичным способом, настолько много, что было бы трудно каталогизировать их все [в журнальной статье].”

Бабяк также рекомендует избегать одномерного предварительного тестирования или скрининга («скрытый вариант автоматического выбора»), дихотомии непрерывных переменных , что может значительно увеличить количество ошибок типа I, или многократного тестирования смешивающих переменных (хотя это может быть нормально, если разумно использовать).

Список литературы

Книги:
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Линдстром, Д. (2010). Краткое изложение статистики Шаума, второе издание (Schaum’s Easy Outlines), 2-е издание.McGraw-Hill Education
Журнальные статьи:

1. Бабяк, М.А., (2004). «То, что вы видите, может быть не тем, что вы получаете: краткое, нетехническое введение в переоснащение в моделях регрессионного типа». Психосоматическая медицина. 2004 май-июнь; 66 (3): 411-21.
2. Грин С.Б., (1991) «Сколько испытуемых требуется для проведения регрессионного анализа?» Многомерное исследование поведения 26: 499–510.
3. Peduzzi P.N., et. al (1995). «Важность событий для каждой независимой переменной в многомерном анализе, II: точность и точность оценок регрессии.” Журнал клинической эпидемиологии 48: 1503–10.
4. Peduzzi P.N., et. al (1996). «Имитационное исследование количества событий на переменную в логистическом регрессионном анализе». Журнал клинической эпидемиологии 49: 1373–9.

В начало

Посетите наш канал YouTube, чтобы увидеть сотни видеороликов по элементарной статистике, включая регрессионный анализ с использованием различных инструментов, таких как Excel и TI-83.

1. Аддитивная модель и мультипликативная модель
2. Как построить диаграмму рассеяния.
3. Как рассчитать коэффициенты корреляции Пирсона.
4. Как вычислить значение теста линейной регрессии.
5. Тест Чоу для разделенных наборов данных
6. Выбор вперед
7. Что такое кригинг?
8. Как найти уравнение линейной регрессии.
9. Как найти точку пересечения наклона регрессии.
10. Как найти наклон линейной регрессии.
11. Как найти стандартную ошибку наклона регрессии.
12. Mallows ’Cp
13. Коэффициент достоверности: что это такое и как его найти.
14. Квадратичная регрессия.
15. Регрессия четвертого порядка
16. Пошаговая регрессия
17. Нестандартный коэффициент
18. Далее: : Слабые инструменты

Интересный факт: Знаете ли вы, что регрессия предназначена не только для создания линий тренда. Это также отличный способ найти n-й член квадратичной последовательности.

В начало

Определения

1. ANCOVA.
2. Допущения и условия регрессии.
3. Бета / Стандартизированные коэффициенты.
4. Что такое бета-вес?
5. Билинейная регрессия
6. Тест Бреуша-Пагана-Годфри
7. Расстояние повара.
8. Что такое ковариата?
9. Регрессия Кокса.
10. Detrend Data.
11. Экзогенность.
12. Алгоритм Гаусса-Ньютона.
13. Что такое общая линейная модель?
14. Что такое обобщенная линейная модель?
15. Что такое тест Хаусмана?
16. Что такое гомоскедастичность?
17. Влиятельные данные.
18. Что такое инструментальная переменная?
19. Отсутствие посадки
20. Регрессия Лассо.
21. Алгоритм Левенберга – Марквардта
22. Какая линия лучше всего подходит?
23. Что такое логистическая регрессия?
24. Что такое расстояние Махаланобиса?
25. Неправильная спецификация модели.
26. Полиномиальная логистическая регрессия.
27. Что такое нелинейная регрессия?
28. Упорядоченная логит / упорядоченная логистическая регрессия
29. Что такое регрессия методом наименьших квадратов?
30. Переоборудование.
31. Экономные модели.
32. Что такое коэффициент корреляции Пирсона?
33. Регрессия Пуассона.
34. Пробит Модель.
35. Что такое интервал прогнозирования?
36. Что такое регуляризация?
37. наименьших квадратов с правильным правилом.
38. Регуляризованная регрессия
39. Что такое относительный вес?
40. Что такое остаточные участки?
41. Обратная причинность.
42. Регрессия хребта
43. Среднеквадратичная ошибка.
44. Полупараметрические модели
45. Смещение одновременности.
46. Модель одновременных уравнений.
47. Что такое ложная корреляция?
48. Модель структурных уравнений
49. Что такое интервалы допуска?
50. Анализ тенденций
51. Параметр настройки
52. Что такое взвешенная регрессия наименьших квадратов?
53. Y Шляпа объяснила.

В начало

Посмотрите видео или прочтите следующие шаги:

Регрессия — это подгонка данных к линии (Minitab также может выполнять другие типы регрессии, например квадратичную регрессию).Когда вы обнаружите регрессию в Minitab, вы получите диаграмму разброса ваших данных вместе с линией наилучшего соответствия, плюс Minitab предоставит вам:

1. Стандартная ошибка (насколько точки данных отклоняются от среднего).
2. R в квадрате: значение от 0 до 1, которое показывает, насколько хорошо ваши точки данных соответствуют модели.
3. Скорректировано ² рандов (скорректировано ² рандов с учетом точек данных, которые не соответствуют модели).

Регрессия в Minitab занимает всего пару щелчков мышью на панели инструментов и доступна через меню Stat.

Пример вопроса : Найдите регрессию в Minitab для следующего набора точек данных, которые сравнивают калории, потребляемые в день, и вес:
Калорий, потребляемых ежедневно (вес в фунтах): 2800 (140), 2810 (143), 2805 (144) , 2705 (145), 3000 (155), 2500 (130), 2400 (121), 2100 (100), 2000 (99), 2350 (120), 2400 (121), 3000 (155).

Шаг 1: Введите данные в два столбца в Minitab .

Шаг 2: Щелкните «Статистика», затем щелкните «Регрессия», а затем щелкните «График с аппроксимацией».”

Регрессия в выборе Minitab.

Шаг 3: Щелкните имя переменной для зависимого значения в левом окне. В этом примере вопроса мы хотим знать, влияет ли калорий на вес , поэтому калории являются независимой переменной (Y), а вес — зависимой переменной (X). Щелкните «Калории», а затем «Выбрать».

Шаг 4: Повторите шаг 3 для зависимой переменной X , веса.

Выбор переменных для регрессии Minitab.

Шаг 5: Нажмите «ОК». Minitab создаст линейный график регрессии в отдельном окне.

Шаг 4: Прочтите результаты. Помимо создания графика регрессии, Minitab предоставит вам значения для S, R-sq и R-sq (adj) в правом верхнем углу окна подобранного линейного графика.
с = стандартная ошибка.
R-Sq = Коэффициент детерминации
R-Sq (adj) = Скорректированный коэффициент детерминации (Скорректированный R в квадрате).

Вот и все!

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Линейная регрессия: простые шаги, видео. Найти уравнение, коэффициент, наклон

В комплекте:

Что такое простая линейная регрессия?

Как найти уравнение линейной регрессии:

1. Как найти уравнение линейной регрессии вручную .
2. Найдите уравнение линейной регрессии в Excel .
3. TI83 Линейная регрессия.
4. TI 89 Линейная регрессия

Поиск сопутствующих товаров:

1. Как найти коэффициент регрессии.
2. Найдите наклон линейной регрессии.
3. Найдите значение теста линейной регрессии.

Кредитное плечо:

1. Кредитное плечо в линейной регрессии.

Вернуться к началу

Если вы только начинаете знакомиться с регрессионным анализом, простой линейный метод — это первый тип регрессии, с которым вы столкнетесь в классе статистики.

Линейная регрессия — наиболее широко используемый статистический метод ; это способ смоделировать отношения между двумя наборами переменных. В результате получается уравнение линейной регрессии, которое можно использовать для прогнозирования данных.

Большинство программных пакетов и калькуляторов могут рассчитывать линейную регрессию. Например:

Вы также можете найти линейную регрессию вручную.

Перед тем, как приступить к расчетам, вы всегда должны строить диаграмму рассеяния, чтобы увидеть, подходят ли ваши данные примерно к линии. Почему? Потому что регрессия всегда дает вам уравнение, и это может не иметь никакого смысла, если ваши данные соответствуют экспоненциальной модели. Если вы знаете, что взаимосвязь нелинейна, но не знаете точно, что это за взаимосвязь, одним из решений является использование моделей линейных базисных функций, которые популярны в машинном обучении.

Этимология

«Линейный» означает линию. Слово Регрессия пришло от ученого XIX века сэра Фрэнсиса Гальтона, который ввел термин «регресс к посредственности» (на современном языке это регресс к среднему.Он использовал этот термин, чтобы описать феномен того, как природа имеет тенденцию ослаблять лишние физические черты из поколения в поколение (например, экстремальный рост).

Зачем нужны линейные отношения?

С линейными отношениями, т. Е. Линиями, работать легче, и большинство явлений естественно связаны линейно. Если переменные не связаны линейно , то математика может преобразовать эту связь в линейную, чтобы исследователю (то есть вам) было легче понять.

Что такое простая линейная регрессия?

Вы, вероятно, знакомы с построением линейных графиков с одной осью X и одной осью Y. Переменная X иногда называется независимой переменной, а переменная Y — зависимой переменной. Простая линейная регрессия отображает одну независимую переменную X против одной зависимой переменной Y. Технически в регрессионном анализе независимая переменная обычно называется переменной-предиктором, а зависимая переменная называется переменной критерия.Однако многие люди просто называют их независимыми и зависимыми переменными. Более продвинутые методы регрессии (например, множественная регрессия) используют несколько независимых переменных.

Регрессионный анализ может дать линейных или нелинейных графиков. Линейная регрессия — это когда отношения между вашими переменными можно описать прямой линией. Нелинейные регрессии образуют изогнутые линии. ( ^** )

Простая линейная регрессия для количества осадков за год.

Регрессионный анализ почти всегда выполняется компьютерной программой, поскольку выполнение уравнений вручную требует очень много времени.

** Поскольку это вводная статья, я сделал ее простой. Но на самом деле существует важное техническое различие между линейным и нелинейным, которое станет еще более важным, если вы продолжите изучать регрессию. Подробнее см. В статье о нелинейной регрессии.
К началу

Регрессионный анализ используется для поиска уравнений, соответствующих данным.Получив уравнение регрессии, мы можем использовать модель для прогнозов. Один из видов регрессионного анализа — это линейный анализ. Когда коэффициент корреляции показывает, что данные, вероятно, могут предсказать будущие результаты, а диаграмма разброса данных выглядит как прямая линия, вы можете использовать простую линейную регрессию, чтобы найти прогностическую функцию. Если вы помните из элементарной алгебры, уравнение прямой: y = mx + b . В этой статье показано, как получить данные, рассчитать линейную регрессию и найти уравнение y ’= a + bx . Примечание : если вы берете статистику AP, вы можете увидеть уравнение, записанное как b ₀ + b ₁ x, что одно и то же (вы просто используете переменные b ₀ + b ₁ вместо a + b.

Посмотрите видео или прочтите приведенные ниже инструкции, чтобы вручную найти уравнение линейной регрессии. Все еще не понимаете? Посмотрите репетиторов на Chegg.com. Ваши первые 30 минут бесплатно!

Уравнение линейной регрессии

Линейная регрессия — это способ моделирования взаимосвязи между двумя переменными.Вы также можете узнать это уравнение как формулу наклона . Уравнение имеет вид Y = a + bX, где Y — зависимая переменная (то есть переменная, которая идет по оси Y), X — независимая переменная (т.е. она нанесена на ось X), b — наклон линия и a — точка пересечения по оси y.

Первый шаг в поиске уравнения линейной регрессии — определить, существует ли связь между двумя переменными. Это часто является суждением исследователя. Вам также понадобится список ваших данных в формате x-y (т.е. два столбца данных — независимые и зависимые переменные).

Предупреждения:

1. Тот факт, что две переменные связаны, не означает, что одна вызывает другую. Например, несмотря на то, что существует связь между высокими баллами GRE и лучшей успеваемостью в аспирантуре, это не означает, что высокие баллы GRE обеспечивают хорошую успеваемость в аспирантуре .
2. Если вы попытаетесь найти уравнение линейной регрессии для набора данных (особенно с помощью автоматизированной программы, такой как Excel или TI-83), вы, , найдете его, , но это не обязательно означает, что уравнение является хорошим подходит для ваших данных.Один из методов состоит в том, чтобы сначала построить диаграмму рассеяния, чтобы увидеть, соответствуют ли данные примерно линии , прежде чем вы попытаетесь найти уравнение линейной регрессии.

Как найти уравнение линейной регрессии: шаги

Шаг 1: Составьте диаграмму своих данных, заполняя столбцы так же, как если бы вы заполняли диаграмму, если бы вы находили коэффициент корреляции Пирсона.

Тема	Возраст x	Уровень глюкозы у	xy	x 2	y 2
1	43	99	4257	1849	9801
2	21	65	1365	441	4225
3	25	79	1975	625	6241
4	42	75	3150	1764	5625
5	57	87	4959	3249	7569
6	59	81	4779	3481	6561
Σ	247	486	20485	11409	40022

Из приведенной выше таблицы Σx = 247, Σy = 486, Σxy = 20485, Σx2 = 11409, Σy2 = 40022.n — размер выборки (в нашем случае 6).

Шаг 2: Используйте следующие уравнения, чтобы найти a и b.

a = 65,1416
b = ,385225

Щелкните здесь, чтобы получить простые пошаговые инструкции по решению этой формулы.

Найдите :

• ((486 × 11 409) — ((247 × 20 485)) / 6 (11 409) — 247 ² )
• 484979/7445
• = 65,14

Найти b :

• (6 (20,485) — (247 × 486)) / (6 (11409) — 247 ² )
• (122 910 — 120 042) / 68 454 — 247 ²
• 2 868/7 445
• = .385225

Шаг 3: Вставьте значения в уравнение .
y ’= a + bx
y’ = 65,14 + 0,385225x

Вот как найти уравнение линейной регрессии вручную!

Понравилось объяснение? Ознакомьтесь со Справочником по статистике практического мошенничества, в котором есть еще сотни пошаговых решений, подобных этому!

* Обратите внимание, , что этот пример имеет низкий коэффициент корреляции и поэтому не годится для предсказания чего-либо.
К началу

Посмотрите видео или прочтите следующие шаги:

Уравнение линейной регрессии Microsoft Excel: шаги

Шаг 1: Установите Data Analysis Toolpak , если он еще не установлен. Для получения инструкций по загрузке пакета инструментов анализа данных щелкните здесь.

Шаг 2: Введите данные в два столбца в Excel. Например, введите данные «x» в столбец A и данные «y» в столбец b. Не оставляйте пустых ячеек между вашими записями.

Шаг 3: Щелкните вкладку «Анализ данных» на панели инструментов Excel.

Шаг 4: Нажмите «регрессия» во всплывающем окне, а затем нажмите «ОК».

Всплывающее окно «Анализ данных» имеет множество параметров, включая линейную регрессию.

Шаг 5: Выберите входной диапазон Y. Вы можете сделать это двумя способами: либо выбрать данные на листе, либо ввести местоположение ваших данных в поле «Введите диапазон Y». Например, если ваши данные Y находятся в диапазоне от A2 до A10, введите «A2: A10» в поле «Диапазон ввода Y».

Шаг 6: Выберите входной диапазон X , выбрав данные на рабочем листе или введя расположение данных в поле «Входной диапазон X».

Шаг 7: Выберите место, куда вы хотите поместить выходной диапазон , выбрав пустую область на листе или введя местоположение, куда вы хотите поместить ваши данные в поле «Диапазон вывода».

Шаг 8: Нажмите «ОК». Excel рассчитает линейную регрессию и заполнит ваш рабочий лист результатами.

Совет: информация об уравнении линейной регрессии дается в последнем выходном наборе (столбец коэффициентов). Первая запись в строке «Перехват» — «a» (точка пересечения по оси Y), а первая запись в столбце «X» — «b» (наклон).

К началу

Посмотрите видео или прочтите следующие шаги:

Две линии линейной регрессии.

TI 83 Линейная регрессия: обзор

Линейная регрессия утомительна и подвержена ошибкам, когда выполняется вручную, но вы можете выполнить линейную регрессию за время, необходимое для ввода нескольких переменных в список. Линейная регрессия даст разумный результат только в том случае, если ваши данные выглядят как линия на диаграмме рассеяния, поэтому, прежде чем вы найдете уравнение для линии линейной регрессии , вы можете сначала просмотреть данные на диаграмме рассеяния. См. Эту статью, чтобы узнать, как построить диаграмму рассеяния на TI 83.

TI 83 Линейная регрессия: шаги

Пример задачи: Найдите уравнение линейной регрессии (вида y = ax + b) для значений x 1, 2, 3, 4, 5 и значений y 3, 9, 27, 64 и 102.

Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы открыть экран списков. Если у вас уже есть данные в L1 или L2, очистите данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. Повторите для L2.

Шаг 2: Введите переменные x по очереди. Следуйте за каждым числом, нажимая клавишу ENTER. Для нашего списка вы должны ввести:
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER

Шаг 3: Используйте клавиши со стрелками для перехода к следующему столбцу L2.

Шаг 4: Введите переменные y по очереди. Следуйте за каждым числом, нажимая клавишу ввода. Для нашего списка вы должны ввести:
3 ENTER
9 ENTER
27 ENTER
64 ENTER
102 ENTER

Шаг 5: Нажмите кнопку STAT, затем с помощью клавиши прокрутки выделите «CALC».

Шаг 6: Нажмите 4, чтобы выбрать «LinReg (ax + b)». Нажмите ENTER, а затем снова ENTER. TI 83 вернет переменные, необходимые для уравнения. Просто вставьте указанные переменные (a, b) в уравнение линейной регрессии (y = ax + b).Для приведенных выше данных это y = 25,3x — 34,9 .

Вот как выполнить линейную регрессию TI 83!

К началу

Помните из алгебры, что наклон — это «m» в формуле y = mx + b .
В формуле линейной регрессии наклон равен a в уравнении y ’= b + ax .
Это в основном одно и то же. Итак, если вас попросят найти наклон линейной регрессии, все, что вам нужно сделать, это найти b таким же образом, как и m .
Вычислить линейную регрессию вручную, мягко говоря, непросто. Есть лот суммирования (это символ Σ, что означает сложение). Основные шаги приведены ниже, или вы можете посмотреть видео в начале этой статьи. В этом видео более подробно рассказывается о том, как проводить суммирование. Поиск уравнения также даст вам наклон. Если вы не хотите определять уклон вручную (или если вы хотите проверить свою работу), вы также можете использовать Excel.

Как найти наклон линейной регрессии: шаги

Шаг 1: Найдите следующие данные из предоставленной информации: Σx, Σy, Σxy, Σx ² , Σy ² .Если вы не помните, как получить эти переменные из данных, прочтите эту статью о том, как найти коэффициент корреляции Пирсона. Следуйте приведенным там шагам, чтобы создать таблицу и найти Σx, Σy, Σxy, Σx ² и Σy ² .

Шаг 2: Вставьте данные в формулу b (нет необходимости находить a ).

Если формулы пугают вас, вы можете найти более подробные инструкции о том, как работать с формулой, здесь: Как найти уравнение линейной регрессии: обзор.

Как найти наклон регрессии в Excel 2013

Подпишитесь на наш канал Youtube, чтобы получить больше советов и рекомендаций по статистике.

К началу

Коэффициент регрессии — это то же самое, что наклон линии уравнения регрессии . Уравнение для коэффициента регрессии, которое вы найдете в тесте AP Statistics: B ₁ = b ₁ = Σ [(x _i — x) (y _i — y)] / Σ [ (x _i — x) ² ].«Y» в этом уравнении — это среднее значение y, а «x» — среднее значение x.

Вы можете найти коэффициент регрессии вручную (как указано в разделе вверху этой страницы).
Однако вам не нужно рассчитывать коэффициент регрессии вручную в тесте AP — вы воспользуетесь калькулятором TI-83. Почему? Вычисление линейной регрессии вручную занимает очень много времени (дайте себе около 30 минут, чтобы выполнить вычисления и проверить их), а из-за огромного количества вычислений, которые вам нужно выполнить, , вы, скорее всего, сделаете математические ошибки.Когда вы найдете уравнение линейной регрессии на TI83, вы получите коэффициент регрессии как часть ответа.

Пример задачи : Найдите коэффициент регрессии для следующего набора данных:
x: 1, 2, 3, 4, 5.
y: 3, 9, 27, 64, 102.

Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы войти в СПИСКИ. Вам может потребоваться очистить данные, если у вас уже есть числа в L1 или L2. Чтобы очистить данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. При необходимости повторите для L2.

Шаг 2: Введите x-данные в список. Нажимайте клавишу ENTER после каждого ввода.
1 ВВОД
2 ВВОД
3 ВВОД
4 ВВОД
5 ВВОД

Шаг 3: Прокрутите до следующего столбца L2 с помощью клавиш со стрелками в правом верхнем углу клавиатуры.

Шаг 4: Введите y-данные:
3 ENTER
9 ENTER
27 ENTER
64 ENTER
102 ENTER

Шаг 5: Нажмите кнопку STAT, затем выделите «CALC.”Нажмите ENTER

Шаг 6: Нажмите 4, чтобы выбрать «LinReg (ax + b)». Нажмите Ввод. TI 83 вернет переменные, необходимые для уравнения линейной регрессии. Искомое значение> коэффициент регрессии> равно b, что составляет 25,3 для этого набора данных.

Вот и все!
Наверх

Две линии линейной регрессии.

Значения теста линейной регрессии используются в простой линейной регрессии точно так же, как значения теста (например, z-оценка или T-статистика) используются при проверке гипотез.Вместо работы с z-таблицей вы будете работать с таблицей t-распределения. Значение теста линейной регрессии сравнивается со статистикой теста, чтобы помочь вам поддержать или отклонить нулевую гипотезу.

Значение теста линейной регрессии: шаги

Пример вопроса : Для набора данных с размером выборки 8 и r = 0,454 найдите значение теста линейной регрессии.

Примечание : r — коэффициент корреляции.

Шаг 1: Найдите r, коэффициент корреляции, , если он еще не был указан вам в вопросе.В этом случае дается r (r = 0,0454). Не знаете, как найти r? См .: Коэффициент корреляции, чтобы узнать, как найти r.

Шаг 2: Используйте следующую формулу для вычисления тестового значения ( n — размер выборки):

Как решить формулу:

1. Замените переменные своими числами:
   T = .454√ ((8 — 2) / (1 — [. 454] ² ))
   • Вычтем 2 из n:
     8-2 = 6
   • Квадрат r:
     .454 × 0,454 = 0,206116
   • Вычесть шаг (3) из 1:
     1 — .206116 = .793884
   • Разделите шаг (2) на шаг (4):
     6 / .793884 = 7,557779
   • Извлеките квадратный корень из шага (5):
     √7,557779 = 2,74

     4

   • Умножьте r на шаг (6):
     .454 × 2,74

     4 = 1,24811026

Значение теста линейной регрессии, T = 1,24811026

Вот и все!

Нахождение тестовой статистики

Значение теста линейной регрессии бесполезно, если вам не с чем его сравнивать.Сравните свое значение со статистикой теста. Статистика теста также представляет собой t-показатель (t), определяемый следующим уравнением:
t = наклон линии регрессии выборки / стандартная ошибка наклона.
См .: Как найти наклон линейной регрессии / Как найти стандартную ошибку наклона (TI-83).

Вы можете найти рабочий пример расчета значения теста линейной регрессии (с альфа-уровнем) здесь: Коэффициенты корреляции.

К началу

Точки данных с кредитным плечом могут перемещать линию линейной регрессии.Они склонны быть выбросами. Выброс — это точка с очень высоким или очень низким значением.

Очки влияния

Если оценки параметров (стандартное отклонение выборки, дисперсия и т. Д.) Значительно изменяются при удалении выброса, эта точка данных называется влиятельным наблюдением .

Чем больше точка данных отличается от среднего других значений x, тем больше у нее рычага . Чем больше кредитное плечо у точки, тем выше вероятность того, что точка будет влиять на (т.е. это может изменить оценки параметров).

Кредитное плечо в линейной регрессии: как оно влияет на графики

В линейной регрессии влиятельная точка (выброс) будет пытаться подтянуть линию линейной регрессии к себе. На графике ниже показано, что происходит с линией линейной регрессии при включении выброса A:

Две линии линейной регрессии. Влиятельная точка A включена в верхнюю строку, но не в нижнюю.

Выбросы с крайними значениями X (значения, не попадающие в диапазон других точек данных) имеют больше возможностей для линейной регрессии, чем точки с менее экстремальными значениями x.Другими словами, крайних выбросов значения x переместят линию на больше, чем менее экстремальные значения.

На следующем графике показана точка данных за пределами диапазона других значений. Значения варьируются от 0 до примерно 70 000. Эта одна точка имеет значение x около 80 000, что выходит за пределы диапазона. Это влияет на линию регрессии намного больше, чем на точку на первом изображении выше, которая находилась внутри диапазона других значений.

Исключительно с высокой долей плеча. Точка сместила график еще больше, потому что она выходит за пределы диапазона других значений.

Как правило, выбросы со значениями, близкими к среднему значению x, будут иметь меньшее влияние, чем выбросы по отношению к краям диапазона. Выбросы со значениями x за пределами диапазона будут иметь больший рычаг. Значения, которые являются крайними по оси Y (по сравнению с другими значениями), будут иметь большее влияние, чем значения, близкие к другим значениям Y.

Нравится видео? Подпишитесь на наш канал Youtube.

Соединение с аффинным преобразованием

Линейная регрессия бесконечно связана с аффинным преобразованием.Формула y ′ = b + ax на самом деле не является линейной… это аффинная функция, которая определяется как линейная функция плюс преобразование. Так что это действительно следует называть аффинной регрессией, а не линейной!

Список литературы

Эдвардс, А. Л. Введение в линейную регрессию и корреляцию. Сан-Франциско, Калифорния: У. Х. Фриман, 1976.
Эдвардс, А. Л. Множественная регрессия и анализ дисперсии и ковариации. Сан-Франциско, Калифорния: У. Х. Фриман, 1979.

. ————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Коэффициент детерминации (R в квадрате): определение, расчет

Содержание :

Коэффициент детерминации (R в квадрате)

Коэффициент детерминации R ² используется для анализа того, как различия в одной переменной могут быть объяснены разницей во второй переменной.Например, , когда человек забеременеет, имеет прямое отношение к тому, когда он рожает.

Более конкретно, R-квадрат дает вам процентное изменение y, объясняемое переменными x. Диапазон составляет от 0 до 1 (т. Е. От 0% до 100% вариации y можно объяснить переменными x).

Коэффициент детерминации, R ² , аналогичен коэффициенту корреляции , R. Формула коэффициента корреляции покажет вам, насколько сильна линейная связь между двумя переменными.R в квадрате — это квадрат коэффициента корреляции, r (отсюда и термин r в квадрате). Посмотрите это видео, чтобы получить краткое определение r в квадрате и узнать, как его найти:

Нахождение R в квадрате / Коэффициент детерминации

Нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Шаг 1: Найдите коэффициент корреляции r (он может быть указан вам в вопросе). Пример, r = 0,543 .

Шаг 2: Возвести коэффициент корреляции в квадрат.
0,543 ² = ,295

Шаг 3: Преобразуйте коэффициент корреляции в проценты .
.295 = 29,5%

Вот и все!

Значение коэффициента детерминации

Коэффициент детерминации можно представить как процент. Это дает вам представление о том, сколько точек данных попадает в результаты линии, образованной уравнением регрессии.Чем выше коэффициент, тем больший процент точек проходит линия при построении точек данных и линии. Если коэффициент равен 0,80, то 80% точек должны попадать в линию регрессии. Значения 1 или 0 означают, что линия регрессии представляет все или никакие данные соответственно. Более высокий коэффициент является показателем лучшего соответствия наблюдениям.

CoD может быть отрицательным , хотя обычно это означает, что ваша модель плохо подходит для ваших данных.Он также может стать отрицательным, если вы не установили перехват.

Полезность R

²

Полезность R ² заключается в его способности находить вероятность будущих событий, попадающих в пределы прогнозируемых результатов. Идея состоит в том, что если добавить больше выборок, коэффициент будет показывать вероятность падения новой точки на линии.
Даже если существует сильная связь между двумя переменными, определение не доказывает причинно-следственную связь. Например, исследование дней рождения может показать, что большое количество дней рождения происходит в течение одного или двух месяцев.Это не означает, что беременность наступает по прошествии времени или смене времен года.

Синтаксис

Коэффициент детерминации обычно записывается как R ² _p. «P» указывает количество столбцов данных, что полезно при сравнении R ² различных наборов данных.

В начало

Что такое скорректированный коэффициент детерминации?

Скорректированный коэффициент детерминации (скорректированный R-квадрат) — это поправка для коэффициента детерминации, которая учитывает количество переменных в наборе данных. Он также наказывает вас за очки, не соответствующие модели.

Возможно, вы знаете, что небольшое количество значений в наборе данных (слишком маленький размер выборки) может привести к вводящей в заблуждение статистике, но вы можете не знать, что слишком много точек данных также может привести к проблемам. Каждый раз, когда вы добавляете точку данных в регрессионный анализ, ² рэндов будут увеличиваться. R ² никогда не уменьшается. Следовательно, чем больше очков вы добавите, тем лучше будет казаться, что регрессия «соответствует» вашим данным.Если ваши данные не совсем умещаются в строке, может возникнуть соблазн продолжить добавление данных, пока вы не найдете более подходящего.

Некоторые из добавленных вами баллов будут значительными (соответствовать модели), а другие — нет. R ² не заботится о мелочах. Чем больше вы добавите, тем выше коэффициент детерминации .

Скорректированный R ² можно использовать для включения более подходящего числа переменных, что избавит вас от соблазна продолжать добавлять переменные в ваш набор данных.Скорректированный R ² увеличится только в том случае, если новая точка данных улучшит регрессию больше, чем вы ожидаете случайно. R ² не включает все точки данных, всегда меньше, чем R ² и может быть отрицательным (хотя обычно положительным). Отрицательные значения вероятны, если R ² близок к нулю — после настройки значение немного опустится ниже нуля.

Подробнее см .: Скорректированный R-квадрат.

Посетите мой канал Youtube, чтобы получить больше советов по статистике и помощи!

Ссылки

Гоник, Л.(1993). Мультяшный справочник по статистике. HarperPerennial.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Точечная диаграмма

: определение, примеры, Excel / TI-83 / TI-89 / SPSS

Состав:

Что такое диаграмма рассеяния?

Диаграммы рассеяния

(также называемые графиками рассеяния ) аналогичны линейным графикам. На линейном графике используется линия на оси X-Y для построения непрерывной функции, а на точечной диаграмме — точек для представления отдельных фрагментов данных.В статистике эти графики полезны, чтобы увидеть, связаны ли две переменные друг с другом. Например, точечная диаграмма может предложить линейную зависимость (т. Е. Прямую линию).

Диаграмма рассеяния, предполагающая линейную зависимость.

Диаграммы рассеяния также называются графиками рассеяния, диаграммами рассеяния, диаграммами рассеяния и диаграммами рассеяния.

Корреляция в диаграммах рассеяния

Связь между переменными называется корреляцией. Корреляция — это просто еще одно слово, обозначающее «отношения».Например, ваш вес связан (коррелирован) с тем, сколько вы едите. Есть два типа корреляции: положительная корреляция и отрицательная корреляция. Если точки данных образуют линию от начала координат от низких значений x и y к высоким значениям x и y, то точки данных положительно коррелированы, , как на приведенном выше графике. Если график начинается с высоких значений y и продолжается до низких значений y, тогда график имеет отрицательную корреляцию .

Вы можете думать о положительной корреляции как о чем-то, что дает положительный результат.Например, чем больше вы тренируетесь, тем лучше ваше сердечно-сосудистое здоровье. «Положительный» не обязательно означает «хорошо»! Чем больше вы курите, тем выше вероятность рака, и чем больше вы водите машину, тем больше вероятность того, что вы попадете в автомобильную аварию.

В начало

Точечная диаграмма 3D

Трехмерный график рассеяния — это график рассеяния с тремя осями. Например, следующий трехмерный график разброса показывает оценки учащихся по трем предметам: чтение (ось y), письмо (ось x) и математика (ось z).

Учащийся A получил 100 баллов по письму и математике и 90 по чтению, а студент B получил 50 баллов по письму, 30 по чтению и 15 по математике.Для нескольких точек довольно легко построить трехмерные графики, но как только вы начнете разбираться в более крупных наборах данных, вам захочется использовать технологии. К сожалению, в Excel нет возможности создавать эти диаграммы. Статистические программы, обычно доступные в колледжах и университетах (например, SAS), могут их создавать. Доступно довольно много бесплатных вариантов, но я рекомендую:

• Plotly — это простой способ создать трехмерную диаграмму онлайн.
• Gnuplot: загружаемая программа. Легко использовать по сравнению с другими программами.
• R: Также можно скачать. Имеет довольно крутую кривую обучения, но справляется с большинством статистических вычислений. Если вам нужен общий пакет stst (в отличие от того, который просто создает диаграммы), это лучший вариант.

В начало

Что такое пузырьковая диаграмма?

Что такое пузырьковая диаграмма?

Пузырьковый график, показывающий суммы Medicare по услуге / специальности. Изображение: CMS.gov.

Пузырьковая диаграмма — это способ показать, как переменные связаны друг с другом.Она похожа на точечную диаграмму, только вместо точек здесь пузырьки разного размера.

Пузырьковые диаграммы — хороший выбор, если ваши данные имеют 3 серии / характеристики со связанным значением; Другими словами, вам нужно:

• категория со значениями для оси x,
• — категория со значениями для оси Y и
• категория со значениями для определения размеров ваших пузырей.

Они часто используются в финансовых целях и для использования с декартовыми самолетами.

Типы пузырьковой диаграммы

В его самой основной форме большие пузыри указывают на большие значения. Размещение пузыря по осям x и y дает вам информацию о том, что представляет собой пузырек. На этой диаграмме показана длина инвестиций (ось X), цена на момент покупки (ось Y) и относительный размер инвестиций на сегодняшний день.

Цветные пузырьковые диаграммы используют цвет для сортировки пузырьков по категориям. Например, я могу отсортировать свою инвестиционную диаграмму по акциям, облигациям и паевым инвестиционным фондам:

Картограмма — это пузырьковая диаграмма карты, на которой по осям x и y отложены долгота и широта.Размер пузыря может указывать на численность населения, количество нефтяных вышек, природные погодные явления или другие географические данные.

Графики иногда называют размерами:

• Двумерные диаграммы имеют только значения x и y. Они эквивалентны диаграмме рассеяния.
• Трехмерные диаграммы имеют оси x-y и размер пузырьков.
• Четырехмерные диаграммы имеют оси x-y, размер и цвет пузырьков.

В начало

Как построить диаграмму рассеяния: обзор

Простая диаграмма рассеяния.

Диаграмма рассеяния дает вам визуальное представление о том, что происходит с вашими данными. Точечные графики похожи на линейные графики. Единственное отличие состоит в том, что на линейном графике есть непрерывная линия, а на точечной диаграмме — ряд точек. Диаграммы разброса в статистике создают основу для простой линейной регрессии , где мы берем графики разброса и пытаемся создать пригодную для использования модель с помощью функций.Фактически, регрессия пытается провести черту через все эти точки.

В начало

Сделайте точечную диаграмму вручную

Посмотрите видео или прочтите ниже:

Чтобы вручную создать диаграмму рассеяния, нужно выполнить всего три шага.

Создайте точечную диаграмму: шаги

Пример вопроса: создать диаграмму рассеяния для следующих данных:

x	y
3	25
4.1	25
5	30
6	29
6,1	42
6,3	46

Шаг 1: Постройте график. Обозначьте оси x и y. Выберите диапазон, который включает максимумы и минимумы из заданных данных. Например, наши значения x изменяются от 3 до 6,3, поэтому диапазон от 3 до 7 будет подходящим.

Шаг 2: Нарисуйте первую точку на графике. Наша первая точка (3,25).

Шаг 3: . Нарисуйте оставшиеся точки на графике.

Вот и все!
В начало

Как построить диаграмму рассеяния в Excel

В этом разделе я расскажу, как создать диаграмму рассеяния в Excel, а также расскажу о некоторых дополнительных параметрах, таких как форматирование диаграммы, добавление меток и добавление линии тренда (уравнение линейной регрессии). Посмотрите видео или прочтите инструкции ниже:

Ступени

Шаг 1. Введите данные в два столбца (прокрутите вниз до второго примера, чтобы увидеть несколько снимков экрана).
Шаг 2: Нажмите «Вставить», затем нажмите «Разброс».
Шаг 3: Выберите тип участка. Например, щелкните первый значок (разброс только с маркерами).

Форматирование

Удалить легенду.

Шаг 1. Щелкните легенду правой кнопкой мыши и нажмите «Удалить».

Очистить белое пространство

Иногда ваши маркеры будут сгруппированы вверху или внизу справа на графике. Вот как избавиться от этого пробела, отформатировав горизонтальную и вертикальную оси.
Шаг 1. Щелкните вкладку «Макет», затем щелкните «Оси».
Шаг 2: Щелкните «Первичный горизонтальный», затем нажмите «Дополнительные основные горизонтальные параметры».
Шаг 3: Щелкните переключатель «Фиксированное значение», а затем введите значение, в котором должна начинаться горизонтальная ось. Нажмите «Закрыть».
Шаг 4: Повторите шаги с 1 по 3, выбрав «Вертикальный» вместо горизонтального.

Добавление меток диаграмм

Excel обычно добавляет ярлыки, которые вам не нужны, или пропускает ярлыки осей, которые вам нужны. Чтобы удалить ненужные ярлыки, вы можете щелкнуть и удалить.Вот как добавить ярлык:
Шаг 1. Перейдите на вкладку «Макет».
Шаг 2: Щелкните заголовки «Ось», а затем щелкните «Заголовок основной горизонтальной оси».
Шаг 3: Выберите позицию. например, вам может понадобиться заголовок под осью.
Шаг 4: Щелкните текст и введите новую этикетку.
Шаг 5: Повторите шаги с 1 по 4, выбрав «вертикальный» для вертикальной оси.

Совет : Если вам не нравится вертикальное расположение заголовка оси, щелкните правой кнопкой мыши и выберите «Формат заголовка оси.»Щелкните« Выравнивание », а затем выберите направление текста (например, горизонтальное).

Добавление линии тренда

Шаг 1: Щелкните вкладку «Макет».
Шаг 2: Щелкните «Линия тренда», а затем «Дополнительные параметры линии тренда».
Шаг 3: Щелкните «Показать уравнение в поле диаграммы», а затем нажмите «Закрыть».

Пример 2 : Создайте диаграмму разброса в Microsoft Excel, на которой будут нанесены следующие данные исследования зависимости между ростом и весом пациентов с преддиабетом:
Рост (дюймы): 72, 71,70,67,65,64 , 64,63,62,60
Вес (фунты): 180, 178,190,150,145,132,170,120,143,98

Шаг 1: Введите данные в электронную таблицу. Для правильной работы точечной диаграммы ваши данные должны быть введены в два столбца. В приведенном ниже примере показаны данные, введенные для роста (столбец A) и веса (столбец B).

Шаг 2: Выделите свои данные. Чтобы выделить данные, щелкните левой кнопкой мыши в верхнем левом углу данных и затем перетащите указатель мыши в нижний правый угол.

Шаг 3: Нажмите кнопку «Вставить» на ленте , затем нажмите «Разброс», затем нажмите «Разброс только с маркерами». Microsoft Excel создаст диаграмму рассеяния из ваших данных и отобразит диаграмму рядом с вашими данными в электронной таблице.

Совет: Если вы хотите изменить данные (и, следовательно, график), нет необходимости повторять всю процедуру. Когда вы вводите новые данные в любой из столбцов, Microsoft Excel автоматически вычисляет изменение и мгновенно отображает новый график.

В начало

Инструкции MATLAB

Используйте команду SCATTER (X, Y, S, C).

• Векторы X и Y должны быть одного размера.
• S — площадь каждого пузыря (в точках в квадрате).S может быть вектором или скаляром. Если скалярный, все маркеры будут одного размера.
• C — цвет производителя.

Точечная диаграмма в Minitab

Посмотрите видео о том, как создать диаграмму рассеяния в Minitab, или прочтите приведенные ниже инструкции.

Изображение: Penn State

Шаг 1: Введите данные в два столбца . Один столбец должен быть переменной x (независимая переменная), а второй столбец должен быть переменной y (зависимой переменной).Убедитесь, что вы поместили заголовок для ваших данных в первую строку каждого столбца — это упростит создание диаграммы рассеяния на шагах 4 и 5.

Шаг 2: Щелкните «График» на панели инструментов, а затем щелкните «График рассеяния».

Шаг 3: Щелкните «Простой» график рассеяния. В большинстве случаев это вариант, который вы будете использовать для диаграмм рассеяния в элементарной статистике. Вы можете выбрать один из других (например, диаграмму рассеяния с линиями), но вам редко понадобится их использовать.

Шаг 4: Щелкните имя вашей переменной y в левом окне, затем щелкните «Выбрать», чтобы переместить эту переменную y в поле переменной y.

Шаг 5: Щелкните имя своей переменной x в левом окне, затем щелкните «Выбрать», чтобы переместить эту переменную x в поле переменной x.

Шаг 6: Нажмите «ОК», чтобы создать диаграмму рассеяния в Minitab. График появится в отдельном окне.

Совет: Если вы хотите изменить отметки (интервал для оси x или оси y), дважды щелкните одно из чисел, чтобы открыть окно редактирования масштаба, где вы можете изменить различные параметры для вашего диаграмма рассеяния, включая отметки.
В начало

Как создать диаграмму рассеяния SPSS

В IBM SPSS Statistics есть несколько различных вариантов диаграмм разброса: Простая разброса, Матричная разброса, Простая точка, Наложение разброса и 3D-разброс. Какой тип диаграммы рассеяния вы выберете, в основном зависит от того, сколько переменных вы хотите построить:

• Простая диаграмма рассеяния отображает одну переменную относительно другой.
• Матричный точечный график отображает все возможные комбинации двух или более числовых переменных относительно друг друга
• Простой точечный график отображает одну категориальную переменную или одну непрерывную переменную.
• Наложенная диаграмма рассеяния отображает две или более пары переменных.
• 3D-диаграммы рассеяния — это трехмерные графики трех числовых переменных.

Посмотрите видео, чтобы узнать, как создать диаграмму рассеяния SPSS с помощью конструктора диаграмм, или прочтите ниже инструкции о том, как создать диаграмму с помощью диалогового меню прежних версий:

Как создать диаграмму рассеяния SPSS с помощью диалогового меню Legacy

Шаг 1: Щелкните «Графики», , затем наведите указатель мыши на «Устаревшие диалоги», затем щелкните «Точечная диаграмма / точка».

Шаг 2: Выберите тип точечной диаграммы. В этом примере щелкните «Простой разброс».
Шаг 3: Нажмите кнопку «Определить» , чтобы открыть окно «Простая диаграмма рассеяния».
Шаг 4: Щелкните переменную, которую вы хотите отобразить на оси Y , а затем щелкните стрелку слева от поля выбора «Ось Y».
Шаг 4: Щелкните переменную, которую вы хотите отобразить на оси X , а затем щелкните стрелку слева от поля выбора «Ось X».Нажмите «ОК», чтобы построить диаграмму рассеяния.

Вот и все!

Совет: Вам не нужно выбирать метки значений по, но если вы это сделаете, метки значений используются как метки точек для диаграммы разброса. Если вы не выберете переменную для маркировки наблюдений, выбросы и экстремумы могут быть помечены номерами наблюдений.
В начало

Точечная диаграмма на TI-89: обзор

Создание диаграммы рассеяния на TI-89 включает три этапа: доступ к редактору матрицы данных, ввод значений X и Y и последующее построение графика данных.

ТИ-89

Диаграмма рассеяния

на TI-89: Шаги:

Посмотрите видео или прочтите следующие шаги:

Пример задачи: построить диаграмму рассеяния для следующих данных: (1,6), (2,8), (3,9), (4,11) и (5,14).

Доступ к редактору матрицы данных
Шаг 1: Нажмите ПРИЛОЖЕНИЯ, затем перейдите к редактору «Данные / Матрица», нажмите ENTER и затем выберите «новый».

Шаг 2: Прокрутите вниз до «Переменная» и введите желаемое имя.Например, введите «scatterone». Примечание: вам не нужно нажимать клавишу АЛЬФА для доступа к альфа-клавиатуре. Просто введите!

Шаг 3: Нажмите ENTER ENTER.

Ввод значений X и Y
Шаг 1: Введите значения X в столбец «c1». Нажимайте ENTER после каждой записи.
Для нашего списка вам нужно будет нажать:
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER

Шаг 2: Введите значения Y под столбцом «c2» (используйте клавиши со стрелками для прокрутки к верхнему краю столбца).Нажимайте ENTER после каждой записи.
Для нашего списка вам нужно будет нажать:
6 ENTER
8 ENTER
9 ENTER
11 ENTER
14 ENTER

Графики данных
Шаг 1: Нажмите F2 для настройки графика.

Шаг 2: Нажмите F1.

Шаг 3: Выберите «разброс» рядом с «типом графика»

Шаг 4: Установите флажок рядом с «типом метки»

Шаг 5: Прокрутите до поля «x» и нажмите АЛЬФА) 1, чтобы ввести «c1».

Шаг 6: Прокрутите до поля «y» и нажмите ALPHA) 2, чтобы ввести «c2».

Шаг 7: Нажмите ENTER ENTER.

Шаг 8: Нажмите ромбовидную клавишу F3, чтобы просмотреть диаграмму рассеяния.

Шаг 9: Нажмите F2, а затем 9, чтобы график рассеяния отображался в правильном окне для данных.

Вот и все!

Посетите наш канал YouTube, чтобы получить больше советов и помощи!
В начало

TI 83 Точечная диаграмма

Посмотрите видео или прочтите следующие шаги:

TI 83 Точечная диаграмма: обзор

Создание диаграммы рассеяния на графическом калькуляторе TI-83 — это легкое дело с простым в использовании меню LIST.Чтобы построить график рассеяния TI 83 , вам понадобится набор двумерных данных. Двумерные данные — это данные, которые можно нанести на ось XY: вам понадобится список значений «x» (например, вес) и список значений «y» (например, высота). Значения XY могут быть в двух отдельных списках или они могут быть записаны как координаты XY (x, y). Как только они у вас появятся, это так же просто, как ввести списки в калькулятор и выбрать график.

TI 83 Точечная диаграмма: шаги

Пример задачи: Создайте диаграмму рассеяния TI 83 для следующих координат (2, 3), (4, 4), (6, 9), (8, 11) и (10, 12).

Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы открыть экран списков. Если у вас уже есть данные в L1 или L2, очистите данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. Повторите для L2.

Шаг 2: Введите переменные x по очереди. Следуйте за каждым числом, нажимая клавишу ENTER. Для нашего списка вы должны ввести:
2 ENTER
4 ENTER
6 ENTER
8 ENTER
10 ENTER

Шаг 3: Используйте клавиши со стрелками для перехода к следующему столбцу L2.

Шаг 4: Введите переменные y по очереди. Следуйте за каждым числом, нажимая клавишу ввода. Для нашего списка вы должны ввести:
3 ENTER
4 ENTER
9 ENTER
11 ENTER
12 ENTER
Шаг 5: Нажмите 2nd, затем нажмите STATPLOT (клавиша Y =).

Шаг 6: Нажмите ENTER, чтобы войти в StatPlots для Plot1.

Шаг 7: Нажмите ENTER, чтобы включить Plot1.

Шаг 8: Перейдите к следующей строке («Тип») и выделите диаграмму рассеяния (первое изображение).Нажмите Ввод.

Шаг 9: Стрелка вниз до «Xlist». Если «L1» не отображается, нажмите 2-ю и 1. Стрелку вниз до «Ylist». Если «L2» не отображается, нажмите 2-й и 2-й.

Шаг 10: Нажмите ZOOM, затем 9. На экране должна появиться диаграмма рассеяния.

Совет : Нажмите TRACE и нажимайте кнопки со стрелками вправо и влево, чтобы перемещаться от точки к точке, отображая значения XY для этих точек.

Вот как построить точечную диаграмму TI 83!

Потеряли путеводитель? Загрузите новый здесь с веб-сайта TI.

Посетите наш канал Youtube, чтобы получить дополнительную статистику, помощь и советы!

Список литературы

Бейер, В. Х. Стандартные математические таблицы CRC, 31-е изд. Бока Ратон, Флорида: CRC Press, стр. 536 и 571, 2002.
Агрести А. (1990) Анализ категориальных данных. Джон Вили и сыновья, Нью-Йорк.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Что такое линейная регрессия? — Статистические решения

Линейная регрессия — это основной и часто используемый тип прогнозного анализа.Общая идея регрессии состоит в том, чтобы исследовать две вещи: (1) хорошо ли помогает набор переменных-предикторов предсказывать переменную результата (зависимую)? (2) Какие переменные, в частности, являются значимыми предикторами переменной результата и каким образом они — на что указывает величина и знак бета-оценок — влияют на переменную результата? Эти оценки регрессии используются для объяснения взаимосвязи между одной зависимой переменной и одной или несколькими независимыми переменными. Простейшая форма уравнения регрессии с одной зависимой и одной независимой переменной определяется формулой y = c + b * x, где y = оценочная оценка зависимой переменной, c = постоянная, b = коэффициент регрессии и x = оценка по независимая переменная.

Именование переменных. Есть много имен зависимой переменной регрессии. Ее можно назвать выходной переменной, критериальной переменной, эндогенной переменной или регрессионным выражением. Независимые переменные можно назвать экзогенными переменными, переменными-предикторами или регрессорами.

Три основных применения регрессионного анализа: (1) определение силы предикторов, (2) прогнозирование эффекта и (3) прогнозирование тенденций.

Во-первых, регрессия может использоваться для определения силы воздействия, которое независимая (ые) переменная (ы) оказывает на зависимую переменную.Типичные вопросы: какова сила взаимосвязи между дозой и эффектом, расходами на продажи и маркетинг или возрастом и доходом.

Во-вторых, его можно использовать для прогнозирования эффектов или воздействия изменений. То есть регрессионный анализ помогает нам понять, насколько изменяется зависимая переменная при изменении одной или нескольких независимых переменных. Типичный вопрос: «Какой дополнительный доход от продаж я получу за каждую дополнительную 1000 долларов, потраченных на маркетинг?»

В-третьих, регрессионный анализ предсказывает тенденции и будущие значения.Для получения точечных оценок можно использовать регрессионный анализ. Типичный вопрос: «Какой будет цена на золото через 6 месяцев?»

11. Корреляция и регрессия

Слово корреляция используется в повседневной жизни для обозначения некоторой формы ассоциации. Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными. Мы также предполагаем, что связь является линейной, что одна переменная увеличивает или уменьшает фиксированную величину для увеличения или уменьшения единицы другой.Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для резюмирования ассоциации.

Коэффициент корреляции

Степень связи измеряется коэффициентом корреляции, обозначаемым r. Иногда его называют коэффициентом корреляции Пирсона по имени автора, и он является мерой линейной связи. Если для выражения взаимосвязи необходима изогнутая линия, необходимо использовать другие, более сложные меры корреляции.

Коэффициент корреляции измеряется по шкале от + 1 до 0 до — 1. Полная корреляция между двумя переменными выражается либо + 1, либо -1. Когда одна переменная увеличивается, а другая увеличивается, корреляция положительная; когда одно уменьшается, а другое увеличивается, оно отрицательно. Полное отсутствие корреляции обозначается цифрой 0. Рисунок 11.1 дает графическое представление корреляции.

Рисунок 11.1 Иллюстрированная корреляция.

Просмотр данных: диаграммы рассеяния

Когда исследователь собрал две серии наблюдений и хочет увидеть, существует ли между ними связь, он или она должны сначала построить диаграмму рассеяния.Вертикальная шкала представляет один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой — из временной шкалы или какой-либо наблюдаемой классификации, обычно результаты экспериментов наносят на вертикальную ось. Они представляют собой то, что называется «зависимой переменной». «Независимая переменная», такая как время или высота или какая-либо другая наблюдаемая классификация, измеряется по горизонтальной оси или базовой линии.

Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит.Эта путаница — триумф здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может или не может быть упомянута. Разумно, например, думать о росте детей как о зависимости от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смол и выходом никотина для определенных марок сигарет. «Высвобожденный никотин вряд ли имеет свое происхождение. в смоле: оба эти фактора изменяются параллельно с некоторыми другими факторами или факторами в составе сигарет.Урожайность одного не кажется «зависимым» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы разброса. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в базовую линию. В качестве еще одного примера, график ежемесячной смертности от сердечных заболеваний по сравнению с ежемесячными продажами мороженого покажет отрицательную связь.Однако вряд ли поедание мороженого защитит от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно температурой окружающей среды.

Расчет коэффициента корреляции

Педиатрический регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) 15 детей. Данные приведены в таблице 11.1 и диаграмме рассеяния, показанной на рисунке 11.2 Каждая точка представляет одного ребенка и помещается в точку, соответствующую измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Регистратор теперь проверяет узор, чтобы определить, кажется ли вероятным, что область, покрытая точками, находится в центре прямой линии или нужна изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общую тенденцию точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.

При построении диаграммы рассеяния (рисунок 11.2), чтобы показать рост и анатомические мертвые зоны легких у 15 детей, педиатр указал цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно расположить наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных четко идентифицируется как независимая. Соответствующие цифры для зависимой переменной затем могут быть исследованы в отношении возрастающего ряда для независимой переменной.Таким образом мы получаем ту же картину, но в числовой форме, как показано на диаграмме разброса.

Рис. 11.2 Диаграмма разброса зависимости между ростом и анатомическим мертвым пространством легких у 15 детей.

Расчет коэффициента корреляции осуществляется следующим образом: x представляет значения независимой переменной (в данном случае высота), а y представляет значения зависимой переменной (в данном случае анатомическое мертвое пространство). Используемая формула:

, которая может быть представлена ​​как:

Процедура калькулятора

Найдите среднее значение и стандартное отклонение x, как описано в разделе Найдите среднее и стандартное отклонение y:

Вычтите 1 из n и умножьте на SD (x) и SD (y), (n — 1) SD (x) SD (y)

Это дает нам знаменатель формулы.(Не забудьте выйти из режима «Stat».)

Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения и сохраните их.

110 x 44 = Min

116 x 31 = M +

и т. Д.

Сохраняется в памяти. Вычтите

MR — 15 x 144,6 x 66,93 (5426,6)

Наконец, разделите числитель на знаменатель.

r = 5426,6 / 6412,0609 = 0,846.

Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка.Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Причинная связь между двумя коррелированными переменными может быть, а может и не быть. Причем, если есть связь, она может быть косвенной.

Часть вариации одной из переменных (измеряемая по ее дисперсии) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть — как следствие неопределенных (часто «случайных») причин. Часть, обусловленная зависимостью одной переменной от другой, измеряется Ро.Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства объясняется ростом ребенка. Если мы хотим обозначить силу связи, для абсолютных значений r 0-0,19 считается очень слабым, 0,2-0,39 — слабым, 0,40-0,59 — умеренным, 0,6-0,79 — сильным и 0,8-1 — очень сильным. корреляция, но это довольно произвольные пределы, и следует учитывать контекст результатов.

Тест значимости

Чтобы проверить, очевидна ли связь и могла ли она возникнуть случайно, используйте тест t в следующем расчете:

вводится при n — 2 степенях свободы.

Например, коэффициент корреляции для этих данных составил 0,846.

Число пар наблюдений было 15. Применяя уравнение 11.1, мы имеем:

Вводя таблицу B при 15-2 = 13 степенях свободы, мы находим, что при t = 5,72, P <0,001, поэтому коэффициент корреляции можно рассматривать как очень значительный. Таким образом (как сразу видно из диаграммы рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла случайно.

Предположения, управляющие этим тестом:

1. Что обе переменные правдоподобно Нормально распределены.
2. Что между ними существует линейная зависимость.
3. Нулевая гипотеза состоит в том, что между ними нет связи.

Тест не следует использовать для сравнения двух методов измерения одной и той же величины, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом кажется распространенной ошибкой, поскольку значительный результат интерпретируется как означающий, что один метод эквивалентен другому.Причины широко обсуждались (2), но стоит вспомнить, что значительный результат мало что говорит нам о прочности отношений. Из формулы должно быть ясно, что даже при очень слабой связи (скажем, r = 0,1) мы получим значительный результат с достаточно большой выборкой (скажем, n больше 1000).

Ранговая корреляция Спирмена

График данных может выявить отдаленные точки далеко от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции.В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура по Спирмену заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.

Это приводит к простой формуле для ранговой корреляции Спирмена, Rho.

где d — разница в рангах двух переменных для данного человека. Таким образом, мы можем вывести таблицу 11.2 из данных в таблице 11.1.

Отсюда получаем, что

В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена можно проверить на значимость с помощью t-критерия, приведенного ранее.

Уравнение регрессии

Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда один изменяется на определенную величину, другой изменяется в среднем на определенную величину.Например, у детей, описанных ранее, больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x — независимую переменную, эта связь описывается как регрессия y по x.

Взаимосвязь может быть представлена ​​простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (термин — историческая аномалия) просто означает, что среднее значение y является «функцией» от x, то есть оно изменяется вместе с x.

Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, положительная или отрицательная корреляция. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо.Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если вообще пройдет. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две особенности линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние от базовой линии; второй — его наклон. Они выражаются в следующем уравнении регрессии :

С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной.Параметры α и β необходимо оценить по данным. Параметр обозначает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) обозначает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину y, изменяющуюся для увеличения x на единицу. Таким образом, он представляет степень уклона линии вверх или вниз.

и

можно показать, что

полезно, потому что мы вычислили все компоненты уравнения (11.2) при расчете коэффициента корреляции.

Расчет коэффициента корреляции по данным в таблице 11.2 дал следующее:

Применяя эти цифры к формулам для коэффициентов регрессии, мы имеем:

Следовательно, в этом случае уравнение регрессии y на x становится

Это означает, что в среднем на каждое увеличение высоты на 1 см увеличение анатомического мертвого пространства составляет 1,033 мл в диапазоне измерений .

Линия, представляющая уравнение, наложена на диаграмму разброса данных на рисунке 11.2. Чтобы нарисовать линию, нужно взять три значения x, одно в левой части диаграммы рассеяния, одно в середине и одно справа, и подставить их в уравнение следующим образом:

Если x = 110 , y = (1,033 x 110) — 82,4 = 31,2

Если x = 140, y = (1,033 x 140) — 82,4 = 62,2

Если x = 170, y = (1,033 x 170) — 82,4 = 93,2

Хотя двух точек достаточно, чтобы обозначить линию, три лучше для проверки.Поместив их на диаграмму разброса, мы просто проводим через них линию.

Рисунок 11.3 Линия регрессии, проведенная на диаграмме рассеяния, связывающая рост и анатомическое мертвое пространство легких у 15 детей

Стандартная ошибка наклона SE (b) определяется как:

, где — остаточное стандартное отклонение, определяемое как:

Это может будет показано, что алгебраически оно равно

Мы уже должны передать все члены в этом выражении. Таким образом получается квадратный корень из. Знаменатель (11.3) составляет 72,4680. Таким образом, SE (b) = 13,08445 / 72,4680 = 0,18055.

Мы можем проверить, существенно ли отличается наклон от нуля:

t = b / SE (b) = 1,033 / 0,18055 = 5,72.

Опять же, это n — 2 = 15 — 2 = 13 степеней свободы. Предположения, управляющие этим тестом:

1. Что ошибки предсказания приблизительно нормально распределены. Обратите внимание, это не означает, что переменные x или y должны быть нормально распределены.
2. Что отношения между двумя переменными линейны.
3. То, что разброс точек вокруг линии приблизительно постоянен — ​​мы не хотели бы, чтобы изменчивость зависимой переменной увеличивалась по мере увеличения независимой переменной. В этом случае попробуйте логарифмировать переменные x и y.

Обратите внимание, что критерий значимости для наклона дает точно такое же значение P, что и критерий значимости для коэффициента корреляции. Хотя эти два теста производятся по-разному, они алгебраически эквивалентны, что имеет интуитивный смысл.

Мы можем получить 95% доверительный интервал для b из

, где tstatistic from имеет 13 степеней свободы и равен 2,160.

Таким образом, 95% доверительный интервал составляет

от 1,033 — 2,160 x 0,18055 до 1,033 + 2,160 x 0,18055 = от 0,643 до 1,422.

Линии регрессии дают нам полезную информацию о данных, из которых они собраны. Они показывают, как одна переменная в среднем изменяется с другой, и их можно использовать, чтобы узнать, какой может быть одна переменная, если мы знаем другую — при условии, что мы зададим этот вопрос в рамках диаграммы разброса.Спроектировать линию на любом конце — экстраполировать — всегда рискованно, потому что отношения между x и y могут измениться или может существовать какая-то точка отсечения. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия, скажем, между возрастом от 5 до 10 лет, но спроецировать ее на возраст 30 лет. явно приведет к ошибке. Компьютерные пакеты часто производят перехват из уравнения регрессии без предупреждения, что это может быть совершенно бессмысленным.Рассмотрим регресс артериального давления по сравнению с возрастом у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что свидетельствует о повышении артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных мальчиков мужского пола!

Более сложные методы

Возможно использование нескольких независимых переменных — в этом случае метод известен как множественная регрессия. (3,4) Это наиболее универсальный из статистических методов, который может использоваться во многих ситуациях.Примеры включают: чтобы учесть более одного предиктора, возраст, а также рост в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимой переменной может быть результат после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но может повлиять на результат.

Общие вопросы

Если две переменные взаимосвязаны, связаны ли они причинно?

Часто путают корреляцию и причинно-следственную связь.Все, что показывает корреляция, — это то, что две переменные связаны. Может быть третья переменная, смешивающая переменная, связанная с ними обоими. Например, ежемесячные смерти от утопления и ежемесячные продажи мороженого положительно коррелируют, но никто не скажет, что эта связь была причинной!

Как проверить предположения, лежащие в основе линейной регрессии?

Ссылки

1. Russell MAH, Cole PY, Idle MS, Adams L.