Бифуркация – что это
Содержание статьи:
Что такое бифуркация простыми словами
Термин бифуркация произошел от латинского bifurcus(«раздвоенный»). В основе значения понятия лежат множественные преобразования или метаморфозы все возможных объектов по средству происходящего процесса изменения значимых параметров.
Для общего понимания понятия рассмотрим следующие примеры бифуркации:
- В биологии это симметричное деление бронхиального дерева, либо преобразование одного сосуда в два, равных по диаметру.
- В географии это расхождение русла реки на два разнонаправленных рукава.
- В научной фантастике в качестве примера можно привести параллельные разновременные отрезки, отвечающие за важные события, происходящие с персонажем.
- В образовании бифуркация понимается как разные учебно-методические направления одного класса.
- В жизни среднестатистического человека выступает в качестве кризисного момента, после которого полностью меняется образ жизни индивида.
Точка бифуркации
В широком смысле точка бифуркации интерпретируется как точка, в которой непосредственно происходит формализация объекта. Однако в каждой системе знаний это понятие трактуется индивидуально. Так, в синергетике и неравновесной динамике это смена существующего процесса работы на следующий по средству реализации показатель.
В свою очередь, в теории самоорганизации систем точка бифуркации понимается как начало кризиса. Здесь можно отметить режим неопределенности системы, когда финальный итог имеет два направления: переход на новый уровень, либо продолжение хаотичного движения системы в том же направлении. В теории хаоса выступает в качестве рычага, поворот которого приведет к фундаментальным изменениям.
Теория бифуркации
Данная теория универсальна, она применима ко всем системам (математическим, физическим и т.д.), где отмечены фазовые изменения последовательности, скачки реальной системы.
Можно выделить три основных типа фундаментальных изменений точки бифуркации:
- Перелом, изменение траектории движения.
- Выбор, т.е. смена параметра.
- Упорядоченность, по средству скачка происходит переход в новое состояние устойчивости.
Знание порядка изменения облегчает исследовательские мероприятия, помогает предугадать характер новых движений, при переходе в качественно другое состояние, основной системы и многое другое.
Точка бифуркации в истории
Поворотные пункты (точка бифуркации) являются ключевыми параметрами в развитии исторических событий, от конечного результата которых зависит ход всей истории. Наглядным примером считается выбор религии для Киевской Руси. Благодаря тесному отношению князя Владимира к православной культуре Византии, дальнейшее развитие всего государство пошло по выбранному им пути.
Можно отметить, что роль случайных событий
Точка бифуркации в психологии
В жизни каждого человека наступает некий переломный момент (точка бифуркации). В психологии явление получило терминологию, как правило, нужного момента. В данный период даже небольшое внешнее влияние может оказать колоссальное воздействие и привести к нужному результату. Прием получил широкое распространение в детской педагогике, а также актуален в психологии семейных отношений.
В эволюции
Процесс развития и усовершенствования живых организмов не стоит на месте. Постоянные изменения окружающей среды дают основания для образования новых видов особей. Можно сказать, что эволюция всего живого имеет тесную взаимосвязь с законами бифуркации. Вследствие смены одного постоянного состояния на вначале неустойчивое, а в конечном итоге получение окончательного результата по средству образования нового вида или нескольких подвидов, происходит процесс бифуркации для живых систем.
Бифуркация в экономике
Точка бифуркации в экономике — это отражение процесса развития экономических показателей в меньшую или большую сторону. Непосредственное влияние оказывают
Специалисты рассчитывают периодичность и прогнозируют дальнейшее развитие точки бифуркации, а также разрабатывают методы улучшения ситуации.
Точки бифуркации в кинематографе и литературе
Кино и искусство постоянно находятся в стадии прогресса. В современном творческом мире очень актуальна и интересна тематика параллельности пространства во времени. Большой популярностью пользуется кинематографическое произведение «Назад в будущее», именно здесь можно структурировано проследить за изменениями художественного времени. В обыденной жизни человек, принимая какое-либо решение, от которого
БИФУРКАЦИЯ — это… Что такое БИФУРКАЦИЯ?
бифуркация — и, ж. bifurcation f., лат. bifurcatio. 1. Раздвоение. Мак. 1908. Раздвоение реки, горного хребта, кровеносного сосуда и пр. Павленков 1911. Естествознание, ели оно не ограничивается бессмысленным набором фактов .. как это было у нас при… … Исторический словарь галлицизмов русского языка
бифуркация — раздвоение, (разветвление, разделение) на две части Словарь русских синонимов. бифуркация сущ., кол во синонимов: 3 • разветвление (14) • … Словарь синонимов
БИФУРКАЦИЯ — (от лат. bifurcus раздвоенный) в биологии раздвоение, вилообразное разделение, напр. трахеи на 2 главных бронха … Большой Энциклопедический словарь
БИФУРКАЦИЯ — в педагогике см. в ст. Фуркация … Большой Энциклопедический словарь
БИФУРКАЦИЯ — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Большой Энциклопедический словарь
БИФУРКАЦИЯ — БИФУРКАЦИЯ, бифуркации, жен. (от лат. bis дважды и furca вилы). Разделение, разветвление чего нибудь в двух направлениях (научн. книжн.). || разделение кровеносного сосуда или нерва (анат.). || Разветвление, разделение на специальные уклоны в… … Толковый словарь Ушакова
БИФУРКАЦИЯ — (новолат. bifurcatio раздвоение, разветвление, от лат. bis дважды, furca вилы), вилообразное раздвоение органа, напр. трахеи на два бронха, аорты на две общие подвздошные артерии, нервного или мышечного волокна. .(Источник: «Биологический… … Биологический энциклопедический словарь
БИФУРКАЦИЯ
БИФУРКАЦИЯ — (от лат. bifurcus раздвоенный) англ. bifurcation; нем. Bifurkation. Тип родственных отношений, связывающих семью супругов и их родителей, при к ром родственники по женской линии называются иначе, чем родственники по мужской линии. см. ФУРКАЦИЯ.… … Энциклопедия социологии
Бифуркация — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Политология. Словарь.
Что такое точка бифуркации? / Хабр
Другой кросс-пост с моего основного технического блога.Вообще-то, наверняка вы все это и так знаете, но чтобы не перегружать будущие статьи мне нужна просто ссылка на обьяснение. Так что попрошу пуристов не беспокоиться и дать мне обьяснить тем, кто этого еще не знает, может и не очень точно, но зато просто и «на пальцах», что такое точки бифуркации и с чем их едят.<o:p></o:p>
Начнем? Итак, все вы наверняка слышали проблему буриданова осла. Осел стоит возле двух совершенно одинаковых кучек сена на совершенно одинаковом расстоянии от осла справа и слева. Вопрос: как осел может выбрать одну из них? Ответ упомянутого Буридана был что осел помрет с голоду.<o:p></o:p>
Теперь давайте взглянем на эту картинку в воображении. Вот осел. Вот сено. Осел не в силах выбрать кучку и утомленный интеллектуальным усилием задремал. Одиночный фотон прорвался сквозь полуприкрытое ослиное веко и влетел с колбочку на сетчатке ослиного глаза, возбудив зрительный нерв. Нерв передал сигнал нейрону в ослином мозгу, и ослу приснился восхитительный (или ужасный, не имеет значения) сон, заставивший осла развернуться во сне. Когда осел проснулся, кучки уже оказались на разном расстоянии и вообще он видел перед мордой только одну, которую он и сьел. Вероятно, что потом он развернулся и сьел другую, но для нашего разговора это не имеет значения. А имеет значение то, что совершенно микроскопическое явление (в этом примере – на квантовом уровне, единичный фотон) в данной ситуации привело к изменению макромира – определило какая кучка сена сьедена первой.<o:p></o:p>
Вот это и есть точка бифуркации. Точка бифуркации это состояние системы, когда очень маленькое воздействие приводит к глобальным изменениям. В духе, «взмах крыла бабочки привел к урагану в Калифорнии». Кстати, «эффект бабочки» — это как раз о точках бифуркации.<o:p></o:p>
Осел между двумя равными кучками сена – это точка бифуркации. Витязь на распутье – это точка бифуркации. Ромул и Рем, всматривающиеся в небо в ожидании знака, на каком холме строить город – это точка бифуркации. Космический аппарат, летящий ровно в центре гравитации между Землей и Луной и не имеющий достаточно скорости, чтоб уйти от обеих, находится в точке бифуркации. Он станет или спутником Земли, или спутником Луны. Какой из них зависит от микроскопических воздействий вроде солнечного ветра или ударившего в спутник микрометеорита.<o:p></o:p>
Точки бифуркации есть не только в природе. Их полно, например, в экономике и политике. На фондовом или валютном рынке уровни поддержки или сопротивления являются точками бифуркации. Ценная бумага или валюта, достигшии их, сорвутся вниз или пойдут наверх в зависимости от очень незначительных факторов. Доверие потребителей очень часто проходит точки бифуркации, в которых одного хорошего или плохого известия достаточно, чтобы сохранить статус кво или привести к исходу к конкуренту в библейских пропорциях. Август 91-го был точкой бифуркации для СССР, в которую, надо признать, его постарались загнать в течении нескольких лет начиная с 1985-го. Выборы президента в США в 2000-м были точкой бифуркации. Не возьмись Верховный Суд голосовать за американцев, мы бы жили сейчас в сильно другом мире.<o:p></o:p>
Есть ситуации, когда точки бифуркации обильны и часты. Например, в потоках газов и жидкостей. Именно поэтому мы до сих пор не умеем предсказывать погоду. Скажем, шторм решительно надвигается на берег, а потом вдруг сворачивает на 90 градусов и уходит в океан, почему? Бабочка взмахнула крыльями в Шанхае… Кстати, валюты и ценные бумаги не зря имеют такое качество как «ликвидность», ситуация с точками бифуркации на биржах не так далека от ситуаций в аэрогидродинамике.<o:p></o:p>
Надеюсь, мне удалось обьяснить это понятие, поскольку мне придется ссылаться на него в грядущих статьях. На том пока и закончу.
Ну, и напоследок, обычная неформальная часть. Сегодня опять залез на тот любимый трейл и сделал фото городка Иссаквы поздней осенью:
А еще наконец собрался отсканировать салфетку с рисунком на темы карьеры в корпоративном мире, которую я нарисовал обьясняя предмет одному знакомому (вообще-то, предполагалось, что из арки справа вылезает изможденный человечек на всех четырех, который только что достиг блаженной цели — повышения по службе… и с изумлением смотрит на арку впереди него. Но времени в разговоре на это не хватило, пришлось просто сказать устно):
Значение слова «бифуркация» в 8 словарях
существительное
Значение слова бифуркация
Все словари Словарь Ушакова Политическая наука: Словарь-справочник Начала Современного Естествознания. Тезаурус Тезаурус русской деловой лексики Энциклопедический словарь Словарь Ефремовой Словарь медицинских терминов Большая Советская Энциклопедия
Словарь Ушакова
бифуркация
бифуркация, бифуркации, жен. (от лат. bis — дважды и furca — вилы). Разделение, разветвление чего-нибудь в двух направлениях (научн. книж.).
| разделение кровеносного сосуда или нерва (анат.).
| Разветвление, разделение на специальные уклоны в системе школьного преподавания (пед.).
| Разветвление реки на два разных русла, которые вливаются в разные бассейны.
Политическая наука: Словарь-справочник
бифуркация
приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание основных бифуркаций позволяет существенно облегчить исследование реальных систем (физических, химических, биологических. социальных и др.), в частности предсказать характер новых движений, возникающих в момент перехода системы в качественно другое состояние, оценить их устойчивость и область существования.
Начала Современного Естествознания. Тезаурус
бифуркация
(от лат. bifurcus — раздвоенный)
1) (в биологии) раздвоение, вилообразное разделение чего-либо на две ветви;
2) (в механике, динамике) разветвление в траектории движения системы в определенной точке либо приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркаций заложены в начале XX века французским математиком А. Пуанкаре и русским математиком А. М. Ляпуновым, позднее эта теория получила развитие в школе русского радиофизика А. А. Андронова. В настоящее время теория бифуркаций находит применение в физике, химии, биологии и др. науках, в основном, в междисциплинарных.
Тезаурус русской деловой лексики
бифуркация
Syn: раздвоение
Энциклопедический словарь
бифуркация
- приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание основных бифуркаций позволяет существенно облегчить исследование реальных систем (физических, химических, биологических и др.), в частности предсказать характер новых движений, возникающих в момент перехода системы в качественно другое состояние, оценить их устойчивость и область существования.
- в педагогике — см. в ст. Фуркация.
- (от лат. bifurcus — раздвоенный), в биологии- раздвоение, вилообразное разделение, напр. трахеи на 2 главных бронха.
Словарь Ефремовой
бифуркация
ж.
Раздвоение, разделение, разветвление реки, кровеносного сосуда и т.п. на два
потока.
Словарь медицинских терминов
бифуркация
разделение трубчатого органа на две ветви, приблизительно одинакового калибра, напр. Б. трахеи, Б. аорты.
Большая Советская Энциклопедия
бифуркация
(от лат. bifurcus ≈ раздвоенный) (мед.), разделение трубчатого органа (сосуда или бронха) на 2 ветви одинакового калибра, отходящие в стороны под одинаковыми углами.
Добавить свое значение
Значения слов синонимов к слову бифуркация
Синонимы к слову бифуркация
- двоение
- разветвление
- раздвоение
- разделение
БИФУРКАЦИЯ — это… Что такое БИФУРКАЦИЯ?
— термин, употребляемый в нек-рых разделах математики применительно к ситуации, когда нек-рый объект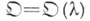 
зависит от параметра 
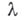(не обязательно скалярного) и в любой окрестности нек-рого значения 
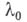последнего (бифуркационное значение, или точка Б.) исследуемые качественные свойства объекта 
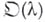не являются одинаковыми для всех 
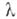. Соответствующие точные определения различны в различных случаях, но в общем они следуют (с теми или иными модификациями) двум вариантам:
а) Изучаемые качественные свойства объекта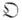 
состоят в существовании других объектов О, определенным образом связанных с ним. Б. состоит в том, что при изменении 
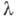объекты Овозникают или исчезают (в частности, они могут сливаться друг с другом, или из одного объекта может «рождаться» несколько). См. ниже — п. 1).
б) Сначала для объектов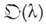 
определяется, когда два таких объекта считаются эквивалентными. (Определение должно быть таким, чтобы у эквивалентных объектов все интересующие нас качественные свойства были одинаковыми.) Изменение качественных свойств 
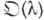в окрестности точки Б.
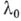, по определению, понимается в том смысле, что там имеются значения 
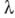с неэквивалентными 
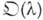. См. ниже — п. 2).
1) В теории операторов исходный объект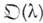 
— это нелинейный оператор 
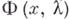в действительном банаховом пространстве, с действительным параметром 
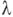, определенный в окрестности точки 
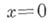и такой, что 
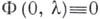. Ему при каждом фиксированном 
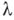сопоставляются другие объекты О — решения хнелинейного операторного уравнения 
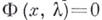. Точка В.- это точка, в к-рои происходит рождение нового, нетривиального решения этого уравнения. Именно, это такая точка 
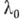, что для любого 
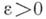существует 
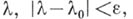при к-ром уравнение 
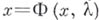имеет решение 
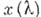, удовлетворяющее условиям 
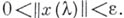Если 
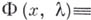
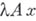, где A — линейный вполне непрерывный оператор, то понятие точки Б. совпадает с понятием характери-стич. значения оператора А.
Если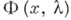 
— нелинейный вполне непрерывней оператор, непрерывно дифференцируемый в смысле Фреше и такой, что 
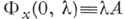, то точками Б. оператора Ф могут служить лишь характеристич. значения оператора А. Топологич. методом (см. [1], [2]) установлено, что каждое нечетнократное (в частности, простое) характеристич. значение оператора Аявляется точкой Б. оператора Ф. Аналогичное достаточное условие для случая четнократных характеристических значений формулируется с помощью понятия вращения векторного поля.
Если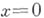 
— неизолированное решение уравнения 
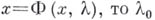есть точка Б. оператора Ф. Вариационным методом доказано (см. [1], [2]), что если 
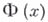— нелинейный вполне непрерывный оператор в гильбертовом пространстве, являющийся градиентом слабо непрерывного функционала, а 
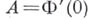— вполне непрерывный самосопряженный оператор, то каждое характеристич. значение оператора Аявляется точкой Б. оператора Ф. Понятие точки Б. видоизменяется также на случай больших решений 
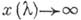при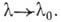 
Важное значение этих понятий и результатов состоит в том, что при сравнительно слабых ограничениях удается установить ветвление решения 
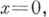в частности доказать неединственность решения нелинейной задачи. В ряде случаев более точную информацию дают аналитич. методы теории ветвления решений нелинейных уравнений (см. [5]).
2) В теории гладких динамич. систем рассматриваются однопараметрические (и отчасти двупараметрические [6]) семейства потоков (и каскадов; здесь рассматриваются лишь первые), причем выясняется, когда Б. «типичная», т. е. сохраняет свой характер при малом изменении рассматриваемого семейства [9]; употребительны оба варианта а) и б). При втором два потока считаются эквивалентными, если существует гомеоморфизм фазового пространства, переводящий траектории одного из них в траектории другого с сохранением направления движения. Имеется вполне удовлетворительная теория Б. однопараметрич. семейств потоков с двумерным фазовым многообразием [7], [9], а также локальный вариант, относящийся к окрестности положения равновесия или периодич. решения в гс-мерном случае [6].
В варианте а) изучаемые объекты О, к-рые сопоставляются данной дннамич. системе,- это положения равновесия и периодич. решения, а иногда также нек-рые инвариантные многообразия (преимущественно торы) и гиперболич. инвариантные множества. Рассматривается «рождение» этих объектов, происходящее как «локально», возле нек-рого положения равновесия или периодич. решения, так и «полулокально», в окрестности «замкнутого контура», образованного несколькими траекториями, к-рые при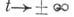 
стремятся к положению равновесия или к периодич. решениям. Возможен случай В., к-рая в определенном Смысле связана с подобным контуром, но к-рая происходит (с изменением параметра 
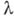) еще до его возникновения [8]. Часто рождение периодич. решений бывает удобно рассматривать, переписывая дифференциальное уравнение и условие периодичности в виде интегрального уравнения и применяя к нему соответствующие методы [5].
3) В теории особенностей отображений встречаются разнообразные Б. различных объектов (как исходных, так и сопоставленных им), в связи с чем имеются различные случаи использования этого термина (вернее, производных от него) (см. [10], [6], [11]), но еще чаще соответствующие понятия получают самостоятельные названия. Таковы, напр., версальные семейства (или деформации) (см. [6], [И], [12]), к-рые (в нек-ром смысле) описывают все возможные Б., могущие произойти при малой деформации рассматриваемого объекта, в частности сюда относятся семь элементарных катастроф [12], к-рые представляют собой «типичные» k-параметрические (
) семейства функций, включающие функцию с вырожденной критической точкой и определенные в окрестности последней; тем самым они описывают соответствующую Б. (Вообще, в иностранной литературе по теории особенностей вместо Б. часто говорят о «катастрофах».)
Лит.:[1] Красносельский М. А., Топологические методы в теории нелинейных интегральных уравнений, М., 1956; [2] Функциональный анализ, М., 1964; [3] Красносельский М. А., Положительные решения операторных уравнений, М., 1962; [4] Вайнберг М. М., Вариационные методы исследования нелинейных операторов, М., 1956; [5] Вайнберг М. М., Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [6] Арнольд В. И., «Успехи матем. наук*», 1972, т. 27, в. 5, 119-84; [7] Андронов А. А., Леонтович Е. А., Гордон И. И., Майер А. Г., Теория бифуркаций динамических систем на плоскости, М., 1967; [8] Гаврилов Н. К., Шильников Л. П., «Матем. сб.», 1972, т. 88, №4, 475-92; 1973, т. 90, №1,139-56; [9] Реiхоtо М. М., в кн.: Proceedings of the International Congress of Mathematics, Vancouver, 1974, v. 2, p. 315-19; [10] Том P.. «Успехи матам, наук». 1972., т,. 27. в 5, 51-7; [11] Арнольд В. И., «Успехи матем. наук», 1975, т. 30, в. 5, 3-65; [12] Brocker P., Lander L., Differentiable germs and catastrophes, Cambrige, 1975.
Д. В. Аносов, В. А. Треногий.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
БИФУРКАЦИЯ — это… Что такое БИФУРКАЦИЯ?
БИФУРКАЦИЯ — (лат. bifurcatio, от bis дважды, и firca вила). 1) раздвоение. Деление надвое. 2) разделение учебных занятий и самих учащихся на два различных курса. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИФУРКАЦИЯ [Словарь иностранных слов русского языка
бифуркация — и, ж. bifurcation f., лат. bifurcatio. 1. Раздвоение. Мак. 1908. Раздвоение реки, горного хребта, кровеносного сосуда и пр. Павленков 1911. Естествознание, ели оно не ограничивается бессмысленным набором фактов .. как это было у нас при… … Исторический словарь галлицизмов русского языка
бифуркация — раздвоение, (разветвление, разделение) на две части Словарь русских синонимов. бифуркация сущ., кол во синонимов: 3 • разветвление (14) • … Словарь синонимов
БИФУРКАЦИЯ — (от лат. bifurcus раздвоенный) в биологии раздвоение, вилообразное разделение, напр. трахеи на 2 главных бронха … Большой Энциклопедический словарь
БИФУРКАЦИЯ — в педагогике см. в ст. Фуркация … Большой Энциклопедический словарь
БИФУРКАЦИЯ — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Большой Энциклопедический словарь
БИФУРКАЦИЯ — БИФУРКАЦИЯ, бифуркации, жен. (от лат. bis дважды и furca вилы). Разделение, разветвление чего нибудь в двух направлениях (научн. книжн.). || разделение кровеносного сосуда или нерва (анат.). || Разветвление, разделение на специальные уклоны в… … Толковый словарь Ушакова
БИФУРКАЦИЯ — (новолат. bifurcatio раздвоение, разветвление, от лат. bis дважды, furca вилы), вилообразное раздвоение органа, напр. трахеи на два бронха, аорты на две общие подвздошные артерии, нервного или мышечного волокна. .(Источник: «Биологический… … Биологический энциклопедический словарь
БИФУРКАЦИЯ — [bifurcatio раздвоение, разделение на две ветви] разветвление на две части. В биологии син. термина дихотомия. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
Бифуркация — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Политология. Словарь.
БИФУРКАЦИЯ — это… Что такое БИФУРКАЦИЯ?
БИФУРКАЦИЯ — (лат. bifurcatio, от bis дважды, и firca вила). 1) раздвоение. Деление надвое. 2) разделение учебных занятий и самих учащихся на два различных курса. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИФУРКАЦИЯ [Словарь иностранных слов русского языка
бифуркация — и, ж. bifurcation f., лат. bifurcatio. 1. Раздвоение. Мак. 1908. Раздвоение реки, горного хребта, кровеносного сосуда и пр. Павленков 1911. Естествознание, ели оно не ограничивается бессмысленным набором фактов .. как это было у нас при… … Исторический словарь галлицизмов русского языка
бифуркация — раздвоение, (разветвление, разделение) на две части Словарь русских синонимов. бифуркация сущ., кол во синонимов: 3 • разветвление (14) • … Словарь синонимов
БИФУРКАЦИЯ — (от лат. bifurcus раздвоенный) в биологии раздвоение, вилообразное разделение, напр. трахеи на 2 главных бронха … Большой Энциклопедический словарь
БИФУРКАЦИЯ — в педагогике см. в ст. Фуркация … Большой Энциклопедический словарь
БИФУРКАЦИЯ — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Большой Энциклопедический словарь
БИФУРКАЦИЯ — БИФУРКАЦИЯ, бифуркации, жен. (от лат. bis дважды и furca вилы). Разделение, разветвление чего нибудь в двух направлениях (научн. книжн.). || разделение кровеносного сосуда или нерва (анат.). || Разветвление, разделение на специальные уклоны в… … Толковый словарь Ушакова
БИФУРКАЦИЯ — [bifurcatio раздвоение, разделение на две ветви] разветвление на две части. В биологии син. термина дихотомия. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
БИФУРКАЦИЯ — (от лат. bifurcus раздвоенный) англ. bifurcation; нем. Bifurkation. Тип родственных отношений, связывающих семью супругов и их родителей, при к ром родственники по женской линии называются иначе, чем родственники по мужской линии. см. ФУРКАЦИЯ.… … Энциклопедия социологии
Бифуркация — приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. 20 в., затем эта теория была развита А. А. Андроновым и учениками. Знание… … Политология. Словарь.
Эти примеры взяты из Кембриджского английского корпуса и из источников в Интернете. Любые мнения в примерах не соответствуют мнению редакторов Cambridge Dictionary или издательства Cambridge University Press или его лицензиаров.
Больше примеров Меньше примеров
О некоторых глобальных бифуркациях, связанных с исчезновением неподвижной точки седлового узла.Подготовка бифуркаций от периодических решений с пространственно-временной симметрией, включая модовые взаимодействия и резонансы. Дальнейшее увеличение амплитуды волны приводит к дальнейшим бифуркациям и, в конечном итоге, к хаотическому поверхностному возбуждению.Такие бифуркации могут показаться абсурдными, но замечательная коллекция наблюдений, касающихся людей, у которых полностью отделено мозолистое тело, показала обратное.Однако качественный анализ равновесий, бифуркаций или асимптотического поведения сложнее, чем с помощью моделей дифференциальных уравнений. Обсуждается зависимость стационарных мер от вспомогательного параметра, поэтому описываются бифуркации семейств случайных диффеоморфизмов.,Бифуркационный анализи его приложения
Линейная устойчивость динамических уравнений может быть проанализирована в двух частях: одна для скалярных уравнений, а другая для двумерных систем;
2.2.1. Анализ линейной устойчивости для скалярных уравнений
Для локального анализа ОДУ
x ‘= f (x)относительно точки равновесия x = x̣ мы разложим функцию f (x) в ряд Тейлора относительно точки равновесия x̣. Чтобы подчеркнуть, что мы проводим локальный анализ, обычно производят замену переменных из зависимой переменной x в локальную переменную.Теперь пусть
x (t) = x̣ + ϓ (t),, где предполагается, что ϓ (t) ≩1, так что мы можем оправдать отбрасывание всех членов порядка два и выше в разложении. Подставляя x (t) = x̣ + ϓ (t) в RHS от ODE, получаем;
f (x (t)) = f (x̣ + ϓ (t)) = f (x̣) + f ‘(x̣) ϓ (t) + f’ ‘(x̣) ϓ2 (t) 2 + … = 0 + f ‘(x̣) ϓ (t) + O (ϓ2),и отбрасывая члены более высокого порядка, получаем
f (x) ≇f’ (x̣) ϓ (t).Обратите внимание, что отбрасывание этих членов более высокого порядка действительно, так как ϓ (t) ≩1. Теперь подставляем x (t) = x̣ + ϓ (t) в LHS ОДУ,
ϓ ‘(t) = f’ (x̣) Ύ (т).Цель состоит в том, чтобы определить, есть ли у нас растущие или разлагающиеся решения. Если решения растут, то точка равновесия неустойчива. Если решение затухает, то неподвижная точка устойчива.
Чтобы определить, является ли решение стабильным или нестабильным, мы просто решаем ODE и получаем решение как
ϓ (t) = ϓ0exp (f ‘(x̣) t),, где ϓ0 — константа. Следовательно, решение растет, если f ‘(x̣)> 0, и затухает, если f’ (x̣) <0. В результате точка равновесия устойчива, если f '(x̣) <0, неустойчива, если f' (x̣)> 0 как указано в следующей теореме.
Теорема: Предположим, что для скалярного дифференциального уравнения
x ‘= f (x),производная функция f’ непрерывна на открытом интервале I, где точка равновесия x̣ϓI. Тогда точка равновесия x̣ локально устойчива, если f ‘(x̣) <0, и неустойчива, если f' (x̣)> 0.
Если точка равновесия стабильна и, кроме того,
limt → ∝x (t) = x̣,, то она называется асимптотически устойчивой точкой равновесия.
Пример: Определить устойчивость фиксированных точек для уравнения логистического роста
N ‘= fN = rN1-NK, гдеr> 0.Сначала мы найдем точки равновесия, установив
fṆ = 0, что дает точки w = 0, K.Далее мы вычисляем f ‘(N) и оцениваем его в точках равновесия.
f ‘(N) = r (1-2NK) при Ṇ = 0, f’ (0) = r> 0, soitisunstableatṆ = K, f ‘(K) = — r <0, soitislocallystable.2.2.2. Анализ линейной устойчивости для систем
Рассмотрим двумерную нелинейную систему
x ‘= f (x, y), y’ = g (x, y),и предположим, что (x̣, ỵ) является стационарным состоянием (точка равновесия) ), то есть
fx̣, ỵ = 0andg (x̣, ỵ) = 0.Теперь давайте рассмотрим небольшое возмущение из стационарного состояния (x̣, ỵ)
x = x̣ + u, y = ỵ + v,, где u и vare понимаются как малые как u≩1 и v≩1. Естественно спрашивать растут ли или исчезают или исчезают так, что x и yd будут удаляться от устойчивого состояния или двигаться к устойчивым состояниям. Если он удаляется, он называется точкой неустойчивого равновесия, если он движется к точке равновесия, то он называется точкой стабильного равновесия. Как и в скалярных уравнениях, путем расширения ряда Тейлора для f (x, y) и g (x, у);
u ‘= x’ = f (x, y) = f (x̣ + u, ỵ + v) = fx̣, ỵ + fxx̣, ỵu + fyx̣, ỵv + высшие условия… = fxx̣, ỵu + fyx̣, ỵv + высших порядков …Аналогично,
v ‘= y’ = g (x, y) = g (x̣ + u, ỵ + v) = gx̣, ỵ + gxx̣, +u + gyx̣, ỵv + высшие порядковые термины … = gxx̣, ỵu + gyx̣, ỵv + высшие порядковые термины ….Поскольку uand vare предполагается малым, члены более высокого порядка чрезвычайно малы, мы можем пренебречь членами более высокого порядка и получить следующая линейная система уравнений, управляющая эволюцией возмущений u и v,
u’v ‘= fx (x̣, ỵ) fy (x̣, ỵ) gx (x̣, ỵ) gy (x̣, ỵ) uv,где матрица fxfygxgy называется матрицей Якоби нелинейной системы.Вышеупомянутая линейная система для u и v имеет тривиальное стационарное состояние (u, v) = (0,0), и устойчивость этого тривиального устойчивого состояния определяется собственными значениями матрицы Якоби следующим образом:
Теорема: Точка равновесия (x̣, ỵ) дифференциального уравнения устойчива, если все собственные значения J, вычисленные в (x evaluated, ỵ) якобиана, имеют отрицательные вещественные части. Точка равновесия неустойчива, если хотя бы одно из собственных значений имеет положительную вещественную часть.
Как итог,
Асимптотически устойчивый : критическая точка асимптотически устойчива, если все собственные значения матрицы Якоби Jare отрицательны или имеют отрицательные вещественные части.
Нестабильный: Критическая точка нестабильна, если хотя бы одно собственное значение матрицы Якоби J положительно или имеет положительную вещественную часть.
Стабильно (или нейтрально устойчиво): Каждая траектория движется вокруг критической точки в пределах конечного диапазона расстояния.
Определение (гиперболическая точка): Равновесие называется гиперболическим, если все собственные значения матрицы Якоби имеют ненулевые вещественные части.
Гиперболические равновесия устойчивы (т.е.система структурно устойчива): небольшие возмущения порядка не изменяют качественно фазовый портрет вблизи равновесий. Более того, локальный фазовый портрет гиперболического равновесия нелинейной системы эквивалентен ее линеаризации. Это утверждение имеет математически точную форму, известную как Хартман-Гробман. Эта теорема гарантирует, что устойчивость стационарного состояния (x̣, ỵ) нелинейной системы совпадает со стабильностью тривиального устойчивого состояния (0,0) линеаризованной системы.
Определение (негиперболическая точка): Если хотя бы одно собственное значение матрицы Якоби равно нулю или имеет нулевую вещественную часть, то равновесие называется негиперболическим.
Негиперболические равновесия не являются устойчивыми (то есть система не является структурно устойчивой). Небольшие возмущения могут привести к локальному раздвоению негиперболического равновесия, то есть оно может изменить стабильность, исчезнуть или разбиться на множество равновесий. Некоторые называют такое равновесие именем бифуркации (см. Раздел ниже).
Пример: Рассмотрим следующую нелинейную автономную систему
x⋄ (t) = y (t) [x (t) -y (t)], E4
y⋄ (t) = x (t) [2 -y (т)].Равновесием являются точки (x̣, ỵ) = (0,0) и (x̣, ỵ) = (1,2), а матрица Якоби —
J = yx-12-y-x.Мы вычисляем якобиан в точке равновесия (0,0), где J (0,0) = 0-120, из которой следует, что собственные значения являются чисто мнимыми -ϙI) = 0.
Поскольку точка не гиперболическая, линеаризованная система не может сказать об устойчивости.Позже мы покажем, что это центр.
Для точки равновесия (1,2) якобиан J (1,2) = 200-1, следовательно, точка локально неустойчива (при
=1 = 1 и ϙ2 = -1,, где одно из собственных значений строго положительно). Поскольку это точка гиперболического равновесия, устойчивость неподвижной точки такая же, как в линеаризованной системе. Так что это тоже нестабильно.
Что такое «Симп» и почему он в тренде?
Simp. Вы, наверное, часто видели это слово в последнее время, но что оно значит и почему мы продолжаем его читать. Давайте углубимся.
Что такое Симп?
«Симп» — это сленговое выражение, используемое для насмешек над мужчинами, которые воспринимаются как чрезмерно вложенные и покорные женщинам. Как и большинство сленговых слов, у «простого» есть ряд определений. Некоторые считают, что это аббревиатура от «Sucker Idolizing Mediocre Pussy». Другие, такие как отмеченная наградами Академии рэп-группа Three 6 Mafia, которая помогла популяризировать эту фразу в 1999 году, используют ее в качестве антонима для «сутенера».«Они рэпят:« Я трель, работаю за рулем, сутенер, а не простак ». Он также использовался как портманто« сисси »и« сутенер ». Все они означают одно и то же.
В некоторых онлайн-сообществах «simp» существует в той же солнечной системе в сети, что и такие слова, как «cuck», «soyboy» или «beta» с некоторыми отличиями. В то время как «cuck» — уничижительное слово, используемое для выхолащивания, «simp» используется для вызова поведения, связанного с «белыми рыцарями» или «хорошими парнями». В этих случаях мужчины, которые просто считают, что им причитается секс за хорошее поведение.Тем не менее, хотя термин может использоваться для выделения этого поведения, он также используется для комедийного эффекта, поэтому было бы неслыханно видеть, как люди используют термин шутливо. В конце концов, ирония — это топливо, которое управляет интернетом.
Почему Simp Trending?
За последние несколько месяцев онлайн-валюта Simpsвзорвалась. Как и многие другие сленговые выражения, ориентированные на истощение мужчин, термин «простой» окружал сексистские круги в Reddit и 4chan. Согласно KYM, этот термин использовался более 10 000 раз в субреддите антифеминистская / r / MGTOW и более 12 000 раз в 4chan, из которых 1800 — из / pol /.
Фраза перешла к ироническому самоуничижительному употреблению в конце 2019 года с появлением «Simp Nation», мема TikTok, в котором человек, демонстрирующий «простое поведение», сразу же встречает фразу «добро пожаловать в Simp Nation». Подобно «Simp Nation», переназначение «Simp» сделало его предметом множества мемов, в которых обычно указывается и называется кто-то «Simp». Тем не менее, стоит признать, что этот термин ассоциировался с некоторыми из самых темных частей Интернета и может использоваться иронично или искренне.
В Твиттере многие отмечают, что «симп» использовался задолго до недавнего всплеска популярности, приписывая это изменение белым людям, внезапно «обнаружившим» сленговый термин. Наряду с этим массовым усыновлением пришла критика, что слово быстро теряет смысл и станет мертвым мемом быстрее, чем вы можете сказать «ОК, Бумер».
рис. Twitter.com/LylcjXxRhu
— шторм темной копы (@Chxndi) 3 марта 2020 г.
Белый человек никогда не должен был выучить слово симп https: // t.co / 6eHTcViPy7
— Кубок всасывания Гарфилд (@pink_garf) 27 февраля 2020 года
Термин «простой» встречался в течение десятилетий, и некоторые люди использовали его и злоупотребляли им в течение месяца, так что он потерял всякий смысл.
— Volt Vol10 дней до спасения (@VoltBD) 8 марта 2020 г.
Конечно, когда появляется мем, это как-то связано с выпуском видео PewdiePie. Немногие вещи так сильно влияют на продолжительность жизни мема, как один из его обзоров мемов, и разве вы не знаете, он выпустил один на Симпс только вчера.С более чем 4 миллионами просмотров менее чем за 24 часа, неудивительно, что мы видим внезапный простой всплеск.
Итак, вот оно. «Симп» — это мужчина, который демонстрирует явное, граничащее с патетическим, проявление привязанности к женщине в надежде получить романтическую любовь взамен, и это имеет тенденцию, потому что PewdiePie снял видео. Вы все можете вернуться к своему ежедневному упрощению.
,