Метод индукции: Индукция — Гуманитарный портал

Leave a reply

Индукция — Гуманитарный портал

Индукция — это познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение. В научном поиске (см. Методы научного познания) индукция предполагает движение познания от единичных утверждений об отдельных фактах к положениям, носящим более общий характер. В логике (см. Логика) термин «индукция» используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение» и понимается в более узком смысле: как умозаключение, в котором общий вывод строится на основе частных посылок. При этом посылки могут подтверждать или подразумевать истину, но не гарантируют её получения. Этим индукция принципиально отличается от дедукции (см. Дедукция), посредством которой из истинных посылок при соблюдении правил логического вывода всегда получаются истинные заключения.

Наиболее широко используемая разновидность индуктивных рассуждений — это перечислительные рассуждения, то есть рассуждения, содержащие переход от посылок, утверждающих, что все известные объекты из некоторой совокупности

A обладают свойством P, к заключению, утверждающему, что все — в том числе и неизвестные — объекты из A обладают P. Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P в будущем.

Индукция широко используется во всех областях научного познания, играя важную роль при построении эмпирических знаний и переходе от эмпирического знания к теоретическому. В науке основой индукции являются опыт, эксперимент и наблюдение, в ходе которых собираются отдельные факты. Затем, изучая эти факты, анализируя их, исследователь устанавливает общие и повторяющиеся признаки ряда явлений, входящих в определённый класс. На этой основе он строит индуктивное умозаключение, в качестве посылок которого выступают суждения о единичных объектах и явлениях с указанием их повторяющегося признака, и суждение о классе, включающем данные объекты и явления. В качестве вывода получают суждение, в котором признак, выявленный у совокупности единичных объектов, приписывается всему классу.
Ценность индуктивных выводов состоит в том, что они обеспечивают переход от единичных фактов к общим положениям, позволяют обнаруживать зависимости между явлениями, строить эмпирически обоснованные гипотезы и приходить к обобщениям.

В индуктивных рассуждениях различают полную и неполную индукцию:

  1. Полная индукция — это индукция, в которой делается заключение о том, что всем представителям класса изучаемых объектов принадлежит свойство P, на основании полученной при опытном исследовании информации о том, что
    каждому     представителю изучаемого класса принадлежит свойство P. Умозаключения полной индукции являются дедуктивными в том смысле, что заключение в них следует из посылок с логической необходимостью: при истинности посылок, применяя известные правила логики, мы не можем получить ложного заключения. Полная индукция применима в тех случаях, когда класс изучаемых объектов обозрим и все объекты этого класса могут быть перечислены. Таким образом, она подразумевает изучение каждого из объектов, входящих в класс, и нахождение на этой основе их общих характеристик. Однако в ряде случаев просто нет необходимости рассматривать абсолютно все предметы того или иного класса, в других случаях это невозможно сделать в силу необозримости класса изучаемых явлений или же в силу ограниченности человеческой практики. В таких ситуациях применяют неполную индукцию.
  2. Неполная индукция — это индукция, в которой делается заключение о том, что всем представителям класса изучаемых объектов принадлежит свойство P, на том основании, что некоторым представителям изучаемого класса принадлежит свойство P. Таким образом, она подразумевает изучение ограниченного числа объектов какого-либо определённого класса, поскольку, как правило, число всех случаев практически необозримо, а теоретическое доказательство для бесконечного числа этих случаев невозможно. Неполная индукция уже не является логически обоснованным рассуждением, так как с точки зрения логики справедливы только такие заключения, для получения которых не требуется никакой новой информации, кроме той, что содержится в посылках, но заключение неполной индукции говорит всегда больше, чем могут сказать её посылки.
    В этом, собственно, заключается познавательный смысл индукции — абстрагирующая работа мысли помогает получить новое знание при недостатке имеющихся [практических] знаний. Неполнота индукции может обусловливаться не только числом посылок (неполнота в отношении числа посылок), но и их характером (неполнота в отношении характера посылок).

    Существуют две разновидности неполной индукции: популярная индукция (или индукция через простое перечисление) и научная индукция:

    1. Популярная индукция строится как обобщение ряда наблюдений за сходными явлениями, в которых фиксируется какой-либо повторяющийся признак. Фиксация нового признака у ряда объектов происходит здесь, как правило, без предварительного плана исследований: обнаружив сходный признак у первых попавшихся предметов некоторого класса и не встретив ни одного противоречащего случая, переносят указанный признак на весь класс предметов. Отсутствие противоречащего случая является главным основанием для принятия индуктивного вывода.
      Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
    2. Научная индукция характеризуется поиском причинных зависимостей между явлениями и стремлением обнаружить существенные признаки объектов, объединяемых в класс. Выделяют три основных вида научной индукции:
      1. Индукция через отбор случаев. В отличие от популярной индукции, где учитывается лишь количество исследуемых случаев, индукция через отбор случаев принимает во внимание особенности каждой их группы.
      2. Индукция через исследование причинных связей.         Научная индукция широко используется и как метод нахождения причинных связей путём изучения некоторой совокупности обстоятельств, предшествующих наблюдаемому явлению. Варьируя обстоятельства и осуществляя каждый раз наблюдение за некоторым явлением, исследователь устанавливает его причину. Такой способ характеризует в частности многие виды экспериментального изучения объектов.
      3. Индукция через изучение единственного представителя некоторого класса. Научная индукция может строиться не только на основе изучения ряда явлений или объектов, входящих в некоторый класс, но и на основе изучения единственного представителя указанного класса. В этом случае при рассуждении о принадлежности или отсутствии определённого признака у объекта не должны использоваться такие его индивидуальные свойства, которые отличают его от других предметов того же класса.

Указанные разновидности неполной индукции играют исключительно важную роль в научном познании. Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода.

В этом процессе обоснование знаний, полученных путём индукции, обязательно предполагает движение от индуктивных обобщений к тому или иному частному случаю. Такого рода вывод представляет собой уже дедуктивное умозаключение. Тем самым индукция дополняется дедукцией, что и обеспечивает переход от вероятностного к достоверному знанию.

Поскольку индукция тесно связана с развитием опытного познания, она стала применяться уже в глубокой древности, хотя теоретически её простейшие формы начали анализироваться только в античной философии, в частности Сократом, который ввёл понятие индуктивных рассуждений, и Аристотелем, который рассматривал их как вспомогательные средства обоснования посылок силлогизмов (см. Силлогизм). У Аристотеля понимание индукции связывается с обобщением наблюдений и означает, по существу, способ умозаключения, посредством которого производится восхождение от частного к общему. Этот аристотелевский взгляд восприняли философы эпикурейской школы, защищавшие индукцию в споре со стоиками как единственный авторитетный метод доказательства законов природы.

Дальнейшее развитие теории индукции отмечается лишь в Новое время, когда активный рост науки, обусловленный накоплением, обобщением и систематизацией обширного эмпирического материала, поставил вопрос об исследовании способов научного открытия, а сами виды индуктивных рассуждений стали изучаться на предмет их надёжности. Важное значение в этом отношении имели сочинения Ф. Бэкона, который начал систематическое изучение индуктивных процедур, рассматривая их как единственно научный способ познания и противопоставив индукцию умозрительным рассуждениям. Поскольку методы аристотелевской силлогистики и индукция через простое перечисление подтверждающих случаев не могли быть использованы для анализа эмпирических обобщений, Бэкон в противовес «Органону» Аристотеля создаёт свой «Новый Органон» (1620), в котором излагает «каноны индукции» как методы открытия новых истин в науке. Позднее теория индукции развивалась в работах Дж. Ст. Милля, который предложил пять методов индуктивных рассуждений (каноны индукции Бэкона-Милля), посредством которых выводятся заключения о причинных связях между явлениями: метод сходства; метод различия; объединённый метод сходства и различия; метод остатков; метод сопутствующих изменений. Указанные индуктивные методы являются известными примерами правдоподобных рассуждений (см. Рассуждения правдоподобные). Впоследствии они получили ряд уточнений в работах других исследователей. Однако с помощью «канонов индукции» можно было сделать лишь относительно простые эмпирические обобщения и установить логические отношения между наблюдаемыми свойствами явлений. Когда наука стала исследовать более глубокие законы, раскрывающие сущность и внутренние механизмы явлений, стало очевидным, что эмпирические методы, опирающиеся на индукцию, не в состоянии этого сделать хотя бы потому, что здесь необходимо обращение к абстрактным, теоретическим понятиям. В связи с этим радикально изменился взгляд на индукцию, и вместо логики открытия она стала рассматриваться как метод проверки и обоснования гипотез. В рамках гипотетико-дедуктивного метода (см. Метод гипотетико-дедуктивный) именно эмпирически проверяемые следствия гипотезы могут быть проверены и подтверждены с помощью индуктивно установленных фактов. Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики. Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов.

С философской точки зрения наибольший интерес представляет проблема обоснования индукции — нахождения рационального базиса для признания легитимности индуктивных рассуждений. Важность проблемы обусловлена важностью индуктивных рассуждений для современной науки. Её успешное решение предполагает нахождение ответа на вопрос, на каком основании мы признаем некоторые из индуктивных рассуждений приемлемыми, несмотря на то, что во всяком индуктивном рассуждении истинность посылок не гарантирует истинности заключения. Все ответы, предложенные со времени поставившего этот вопрос Д. Юма, оказались безуспешными — всякая попытка обоснования индукции, предложенная до настоящего момента, в неявной форме предполагала легитимность индукции. В настоящее время определённой популярностью пользуется рассмотрение проблемы индукции, предложенное П. Стросоном, утверждающим, что проект обоснования индукции самопротиворечив. Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.

Урок 27. математическая индукция — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №27. Математическая индукция.

Глоссарий

Индукция; принцип математической индукции; полная индукция; неполная индукция.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Если рассмотреть значения квадратного трехчлена при равного они соответственно равны . Заметим, что эти числа являются простыми. Исходя из этого, можно сделать вывод, что при любом натуральном n число является простым. Но так ли это на самом деле?

Мы проверили справедливость утверждения при n от 1 до 14. Возьмем n равное 41 и подставим в наш квадратный трехчлен.

При n = 41, получаем

-составное число!

Получили составное число, т.е. противоречие нашему утверждению.

Для строгого доказательства утверждений на множестве натуральных чисел используют метод полной математической индукции. Продемонстрируем этот метод на примере:

Первым шагом проверим базу индукции, т.е. справедливость неравенства при наименьшем натуральном числе n=1

1 шаг: при n=1

–неравенство выполняется

Вторым шагом будет индуктивное предположение, т.е. предположим, что неравенство верно для некоторого натурального n.

2 шаг: предположим, что неравенство верно при некотором натуральном n.

неравенство выполняется.

Далее выполним индуктивный переход, т.е. докажем, что из предположения, сделанного на втором шаге следует справедливость аналогичного неравенства для следующего натурального числа n+1

следует

умножим обе части на положительное число 2

Получим верное неравенство

Но!

Т.к.

Из следует

Т.о. доказательство методом полной математической индукции состоит в:

1) Проверке справедливости утверждения при ;

2) Доказательстве, что если утверждение верно для натурального числа , то оно верно и для следующего за ним .

Пример:

Доказать, что для любого натурального значения n справедливо равенство

  1. При n=1 неравенство верно

  1. Предположим, что для некоторого натурального n неравенство верно.

Докажем, что если неравенство верно для некоторого n, то оно верно и для , т.е.

Прибавим к обеим частям верного по предположению равенства число :

Преобразуем правую часть равенства:

Таким образом из справедливости равенства

Следует справедливость равенства

Пример:

Докажите, что делится на 133 без остатка.

1 шаг: при

– произведение делится на 133 без остатка.

2 шаг: предположим, что сумма делится на 133 без остатка.

3 шаг:докажем, что делится на 133 без остатка.

В ходе преобразований получаем сумму, которая делится на 133 без остатка, т.к. первое ее слагаемое содержит множитель который делится на 133 без остатка по предположению индукции сделанного на 2 шаге, а во втором слагаемом одним из множителей является 133. Следовательно, и вся сумма делится на 133 без остатка.

Урок 39. метод математической индукции — Алгебра — 9 класс


Мы научились находить сумму большого количества чисел, кратных, например, числу 7.
Мы научились находить сумму большого количества слагаемых – степеней числа 2. А чему равна сумма квадратов первых трёхсот натуральных чисел?
За двести с лишним лет до нашей эры великий греческий учёный Архимед вывел формулу: сумма квадратов первых n натуральных чисел равна…
По этой формуле не составит большого труда найти сумму квадратов натуральных чисел от 1 до 300. Выполнив два умножения в столбик, получим 9 миллионов 45 тысяч пятьдесят.
Но как доказать, что эта формула верна для любого натурального числа n?
Проверим, верна ли формула при n равном единице. В левой части одно слагаемое, оно равно единице. В правой части в числителе дроби получаем 6, дробь равна 1.
При n равном единице формула верна.
Теперь предположим, что формула верна при n равном k, и докажем, что она верна при n равном k + 1.
Во-первых, упростим правую часть равенства.
В левой части воспользуемся предположением и заменим сумму первых k слагаемых дробью, потом приведём дроби к общему знаменателю и вынесем в числителе общий множитель k + 1 за скобки.
Выражение в скобках упростим и разложим на множители.
Мы привели обе части формулы для n равного k + 1 к одному и тому же виду, то есть утверждение для n равного k + 1 верно.
Итак, мы доказали, что если формула верна для какого-либо натурального числа k, то она верна и для следующего за ним натурального числа k + 1. Так как формула верна для n равного 1, то она верна и для n равного двум. А так как она верна для n равного двум, то она верна и для следующего натурального числа n равного трём, и так далее до бесконечности.
Применённый метод доказательства называется методом математической индукции.
Он основан на принципе математической индукции:
Утверждение верно при любом натуральном n, если выполняются два условия:
Первое. Утверждение верно при n = 1.
Второе. Из того, что утверждение верно для n = k следует, что оно верно для n = k + 1.
Докажем, что при любом натуральном n число 15n — 1 кратно 7, то есть делится на 7.
При n равном единице 15n — 1 равно 14. 14 кратно семи. При n равном единице утверждение верно.
Теперь предположим, что утверждение верно при n равном k, и докажем, что оно верно при n равном k + 1.
Выполним преобразования.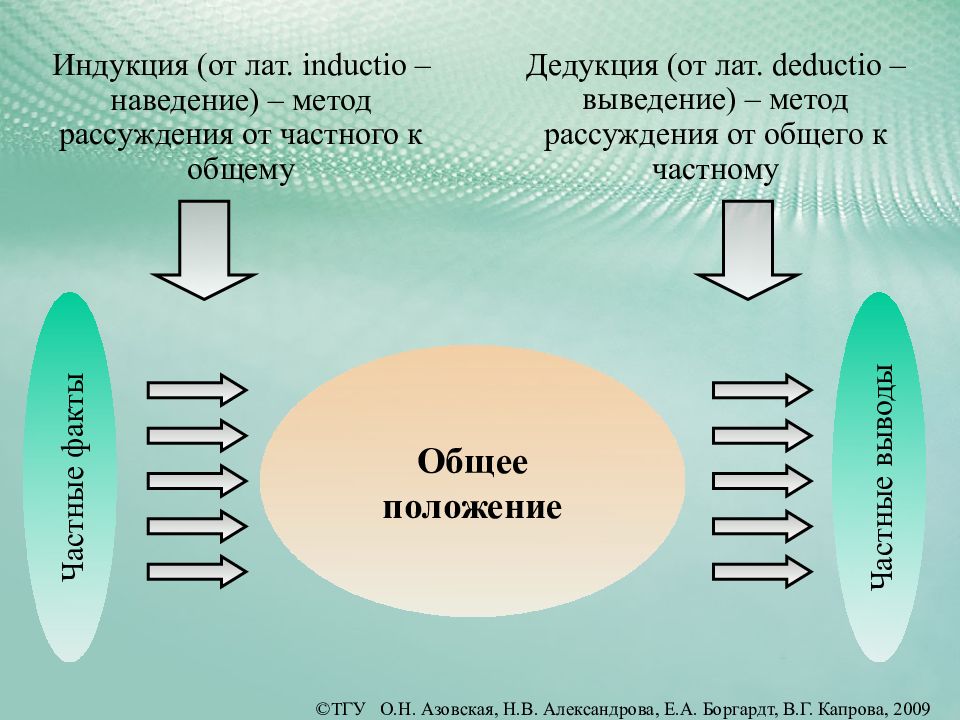 В первом слагаемом есть множитель 14, поэтому оно делится на 14. Второе слагаемое делится на 14 по предположению. Поэтому и вся сумма делится на 14, то есть утверждение при n равном k + 1 верно.
Тогда в силу принципа математической индукции утверждение 15n-1 кратно 7 верно при любом натуральном n.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Конечные числовые суммы

      Пусть   n   – произвольное натуральное число. Тогда справедливы следующие формулы, которые называют конечными числовыми суммами:

      Сумма бесконечно убывающей геометрической прогрессии является простейшим примером бесконечной числовой суммы (числового ряда). Ряды изучают в ВУЗовских курсах математики.

      Доказательство формул для конечных числовых сумм можно получить с помощью различных методов.

      К изложению одного из мощнейших методов доказательства этих, а также подобных формул, – методу (принципу) математической индукции мы сейчас и переходим.

Метод математической индукции

      Предположим, что нам требуется доказать, что некоторая формула верна при любом натуральном значении   n .   Предположим также, что мы:

  1. непосредственно проверили, что формула верна при   n = 1 ,
  2. доказали, что из справедливости формулы для некоторого номера   n ,   вытекает её справедливость для номера   n + 1 .

      Тогда в силу метода (принципа) математической индукции можно утверждать, что формула верна для всех натуральных чисел   n .

      Для примера дадим доказательство одной из формул, приведенных в предыдущем разделе.

      Пример 1. Доказать, что при всех натуральных   n   верна формула

(1)

      Решение. Для доказательства воспользуемся методом математической индукции:

  1. В случае   n = 1   формула (1) имеет вид

    и является верной.

  2. Докажем, что из справедливости равенства (1), вытекает справедливость равенства

    полученного из равенства (1) при помощи замены   n   на   n + 1 .

          Действительно,

          Следовательно, формула (2) верна, откуда из принципа математической индукции заключаем, что формула (1) верна для всех натуральных значений   n .

      Пример 2. Доказать, что число   n5 – n   делится на   5   при всех натуральных значениях n .

      Решение. Для доказательства снова воспользуемся методом математической индукции:

  1. В случае   n = 1   число   n5 – n   равно   0   и, конечно же, делится на   5 .

    Таким образом, при   n = 1   требуемое утверждение верно.

  2. Теперь докажем, что из того, что число   n5 – n   делится на   5   вытекает, что число

    (n + 1)5 – (n + 1)

    также делится на   5 .

          Действительно, пусть

    n5 – n = 5k ,

    где   .

          Тогда поскольку

    (n + 1)5 = n5 + 5n4 +
    + 10n3 + 10n2 + 5n + 1

    (см. Таблицу 1 из раздела справочника «Формулы сокращенного умножения: степень суммы и степень разности»), то

    (n + 1)5 – (n + 1) =
    = (n5 – n)+
    + 5n4 +
    + 10n3 + 10n2 + 5n =
    = 5k + 5n4 + 10n3 +
    + 10n2 + 5n =
    = 5 (k + n4 +
    + 2n3 + 2n2 + n) ,

    т. 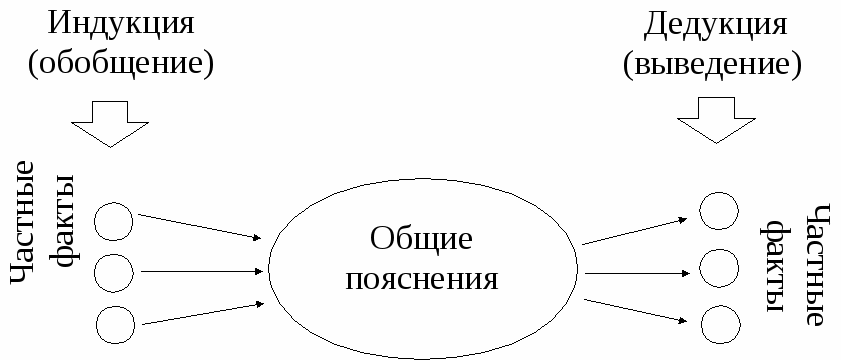е. делится на   5 .

          В соответствии с принципом математической индукции все доказано.

 

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Механические методы индукции родов | Cochrane

Индукция родов является обычной акушерской процедурой, которая проводится тогда, когда риск продолжения беременности перевешивает пользу.

Механические методы индукции были разработаны для стимулирования созревания шейки матки и начала родов путем растяжения шейки матки. Это один из самых старых методов стимуляции родов. В последнее время фармакологические простагландины (вагинальный и интрацервикальный простагландин Е2, вагинальный и пероральный мизопростол) и окситоцин частично заменили механические методы. Целью этого обзора 71 рандомизированного контролируемого испытания (9722 женщины) было определение влияния механических методов на созревание шейки матки или индукцию родов по сравнению с отсутствием лечения простагландинами и окситоцином у женщин в третьем триместре беременности.

Обзор включает в себя 71 рандомизированное контролируемое испытание (всего 9722 женщины), с диапазоном от 39 до 588 женщин в одном исследовании. В большинстве исследований сообщалось о кесаревом сечении; все другие результаты основаны на значительно меньшем числе женщин. Механические методы были столь же эффективны, как и простагландины, в достижении родоразрешения в течение 24 часов с начала процедуры, с меньшим числом случаев гиперстимуляции матки. Риск кесарева сечения не различался. В нескольких исследованиях рассматривался риск инфекции, который, как представляется, не был выше при использовании механических методов. Таким образом, можно считать, что механические методы имеют меньше побочных эффектов по сравнению с простагландинами. В одном исследовании, в котором сообщалось о материнском дискомфорте, было продемонстрировано больше дискомфорта во время созревания с простагландинами по сравнению с введением катетера Фолея и с двойными баллонными устройствами по сравнению с катетерами Фолея. Этот исход может повлиять на выбор метода и является важным вопросом для рассмотрения в будущих исследованиях. Механические методы были более эффективными, чем индукция окситоцином. Не сообщалось о серьезных побочных эффектах у новорожденных и матерей и они не отличались между вмешательствами.

ИНДУКЦИЯ • Большая российская энциклопедия

  • В книжной версии

    Том 11. Москва, 2008, стр. 356

  • Скопировать библиографическую ссылку:

Авторы: В. К. Финн

ИНДУ́КЦИЯ (лат. inductio – на­ве­де­ние), по­зна­ва­тель­ная про­це­ду­ра, по­сред­ст­вом ко­то­рой из срав­не­ния на­лич­ных фак­тов вы­во­дит­ся обоб­щаю­щее их ут­вер­жде­ние. В от­ли­чие от де­дук­ции, в ко­то­рой ис­тин­ность за­клю­че­ния не­об­хо­ди­мо сле­ду­ет из ис­тин­но­сти по­сы­лок, ин­дук­тив­ный вы­вод яв­ля­ет­ся лишь ве­ро­ят­но­ст­ным, или прав­до­по­доб­ным.

Ин­дук­тив­ные рас­су­ж­де­ния об­су­ж­да­лись Со­кра­том и Ари­сто­те­лем, ко­то­рый в «Ана­ли­ти­ках» рас­смат­ри­вал их как вспо­мо­га­тель­ные сред­ст­ва обос­но­ва­ния по­сы­лок сил­ло­гиз­мов.

Сис­те­ма­тич. изу­че­ние ин­дук­тив­ных про­це­дур на­чал Ф. Бэ­кон, пред­ло­жив­ший ме­тод ана­ли­за, от­бо­ра и обоб­ще­ния дан­ных опы­та, ве­ду­щий к по­зна­нию их при­чин (таб­ли­цы при­сут­ст­вия, от­сут­ст­вия и сте­пе­ней свойств изу­чае­мых яв­ле­ний). Он рас­смат­ри­вал И. как един­ст­вен­но на­уч. спо­соб по­зна­ния, про­ти­во­пос­тав­ляя её умо­зрит. рас­су­ж­де­ни­ям.

Опи­ра­ясь на идеи Бэ­ко­на, Дж.  С. Милль пред­ло­жил пять ме­то­дов ин­дук­тив­ных рас­су­ж­де­ний (ме­то­ды Мил­ля), по­сред­ст­вом ко­то­рых вы­во­дят­ся за­клю­че­ния о при­чин­ных свя­зях ме­ж­ду яв­ле­ния­ми (ме­то­ды сход­ст­ва, раз­ли­чия, объ­еди­нён­ный ме­тод сход­ст­ва и раз­ли­чия, ме­тод ос­тат­ков и ме­тод со­пут­ст­вую­щих из­ме­не­ний). Ин­дук­тив­ные ме­то­ды Мил­ля, яв­ляю­щие­ся при­ме­ра­ми прав­до­по­доб­ных рас­су­ж­де­ний, по­лу­чи­ли ряд уточ­не­ний сред­ст­ва­ми совр. ло­ги­ки (Г. Х. фон Вригт, В. К. Финн и др.).

При­зна­ние И. в ка­че­ст­ве ре­шаю­щей по­зна­ват. про­це­ду­ры ха­рак­те­ри­зу­ет тео­рию по­зна­ния эм­пи­риз­ма.

Скеп­тич. взгляд Д. Юма на И., cо­гласно ко­то­рому ин­дук­тив­ные обоб­ще­ния не мо­гут быть обос­но­ва­ны и яв­ля­ют­ся лишь ре­зуль­та­том ас­со­циа­ции идей, был раз­вит К. Поп­пе­ром, счи­тав­шим, что пра­ви­ла ин­дук­тив­но­го вы­во­да не мо­гут быть сфор­му­ли­ро­ва­ны, и от­ри­цав­шим по­зна­ват. зна­че­ние ин­дук­ции.

Тео­рии И. , ос­но­ван­ные на ве­ро­ят­но­ст­ном под­хо­де, бы­ли раз­ви­ты в ин­дук­тив­ной ло­ги­ке Х. Рей­хен­ба­ха и Р. Кар­на­па. В совр. ис­сле­до­ва­ни­ях по ис­кус­ст­вен­но­му ин­тел­лек­ту фор­ма­ли­за­ция И. осу­ще­ст­в­ля­ет­ся сред­ст­ва­ми ло­ги­ки, ал­го­рит­мич. язы­ков и баз дан­ных с не­пол­ной ин­фор­ма­ци­ей.

Индукция и дедукция. Какой тип умозаключений мы используем чаще?

Из этой статьи вы узнаете, что большинство управленческих решений принимается на основе индуктивных (вероятностных) суждений, а также о том, как грамотно использовать понимание этого в повседневной практике.

Холмс: Ватсон! Взгляните на эти звезды и расскажите мне, какой вывод, используя дедуктивный метод, вы можете сделать.

Ватсон: Я вижу на небе миллионы звезд. А раз они существуют, значит, среди них, возможно, есть и планеты. Из чего мы, в свою очередь, делаем вывод, что некоторые из них напоминают нашу Землю. Следовательно, на каких-то из них может существовать жизнь.

Холмс: Ватсон, вы – идиот. Это означает, что у нас украли палатку.

Определение понятий «индукция» и «дедукция»[1]

Возможно, вы удивились, встретив такой заголовок в блоге по менеджменту! Скоро вы поймете, какую огромную роль играет индукция в нашей жизни (не путайте понятие индукции в логике и магнитную индукцию :)).

Благодаря Артуру Конан Дойлу и его герою весь мир познакомился с дедуктивным методом. «Дедукция» из специального и известного только немногим термина превратилась в общеупотребительное и даже модное понятие.

Чего нельзя сказать об индукции. Вообще говоря, в логике существует два типа умозаключений: дедукция и индукция. В зависимости от того, существует ли между посылками, и заключением связь логического следования, можно выделить два вида умозаключений.

В дедуктивном умозаключении эта связь опирается на логический закон, в силу чего заключение с логической необходимостью вытекает из принятых посылок. Отличительная особенность такого умозаключения в том, что оно от истинных посылок всегда ведет к истинному заключению.

В индуктивном умозаключении связь посылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из посылок и может содержать информацию, отсутствующую в них. Достоверность посылок, не означает поэтому, достоверности выведенного из них индуктивно утверждения. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.

Скачать заметку в формате Word

Прочитав эти строки, я в очередной раз убедился, как важны в нашей жизни определения. См. на эту тему, например, «Определение – ключ к овладению понятием» и «Использование методов менеджмента качества в работе оптовой торговой компании». До тех пор, пока я не познакомился с определением индукции (для лучшего понимания этого термина ниже я приведу несколько примеров), я «плавал», когда встречал упоминание о нем в литературе.

Примеры дедукции

Если идет дождь, земля мокрая

Все люди смертны. Все греки – люди. Следовательно, все греки – смертны.

Примеры индукции

Аргентина является республикой; Бразилия – республика; Венесуэла – республика; Эквадор – республика. Аргентина, Бразилия, Венесуэла, Эквадор – латиноамериканские государства. Все латиноамериканские государства являются республиками.

Италия – республика; Португалия – республика; Финляндия – республика; Франция – республика. Италия, Португалия, Финляндия, Франция – западноевропейские страны. Все западноевропейские страны являются республиками.

Индукция не дает полной гарантии получения новой истины из уже имеющихся [истин]. Максимум, о котором можно говорить, – это определенная степень вероятности выводимого утверждения. Так, посылки и первого и второго индуктивного умозаключения истинны, но заключение первого из них истинно, а второго – ложно. Действительно, все латиноамериканские государства – республики; но среди западноевропейских стран имеются не только республики, но и монархии, например Англия, Бельгия и Испания.

Почувствовали разницу? Ничего не вспомнили из вашей бизнес-практики на эту тему? Не делали ли вы ранее скоропалительных выводов на основе индукции?

Вот несколько примеров «работы» индукции: «Петров вчера не справился с производственным заданием. Петров сегодня не справился с заданием. Следовательно, Петров не способен выполнять производственные задания», «В марте объем продаж вырос. В апреле объем продаж вырос. Нас ждет дальнейший рост продаж», «Ранее мы всегда действовали таким образом, и это приносило успех. Зачем же менять подходы?»

Углубим наше понимание индукции, ознакомившись с определениями из Википедии:

В экономике: индукция – вид обобщения, связанный с предвосхищением результатов наблюдений и экспериментов на основе данных опыта. В индукции данные опыта «наводят» на общее, поэтому индуктивные обобщения рассматриваются обычно как опытные истины или эмпирические законы. Изучая финансово-хозяйственную деятельность ряда типичных российских предприятий, мы можем делать, например, выводы о закономерностях развития совокупности предприятий.

В логике: полная индукция – метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности; неполная индукция – наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.

Итак, позвольте дать собственное определение для целей управления:

индукция – обобщающее суждение, основанное на нескольких прецедентах; возможно, лучшее предположение на основе имеющихся данных

Индукция и ограничивающие ментальные модели[2]

В Википедии нет определения понятия «ментальные модели». Я бы сказал, что ментальные модели – это совокупность наших знаний служащая нам для восприятия действительности. Другими словами –  это то, как мы представляем себе некий предмет, явление, событие. Через ментальные модели мы истолковываем свой опыт. Они не представляют собой факты, хотя иногда мы именно так к ним относимся.

Ментальные модели мы создаем для упрощения картины мира. Строительство ментальных моделей основано на индукции. Наблюдая за событиями, мы их обобщаем, и храним в памяти единую картину. С одной стороны, это позволяет не запоминать всё многообразие. С другой стороны, мы теряем изменчивость присущую вещам и событиям. Сначала процесс познания работает на ментальную модель, потом ментальная модель подгоняет увиденное под себя. Именно в это время и теряется гибкость и восприимчивость к новому.

Глубоко укоренившиеся в нас ментальные модели определенным образом организуют наше восприятие мира. Мы используем их, чтобы проводить различия и выбирать, что имеет для нас значение, а что – нет. И можем принять свои представления за реальность, спутать карту с той территорией, которая на ней изображена.

По каким характерным признакам можно судить о наличии ограничивающих ментальных моделей?

  • Если вы настаиваете на том, что ваши идеи полностью соответствуют реальности.
  • Если у вас узкий круг интересов, который исключает приобретение опыта.
  • Если вы не допускаете неопределенности и стараетесь как можно быстрее делать выводы.
  • Не стесняетесь делать обобщения на основании единственного случая.
  • Каждый раз, когда вас не устраивают поведение людей и ход событий, вы имеете наготове богатый запас объяснений.
  • Вину за неудачи и проблемы возлагаете на людей (не забывая при этом и себя).
  • Осмысляете происходящее в терминах прямолинейной логики «причина – следствие».
  • Никогда не проявляете любознательности.
  • Не пересматриваете своих убеждений на основе полученного опыта.

Как противостоять формированию ограничивающих ментальных моделей? Как не позволить индукции «закрыть» путь к развитию, изучению и осмыслению нового опыта, новых данных? Как сделать так, чтобы вслед за изменением мира, менялись наши ментальные модели?

  1. Почаще перечитывайте признаки ограничивающих ментальных моделей, и… делайте всё наоборот.
  2. Выделите и проанализируйте использование в речи оценочных суждений и обобщающих понятий. Все сказанное сказано кем-то. Нельзя ли поставить это под сомнение? Если вам говорят, что «у нас так принято»[3], уточните, когда и почему так было принято? Может быть, изменились условия внешней или внутренней среды, изменились исходные посылки, и выводы [сделанные на основе индукции] более не верны!?
  3. Такие выражения, как «следует», «должен», «не следует», «не можете» известны в лингвистике как модальные операторы. Заведите «капканы» для «отлавливания» модальных операторов, потому что они устанавливают границы и зачастую маскируют ограничивающие ментальные модели.
  4. Есть слова, называемые лингвистическими универсалиями, такие как: «все», «каждый», «никогда», «всегда» «никто», «любой»… Это обобщения, указывающие на отсутствие исключений, но исключения есть всегда. Вот несколько примеров: «Все делают так», «Никогда так не говори», «Мы всегда делали это так», «Никто еще никогда не возражал». Универсалии ограничивают нас, потому что, если принять их буквально, они лишают права выбора и поиска других возможностей. Услышав такое универсальное обобщение, сразу задайте вопрос о возможности исключений.
  5. Используйте выражения типа: «как мне представляется», «я так вижу», «по имеющимся данным»… Когда коллеги говорят на таком языке, споры переходят в плоскость данных и предположений; становится удобным обсуждать, как и почему сделаны именно такие выводы. Все понимают, что есть посылки и взгляды, и относятся к ним не как к фактам, а как к преломлению фактов через ментальные модели конкретных людей… 🙂

Краткий вывод для менеджеров:

индукция подменяет многообразие реальной жизни однообразными представлениями о ней; понимание этого дает вам в руки оружие против ограничивающих ментальных моделей

Индукция и теории[4]

«Никакое количество наблюдений белых лебедей не может позволить сделать вывод, что все лебеди являются белыми, но достаточно наблюдения единственного черного лебедя, чтобы опровергнуть это заключение». Нассим Талеб «Одураченные случайностью»

Ричард Фейнман, физик, Нобелевский лауреат,[5] отзываясь о философе с особо большим самомнением, говорил: «Меня раздражает вовсе не философия как наука, а та помпезность, которая создана вокруг нее. Если бы только философы могли сами над собой посмеяться! Если бы только они могли сказать: «Я говорю, что это вот так, а Фон Лейпциг считает, что это по-другому,а ведь он тоже кое-что в этом смыслит». Если бы только они не забывали пояснить, чтоэто всего лишь их лучшее предположение»

Карл Поппер, на которого широко ссылается Нассим Талеб, вторит Фейнману. Решая проблему индукции, Поппер считает, что наука не должна восприниматься так серьезно, как это принято. Есть только два типа теорий:

  1. Теории, о которых известно, что они являются неверными, поскольку они были проверены и, соответственно, отвергнуты (он называет их фальсифицированными).
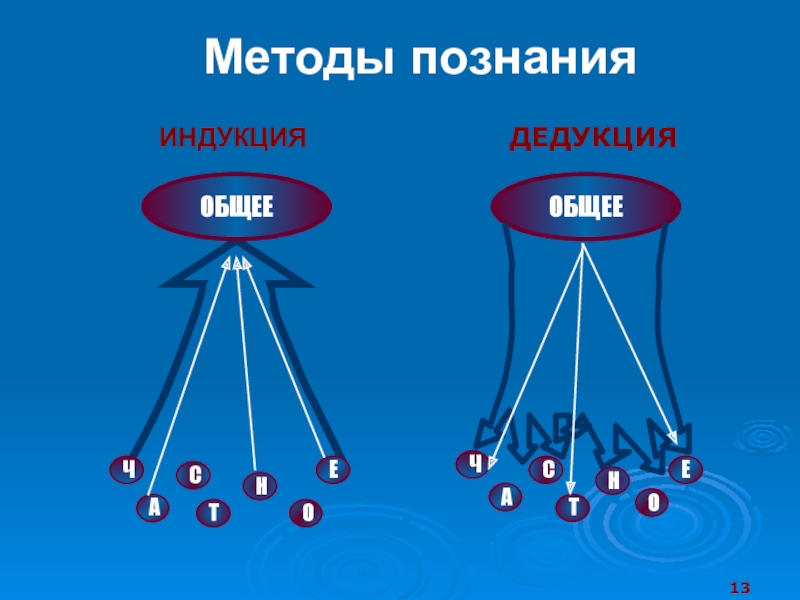
  2. Теории, о которых ещё не известно, что они неправильны, они ещё не фальсифицированы, но рискуют стать таковыми.

Теория, которая выпадает из этих двух категорий – не является теорией. Теория, которая не предоставляет набор условий, при которых она считалась бы неправильной, должна быть названа шарлатанством. Почему? Потому, что астролог всегда может найти причину приспособиться к прошлому событию, говоря, что Марс был, вероятно, на линии, но не слишком долго 🙂 В самом деле, различие между ньютоновской физикой, которая была фальсифицирована теорией относительности Эйнштейна, и астрологией заключается в следующей иронии. Ньютоновская физика научна потому, что позволяет нам фальсифицировать её, поскольку мы знаем, что она неправильна, в то время как астрология – нет, потому, что она не предлагает условия, при которых мы могли бы отвергнуть её. Астрология не может быть опровергнута, вследствие вспомогательных гипотез, которые входят в игру. Этот пункт находится в основе разграничения между наукой и ерундой.

Для Поппера вопрос знания не так много имеет дело с тем, что мы знаем, как с тем, что мы не знаем. Его знаменитая цитата: Они – люди со смелыми идеями, но высоко критичные к этим, их собственным идеям, они пытаются определить, являются ли их идеи правыми, пробуя сначала определить,  возможно ли, что они не неправильны. Они работают со смелыми догадками и серьезными попытками опровержения своих собственных догадок.

«Они» ­– это ученые. Но они могли быть кем угодно [для нас интересно, если – менеджерами].

Память людей является машиной по производству индуктивных выводов. Задумайтесь о воспоминаниях: что легче вспомнить – набор случайных фактов, слепленных вместе, или историю, некую последовательность логических связей? Причинно-следственные связи легче закрепляются в памяти. В этом случае нашему мозгу приходится проделать меньшую работу для сохранения информации. Ее объем меньше. Это очень удобно, так как общее занимает в памяти гораздо меньше места, чем набор частностей. Вот только в результате такого сжатия сокращается степень наблюдаемой случайности.

Краткий вывод для менеджеров

индукция формирует стереотипы, которыми имеет смысл пользоваться, пока не появился хотя бы один факт, опровергающий первоначальное предположение; когда же такой факт выявлен, вместо того, чтобы упорствовать, и «подгонять» факты под стереотипы, попытайтесь выдвинуть иную гипотезу, объясняющую  как прежние, так и новые факты

Индукция и методы менеджмента качества[6]

Типичные примеры индукции – сводки[7] данных или статистики на основе исходных данных: среднее значение (µ), медиана, стандартное отклонение (σ). Вместо того, чтобы изучать множество значений, мы ограничиваемся лишь небольшим набором статистик (например, µ ± σ). Преимущества очевидны: статистики неплохо описывают выборку значений. Недостатки не так заметны: за средними значениями могут прятаться значительные нежелательные «выбросы».

На индукции основано применение контрольных карт Шухарта: если управляемый процесс ранее был в неких рамках, то и в будущем мы считаем, что с определенной вероятностью он будет в таких же рамках (рис. 1а). С другой стороны, прогноз поведения неуправляемого процесса затруднен (рис. 1б).

Рис. 1. Динамика среднего значения и стандартного отклонения во времени в присутствии общих (а) или специальных (б) причин вариаций.

* * *

Возвращаясь к методу Шерлока Холмса с прискорбием должен сообщить, что [на мой взгляд / в соответствии с моими ментальными моделями :)] он использовал индукцию, а вовсе не дедукцию! Изучая факты, Холмс делал выводы, имеющие вероятностную природу. Виртуозно обнаруживая мельчайшие «зацепки», он выстраивал гипотезы (вряд ли, одну), затем проверял их, и лишь затем, являл миру свое объяснение фактов.

Практические выводы для менеджеров:

а) подавляющее большинство умозаключений [и решений, принимаемых на их основе] имеют индуктивную природу, то есть их истинность не абсолютна, а вероятностна;

б) необходимо отдавать себе отчет, что мир и наши представления о нем – не одно и то же; не сдавайтесь на милость жестким [ограничивающим] ментальным моделям, развивайте их, будьте любознательны;

в) «черный лебедь» [факт, не укладывающийся в господствующую систему] – повод пересмотреть стереотипы, и выдвинуть новые гипотезы, а не «латать» прежние.

[1] В этом разделе цитируется учебное пособие А.А.Ивина ЛОГИКА.

[2] В этом разделе используются идеи из Джозеф О’Коннор, Иан Макдермотт «Искусство системного мышления»

[3] На тему «у нас так принято» есть любопытная притча (цитируется с сокращениями по http://www.litvar.ru/a-potomu-chto-zdes-tak-prinyato-eksperiment/):

Возьмём металлическую клетку, к потолку подвесим банан, под бананом поставим стремянку, а в клетку запустим пять обезьян. Наступает момент, когда какой-нибудь обезьяне захочется кушать. Она лезет к банану, но мы с помощью пожарного брандспойта сбиваем её со стремянки ледяной водой, а заодно окатываем и всех остальных. Какое-то время они сидят ошалевшие, но наступает момент, когда томимая голодом обезьяна опять делает попытку добраться до банана. Повторяем процедуру… И так раза три-четыре. Кончается дело тем, что когда беспокойное животное опять пытается подойти к стремянке, остальные четверо его от неё оттаскивают и банально бьют.

Убираем из клетки беспокойную обезьяну и добавляем туда “свежую”. Проходит какое-то время, и она делает попытку добраться до банана. Четыре бдительные обезьяны, оставшиеся с прошлого раза, оттаскивают её и… бьют, хотя на этот раз никого не обливали. Разумеется, бедное животное не может понять за что, поэтому делает ещё одну попытку. Его опять бьют, но уже сильнее. В конечном итоге и эта обезьяна присоединяется к остальным в бездеятельном созерцании еды.

Убираем из клетки ещё одну находившуюся там с самого начала обезьяну и сажаем новую “свежую”. Результат предсказуем – она лезет за бананом, остальные вскакивают, оттаскивают и бьют. При этом с особым зверством бьёт та обезьяна, которую не обливали. Ситуация повторяется n-ное количество раз, где “n” зависит от сообразительности животного. Опять обезьяны просто сидят и смотрят на банан.

Опять вытаскиваем обезьяну из первого “эшелона” и снова добавляем “свежую”…  В итоге получаем ситуацию, когда в клетке сидят пять ни разу не облитых обезьян, но ни одна из них не делает попыток дотянуться до банана. Почему? А потому, что здесь так принято.

[4] А этот раздел написан по мотивам книги Нассима Талеба «Одураченные случайностью».

[5] Если вы имеете отношение к физике, то вполне могли слышать о «Фейнмановских лекциях по физике» – замечательном, очень хорошо написанном курсе.

[6] В этом разделе использованы идеи из книги Д. Уилер, Д. Чамберс «Статистическое управление процессами».

[7] Сводка – представление большого числа исходных данных одним числом.

Математическая индукция

Математическая индукция — это особый способ доказательства. В нем всего 2 ступени:

  • Шаг 1. Покажите, что это верно для первого
  • Шаг 2. Покажите, что если любое из истинно, то следующее истинно

Тогда все верны

Вы слышали об «эффекте домино»?

  • Шаг 1. Первое падение домино
  • Шаг 2.Когда выпадает любое домино, следующее домино выпадает

Итак . .. все домино упадут!

Так работает математическая индукция.

В мире чисел мы говорим:

  • Шаг 1. Покажите, что это верно для первого случая, обычно n = 1
  • Шаг 2. Покажите, что если n = k верно, то n = k + 1 также верно

Как это сделать

Шаг 1 обычно прост, нам просто нужно доказать, что он верен для n = 1

Шаг 2 лучше всего выполнить так:

  • Предположим, что верно для n = k
  • Докажите, что верно для n = k + 1 (мы можем использовать случай n = k как факт .)

Это все равно что сказать «ЕСЛИ мы можем заставить домино упасть, упадет ли следующая?»

Шаг 2 часто может быть сложным , нам, возможно, придется использовать творческие уловки, чтобы заставить его работать!

Как в этом примере:

Пример: 3

n −1 делится на 2?

Это правда? Давайте узнаем.

1. Покажите, что это верно для n = 1

3 1 −1 = 3−1 = 2

Да 2 делится на 2.Это было просто.

3 1 −1 верно

2. Предположим, что это верно для n = k

3 k −1 верно

(Погодите! Откуда мы это знаем? Мы этого не делаем!
Это предположение … что мы рассматриваем
как факт для остальной части этого примера)

Теперь докажем, что 3 k + 1 −1 делится на 2

3 k + 1 также 3 × 3 k

А затем разделите 3 × на 2 × и 1 ×

И каждое из них кратно 2

Потому что:

  • 2 × 3 k делится на 2 (мы умножаем на 2)
  • 3 k −1 верно (мы сказали, что в предположении выше)

Итак:

3 k + 1 −1 верно

СДЕЛАНО!

Вы видели, как мы использовали случай 3 k −1 как истинный , хотя мы этого и не доказали? Это нормально, потому что мы полагаемся на Domino Effect . ..

… мы спрашиваем , если упадет любое домино, упадет ли следующий ?

Итак, мы принимаем это как факт (временно), что домино « n = k » падает (т.е. 3 k −1 верно), и посмотрим, означает ли это « n = k + 1 ». «Домино тоже упадет.

Уловки

Я уже говорил, что нам часто нужно использовать творческие уловки.

Обычный трюк состоит в том, чтобы переписать случай n = k + 1 на 2 части:

  • одна часть представляет собой случай n = k (который предполагается верным)
  • затем можно проверить другую часть, чтобы убедиться, что она также верна

Мы сделали это в примере выше, а вот еще один:

Пример: сложение нечетных чисел

1 + 3 + 5 +… + (2n − 1) = n 2

1. Покажите, что это верно для n = 1

1 = 1 2 верно

2. Предположим, что это верно для n = k

1 + 3 + 5 + … + (2k − 1) = k 2 верно
(Предположение!)

Теперь докажите, что это верно для «k + 1»

1 + 3 + 5 + … + (2k − 1) + (2 (k + 1) −1) = (k + 1) 2 ?

Мы знаем, что 1 + 3 + 5 +… + (2k − 1) = k 2 (предположение выше), поэтому мы можем сделать замену для всех членов, кроме последнего:

к 2 + (2 (k + 1) −1) = (k + 1) 2

Теперь разверните все термины:

к 2 + 2 к + 2 — 1 = к 2 + 2 к + 1

И упростить:

к 2 + 2 к + 1 = к 2 + 2 к + 1

Они такие же! Так что это правда.

Итак:

1 + 3 + 5 +… + (2 (k + 1) −1) = (k + 1) 2 верно

СДЕЛАНО!

Твоя очередь

А теперь еще два примера , на которых вы можете попрактиковаться.

Сначала попробуйте их сами, а затем посмотрите наше решение ниже.

Пример: треугольные числа

Треугольные числа — это числа, которые могут образовывать треугольный точечный узор.

Докажите, что n-ое треугольное число равно:

Т п = п (п + 1) / 2

Пример: сложение чисел куба

Числа куба — это кубы натуральных чисел

Докажите, что:

1 3 + 2 3 + 3 3 +… + n 3 = ¼n 2 (n + 1) 2

. . . . . . . . . . . . . . . . . .

Пожалуйста, не читайте решения, пока не попробуете сами, это единственные вопросы на этой странице, над которыми вы можете попрактиковаться!

Пример: треугольные числа

Докажите, что n-ое треугольное число равно:

Т п = п (п + 1) / 2

1. Показать, что это правда для n = 1

T 1 = 1 × (1 + 1) / 2 = 1 истинно

2. Предположим, что это верно для n = k

T k = k (k + 1) / 2 Верно (предположение!)

Теперь докажите, что это верно для «k + 1»

Т к + 1 = (к + 1) (к + 2) / 2?

Мы знаем, что T k = k (k + 1) / 2 (предположение выше)

T k + 1 имеет дополнительный ряд (k + 1) точек

Итак, T k + 1 = T k + (k + 1)

(к + 1) (к + 2) / 2 = к (к + 1) / 2 + (к + 1)

Умножьте все члены на 2:

(к + 1) (к + 2) = к (к + 1) + 2 (к + 1)

(к + 1) (к + 2) = (к + 2) (к + 1)

Они такие же! Так что правда .

Итак:

T k + 1 = (k + 1) (k + 2) / 2 истинно

СДЕЛАНО!

Пример: сложение чисел куба

Докажите, что:

1 3 + 2 3 + 3 3 + … + n 3 = ¼n 2 (n + 1) 2

1. Покажите, что это верно для n = 1

1 3 = ¼ × 1 2 × 2 2 верно

2. Предположим, что это верно для n = k

1 3 + 2 3 + 3 3 + … + k 3 = ¼k 2 (k + 1) 2 верно (предположение!)

Теперь докажите, что это верно для «k + 1»

1 3 + 2 3 + 3 3 + … + (k + 1) 3 = ¼ (k + 1) 2 (k + 2) 2 ?

Мы знаем, что 1 3 + 2 3 + 3 3 +… + k 3 = ¼k 2 (k + 1) 2 (предположение выше), поэтому мы можем заменить все, кроме последнего члена:

¼k 2 (k + 1) 2 + (k + 1) 3 = ¼ (k + 1) 2 (k + 2) 2

Умножьте все члены на 4:

к 2 (к + 1) 2 + 4 (к + 1) 3 = (к + 1) 2 (к + 2) 2

Все термины имеют общий множитель (k + 1) 2 , поэтому его можно отменить:

к 2 + 4 (к + 1) = (к + 2) 2

И упростить:

к 2 + 4 к + 4 = к 2 + 4 к + 4

Они такие же! Так что это правда.

Итак:

1 3 + 2 3 + 3 3 + … + (k + 1) 3 = ¼ (k + 1) 2 (k + 2) 2 верно

СДЕЛАНО!

Виды и способы индукции труда

Что такое индукция? Мы говорим о стимулировании труда как о способе искусственного запуска процесса труда. Обычно это происходит, когда по медицинским показаниям требуется, чтобы ребенок родился раньше или мать не забеременела.

Когда роды должны начаться, есть несколько способов подойти к этому. Многие люди с удивлением обнаруживают, что существует множество различных типов индукции. Ни один метод не подойдет для каждой беременности.

Разрыв мешка с водой

Используя предмет, называемый амнихук, ваш практик сделает крошечный надрыв в мешке с водой. Это приведет к тому, что вода начнет вытекать. Поскольку в сумке нет нервов, это должно быть не более болезненно, чем обычный вагинальный осмотр.Считается, что при разрыве сумки обычно начинаются схватки.

Преимущества: Никакие химические вещества могут не понадобиться, вы сохраняете большую мобильность, чем если бы вам требовалась капельница.

Недостатки: Схватки могут не начаться, и тогда это приведет к другим вмешательствам, таким как использование питоцина. Это может также вызвать инфекцию мешка, подушка для ребенка теперь удалена, и редко, но возможно, выпадение пуповины, требующее немедленного кесарева сечения.Взаимодействие с другими людьми

Разрыв амниотического мешка также требует, чтобы у вас родился ребенок в течение определенного периода времени, в зависимости от обстоятельств и убеждений вашего практикующего. Лучше использовать амниотомию с другими методами индукции.

Питоцин

Это искусственная версия гормона окситоцина организма. Он вводится через капельницу и используется, чтобы вызвать схватки. Количество используемого питоцина будет зависеть от того, как ваше тело принимает его. Как правило, количество увеличивают каждые 10-30 минут, пока не будет достигнута хорошая картина сокращения.Иногда это делается в сочетании с разбиванием мешка с водой.

Преимущества: Немного легче контролировать, чем, скажем, разорвать воду, потому что лекарство можно остановить, перекрыв капельницу. Это не обязывает вас иметь ребенка. Его можно выключить или остановить, чтобы дать маме отдохнуть или даже пойти домой.

Недостатки: Может вызывать дистресс плода, не может вызывать схваток. Может вызвать слишком частые или длительные схватки.Из-за потенциальных рисков FDA заявило, что это лекарство не должно использоваться для индукции по соображениям удобства или планирования.

Гели / свечи с простагландином

Они используются чаще, когда шейка матки неблагоприятна, что означает, что она расширена менее чем на 3 сантиметра, твердая, задняя часть, не стерта, почти не стерта или любая комбинация вышеперечисленного. Используя Bishop’s Score, ваш практик решит, лучше ли это начать.Это можно использовать отдельно или чаще всего за 12 или более часов до использования Pitocin.

Часто его дают более одного раза в течение вечера / ночи. Суппозиторий или тампоноподобное вещество будет помещено в шейку матки или рядом с ней во время влагалищного исследования.

Преимущества: Чем более благоприятна ваша шейка матки, тем меньше вероятность того, что индукция «потерпит неудачу». Иногда это все, что нужно, иногда также используется питоцин. Это можно сделать амбулаторно.Это не обязывает вас заводить ребенка.

Недостатки: Требуется больше времени для начала активных родов, может нервничать, если политика вашего учреждения такова, что вы должны оставаться в больнице в течение периода ожидания. Иногда мама испытывает тошноту или головные боли, которые нельзя контролировать так же, как питоцин, но они, как правило, более легкие. К некоторым формам простагландинов теперь прикреплены завязки, которые делают их съемными в случае опасных сокращений.

Мизопростол (Cytotec)

Это таблетка, которую можно принимать внутрь или положить рядом с шейкой матки.Его применяют чаще, когда шейка матки не очень благоприятна.

Преимущества: Нет привязки к линии IV. Его можно использовать самостоятельно. Чем более благоприятна ваша шейка матки, тем меньше вероятность того, что индукция «потерпит неудачу». Не так грязно, как потенциально могут быть свечи. Не обязывает вас заводить ребенка.

Недостатки: Может потребоваться использование Питоцина или других средств дополнительно. Это может вызвать очень быстрые роды. Недавняя мысль заключается в том, что это недопустимый вариант для матерей, которые пытаются использовать VBAC; обсудите это со своим врачом.Взаимодействие с другими людьми

Домашняя индукция

Есть несколько способов вызвать роды в домашних условиях. Они варьируются от стимуляции сосков и полового акта до приема трав и таких веществ, как касторовое масло.

Любой метод, который вы хотите использовать для индукции в домашних условиях, следует обсудить со своим врачом, прежде чем пытаться его использовать.

Многие женщины будут клясться одним или всеми из них, однако не все женщины будут начинать роды с помощью любого метода индукции.

  • Ходьба
  • Половое сношение
  • Оргазм с партнером или без
  • Стимуляция сосков
  • Определенные продукты (т.е. острая пища, масляные салаты)
  • Едет на ухабистой машине
  • Напряженная деятельность
  • Визуализация
  • Касторовое масло
  • Некоторые травы и гомеопатические средства (клопогон черный и синий, Caulophyllum и т. Д.)

Преимущества: Обычно меньше вмешательств и меньше вероятность кесарева сечения. Обычно, если ваше тело и ребенок не готовы, это не сработает, но это зависит от метода. Это легче сделать, и большинство мам не так сильно беспокоит их.

Недостатки: Могут быть серьезные последствия, особенно если вы еще не доношенный ребенок и ваш ребенок еще не готов к рождению. Многие из сказок старых жен, такие как касторовое масло, обычно не работают и могут иметь потенциальные осложнения, включая такие вещи, как окрашивание мекония, дистресс плода и т.д.

Факторы, влияющие на сокращение занятости

Часто индукция проводится по причине того, что истек срок родов. Недавно было проведено несколько исследований, которые показывают, что сроки родов на самом деле должны быть длиннее 40 недель. Часто проводятся ненужные индукционные курсы.

Иногда их делают, потому что женщина пытается родить через естественные родовые пути после кесарева сечения (VBAC) или у нее есть подозрение на крупный ребенок. Многие исследования показали, что это не обязательно веские причины для индукции, особенно если шейка матки еще не созрела.

Некоторые женщины боятся индукции по разным причинам, включая повышенную вероятность кесарева сечения, повышенную потребность в обезболивающих или опасение причины индукции, особенно если возникает вопрос о здоровье ребенка.

Будет ли индукция более болезненной, чем естественные роды? Не обязательно, это больше зависит от ваших причин для индукции, типа индукции и от того, ограничена ли ваша мобильность. Многие женщины могут быть побуждены и все еще выполняют свои планы на немедикаментозные роды, хотя они могут ожидать определенных изменений в своих планах родов.

Слово Verywell

Если предлагается индукция, соберите факты и информацию и задавайте вопросы.Почему это предлагается? Как бы это было предпринято? Что будет, если это не сработает? Что произойдет, если вы ничего не сделаете?

Нет единого мнения относительно использования индукции, хотя для этого есть свое время и место, как и любое вмешательство по медицинским причинам, хотя даже эксперты не могут прийти к единому мнению во всех случаях, когда индукция была бы лучшим выбором.

Доказательство индукцией

Доказательство индукцией Доказательства по индукции Доказательство по индукции похоже на обычное доказательство, в котором каждый шаг должно быть оправдано. Однако в нем используется хитрый прием, который позволяет вам чтобы доказать утверждение о произвольном числе n, сначала доказав это верно, когда n равно 1, а затем предполагая, что это верно для n = k и показывая это верно для n = k + 1. Идея в том, что если вы хотите показать это кому-то может подняться на n-й этаж пожарной лестницы, вам нужно только показать, что вы можете подняться по лестнице на пожарную лестницу (n = 1), а затем показать, что умеешь подниматься по лестнице с любого уровня пожарной лестницы (n = k) на следующий уровень (n = k + 1).

Если вы сделали доказательство по индукции до того, как вас могут попросить предположим случай n-1 и покажем случай n, или предположим случай n и покажем случай n + 1. Это то же самое, что я объясняю здесь, но я используйте другую букву, потому что я думаю, это позволяет избежать путаницы, когда пытаясь выяснить, в чем заключается каждый случай.

Пример 1. Докажите 1 + 2 + … + n = n (n + 1) / 2, используя доказательство по индукции.

n = 1: 1 = 1 (2) / 2 = 1 проверка.

Предположим, что выполняется n = k: 1 + 2 +… + k = k (k + 1) / 2 (индукционная гипотеза)
Показать n = k + 1: 1 + 2 + … + k + (k + 1) = (k + 1) ((k + 1) +1) / 2
Я просто подставляю k и k + 1 в формулу, чтобы получить эти строки. Обратите внимание, что я записываю то, что хочу доказать.

Теперь я начну с левой части уравнения, которое хочу показать. и продолжаем, используя предположение индукции и алгебру, чтобы достичь правая часть уравнения. 1 + 2 + … + (к + 1) = 1 + 2 + … + к + (к + 1)
= k (k + 1) / 2 + (k + 1) по гипотезе индукции
= (k (k + 1) +2 (k + 1)) / 2 на 2/2 = 1 и распределение деления по сложению
= (k + 2) (k + 1) / 2 по распределению умножения над сложением
= (k + 1) (k + 2) / 2 по коммутативности умножения

QED

Пример 2: Докажите, что если P1 P2…Pn — коллинеарные точки в пространстве, удовлетворяющие аксиомам инцидентности и промежуточности, так что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 .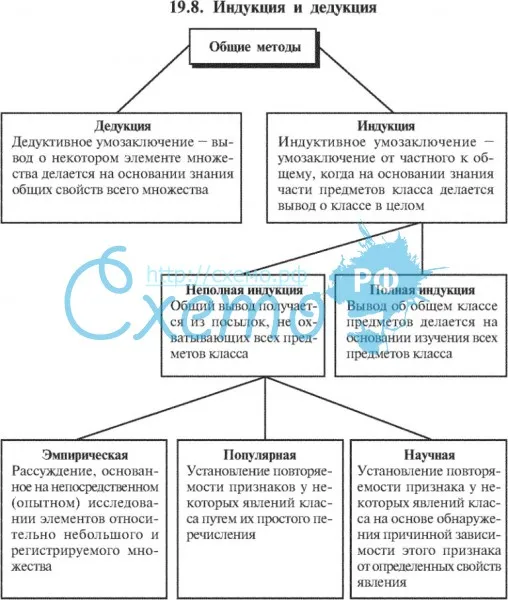 .. (n-1), тогда Pj находится между P1 и Pn для любого j = 2 … (n-1).

Это другой вид доказательства по индукции, потому что в нем нет смысла. пока n = 3. Итак, мы начинаем с n = 3, а затем показываем, что если n = k, мы получаем n = (k + 1), таким образом доказывая утверждение для n = 3,4,5,6, …

n = 3: P2 находится между P1 и P3, подразумевает, что P2 находится между P1 и P3.Сделанный

Предположим, что n = k: , если P1 P2 … Pk коллинеарные точки такой, что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 … (k-1), тогда Pj находится между P1 и Pk для любого j = 2 … (k-1). Гипотеза индукции.

Показать n = k + 1: , если P1 P2 … P (k + 1) коллинеарные точки такой, что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 … k, тогда Pj находится между P1 и P (k + 1) для любого j = 2 … (k).

K точек P1, P2, … P (k-1) P (k + 1) удовлетворяют условиям индукции гипотеза, чтобы мы знали Pj находится между P1 и P (k + 1) для любого j = 2. .. (к-1).

K точек P1, P3, P4 … Pk P (k + 1) также удовлетворяют условиям индукции гипотеза, поэтому мы знаем, что Pj находится между P1 и P (k + 1) для любого j = 3 … (k).

QED

Пример 3: Докажите, что любое пространство, удовлетворяющее аксиомам инцидентности и Промежуток, содержащий точку, имеет бесконечное количество различных коллинеарные точки.

Если я могу показать, что пространство содержит n точек для любого числа n, тогда он должен иметь бесконечное количество точек.Так Я проведу доказательство индукцией по количеству точек n.

n = 1: Содержит ли пробел хотя бы одну точку? Да, это делает гипотеза («которая содержит точку»)

Предположим, мы нашли n = k коллинеарных точек (гипотеза индукции)
Покажите, что мы можем найти n = k + 1 коллинеарных точек. Нам нужно найти еще одну точку.

А теперь нарисуем картинку. Если мы поставим все точки на линию тогда легко добавить еще одну точку в конце. Сделать это проще если баллы в порядке. Другими словами было бы проще доказать: любое пространство, удовлетворяющее Аксиомам инцидентности и Промежуток, содержащий точку, имеет бесконечное количество различных коллинеарные точки P1, P2, … такие, что каждая Pi находится между P (i + 1) и P (i-1) для i> 1. Итак, мы изменим нашу гипотезу индукции.

Предположим, что n = k: , что у нас есть n = k коллинеарных точек P1, P2, … Pk таких, что P2 находится между P1 и P3, P3 находится между P4 и P2… P (k-1) находится между P (k-2) и Pk. (Новая гипотеза индукции)

Показать n = k + 1: что у нас есть n = k + 1 коллинеарных точек P1, P2, … P (k + 1) таких, что P2 находится между P1 и P3, P3 находится между P4 и P2, … P (k) находится между P (k-1) и P (k + 1).

По предположению индукции мы имеем k коллинеарных точек. Находим k + 1 точку, используя аксиому B2, которая гласит, что при B = P (1) и D = Pk мы можем найти новая точка E = P (k + 1) такая, что Pk находится между P (1) и P (k + 1). *

Теперь нам нужно показать, что P (k + 1) отличается от Pj для любого j = 1,2…к.

По примеру 2. мы знаем, что Pj находится между P1 и Pk для j = 2,3 … k-1. *

Однако P (k) находится между P1 и P (k + 1), поэтому по аксиоме B3 P (k + 1) не может быть Pj для j = 2,3 … k-1.

Поскольку P (k + 1) уже отличался от P1 и Pk, мы закончили.

QED?

В этом доказательстве есть две ошибки! Когда мы цитировали Пример 2, мы могли сделать это, только если k было больше или равно 3! Также на самом первом шаге мы предполагаем, что k было больше или равно 2! См. * В доказательстве.

Затем мы должны выполнить эти случаи в начале в дополнение к n = 1.

n = 2: Согласно аксиоме I3 существуют три точки, которые не являются коллинеарными. Пусть P1 и P2 — две из этих точек. Эти пункты «по порядку» потому что их всего двое.

n = 3: В случае n = 2 мы знаем, что у нас есть две коллинеарные точки P1 и P2.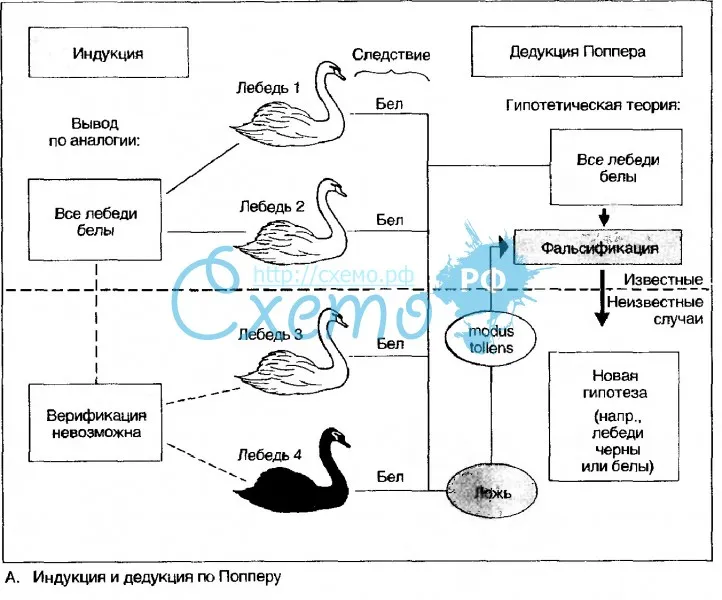 По аксиоме B3 мы можем найти P3 такое, что P2 находится между P1 и P3. Они уже в порядке только Axiom B3.(n-1) используя определение производная.

3) Докажите, что пространство с n точками чьи прямые — это любая пара различных точек удовлетворяет аксиомам инцидентности.

4) Докажите, что в пространстве, удовлетворяющем аксиомам инцидентности и между двумя точками A и B бесконечно между ними много точек.

Математическая индукция — Темы в предварительном исчислении

27

Принцип математической индукции

НАТУРАЛЬНЫЕ ЧИСЛА — это подсчет числа: 1, 2, 3, 4 и т. д.Математическая индукция — это метод доказательства утверждения — теоремы или формулы — которое утверждается примерно на каждые натуральных чисел.

Под «каждым» или «всеми» натуральными числами мы подразумеваем любое имя, которое мы называем.

Например,

1 + 2 + 3 +. . . + n = ½ n ( n + 1).

Утверждается, что сумма последовательных чисел от 1 до n дается формулой справа. Мы хотим доказать, что это будет верно для n = 1, n = 2, n = 3 и так далее. Теперь мы можем проверить формулу для любого с заданным номером , скажем, n = 3:

.

1 + 2 + 3 = ½ · 3 · 4 = 6

— это правда. Это также верно для n = 4:

1 + 2 + 3 + 4 = ½ · 4 · 5 = 10.

Но как мы можем доказать это правило для через каждое значение из n ?

Метод доказательства следующий.Мы показываем, что , если утверждение — правило — верно для любого конкретного числа k (например, 104), то оно также будет верно для его преемника, k + 1 (например, 105). Затем мы показываем, что утверждение будет истинным для 1. Из этого следует, что утверждение будет истинным для 2. Следовательно, оно будет истинным для 3. Оно будет истинным для любого натурального числа, которое мы назовем.

Это называется принципом математической индукции.

Если
1) , когда утверждение верно для натурального числа n = k ,
, то оно также будет верно для его преемника, n = k + 1;
и
2) утверждение верно для n = 1;
, то утверждение будет истинным для любого натурального числа n .

Чтобы доказать утверждение по индукции, мы должны доказать пункты 1) и 2) выше.

Гипотеза шага 1) — « Утверждение верно для n = k » — называется предположением индукции или гипотезой индукции. Это то, что мы, , предполагаем, , когда доказываем теорему по индукции.

Пример 1. Докажите, что сумма первых n натуральных чисел дается следующей формулой:

1 + 2 + 3 +.. . + n = n ( n + 1)
2 		.

Доказательство . Мы выполним шаги 1) и 2) выше. Во-первых, мы предположим, что , что формула верна для n = k ; то есть примем:

1 + 2 + 3 +. . . + к = к ( к + 1)
2 		.(1)

Это предположение индукции. Предполагая это, мы должны доказать, что формула верна для ее преемника, n = k + 1. То есть мы должны показать:

1 + 2 + 3 +. . . + ( к + 1) = ( к + 1) ( к + 2)
2 		. (2)

Для этого мы просто добавим следующий член ( k + 1) к обеим сторонам предположения индукции, линия (1):

Это строка (2), это первое, что мы хотели показать.

Далее мы должны показать, что формула верна для n = 1. У нас есть:

1 = ½ · 1 · 2

— это правда. Теперь мы выполнили оба условия принципа математической индукции. Таким образом, формула верна для любого натурального числа.

(В Приложении к арифметике мы устанавливаем эту формулу напрямую.)

Пример 2. Докажите, что это правило экспонент верно для любого натурального числа n :

.

( ab ) n = a n b n .

Доказательство . Опять же, мы начинаем с , предполагая, что истинно для n = k ; то есть мы предполагаем:

( ab ) k = a k b k . . . . . . . . (3)

Используя это предположение, мы должны показать, что правило верно для его преемника: n = ( k + 1). Мы должны показать:

( ab ) k + 1 = a k + 1 b k + 1 . . . . . . . (4)

(При использовании математической индукции ученик всегда должен писать именно то, что должно быть показано.)

Теперь, учитывая предположение, строку (3), как мы можем из нее построить строку (4)?

Просто умножив обе стороны прямой (3) на ab :

( ab ) k ab = a k b k ab
= a k a b k b
, поскольку порядок факторов не имеет значения,
= а к + 1 b к + 1 .

Это строка (4), которую мы хотели показать.

Итак, мы показали, что если теорема верна для любого конкретного натурального числа k , то она верна и для его преемника, k + 1.

Затем мы должны показать, что правило верно для n = 1; то есть

( ab ) 1 = a 1 b 1 .

Но ( ab ) 1 = ab ; и a 1 b 1 = ab .

Следовательно, это правило верно для любого натурального числа n .

Пример 3. Сумма последовательных кубиков. Докажите этот замечательный арифметический факт:

1 3 + 2 3 + 3 3 +. . . + n 3 = (1 + 2 + 3 +.. . + n ) 2 .

«Сумма n последовательных кубов равна квадрату
суммы первых n чисел».

Другими словами, согласно Примеру 1:

1 3 + 2 3 + 3 3 +. . . + n 3 = n ² ( n + 1) ²
4

Доказательство .Для удобства обозначим сумму до n через S ( n ). Таким образом, мы предполагаем, что формула верна для n = k ; то есть

S ( к ) = к ² ( к + 1) ²
4 		(1)
Теперь мы должны показать, что формула верна и для n = k + 1; тот
S ( k + 1) = ( к + 1) ² ( к + 2) ²
4 		(2)
Для этого добавьте следующий куб к S ( k ), строка (1):
S ( k + 1) = S ( к ) + ( к + 1) 3
= к ² ( к + 1) ²
4 		+ ( к + 1) 3
= k ² ( k + 1) ² + 4 ( k + 1) ³
4
= ( к + 1) ² [ к ² + 4 ( к + 1)]
4
— принимая ( k + 1) 2 как общий множитель,
= ( к + 1) ² ( к ² + 4 к + 4)
4
= ( к + 1) ² ( к + 2) ²
4

Это строка (2), которую мы хотели показать.

Наконец, мы должны показать, что формула верна для n = 1.

1 3 = 1² · 2²
4
1 = 1 · 4
4

— это правда. Таким образом, формула верна для любого натурального числа.

В Приложении к арифметике мы прямо показываем, что это правда.

Задача 1. Согласно принципу математической индукции, чтобы доказать утверждение, которое утверждается в отношении каждого натурального числа n , нужно доказать две вещи.

а) Что первое?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

Если утверждение верно для n = k , то оно будет верно для его преемника, k + 1.

б) Что второе?

Утверждение верно для n = 1.

c) Часть a) содержит предположение индукции. Что это?

Утверждение верно для n = k .

Проблема 2.Пусть S ( n ) = 2 n — 1. Вычислите

а) S ( к ) = 2 к — 1

б) S ( к + 1) = 2 ( k + 1) — 1 = 2 k + 2 — 1 = 2 k + 1

Задача 3. Сумма первых n нечетных чисел равна n-му квадрату .

1 + 3 + 5 + 7 +. . . + (2 n — 1) = n 2 .

a) Чтобы доказать, что с помощью математической индукции, какова будет индукция
а) предположение?

Утверждение верно для n = k :

1 + 3 + 5 + 7 +. . . + (2 к — 1) = к 2 .

б) Что мы должны показать на основании этого предположения?

Утверждение верно для его преемника, k + 1:

.

1 + 3 + 5 + 7 +. . . + (2 k — 1) + 2 k + 1 = ( k + 1) ².

c) Покажи это.

При добавлении 2 k + 1 к обеим сторонам предположения индукции:

1 + 3 + 5 + 7 +. . . + (2 к — 1) + 2 к + 1 = к ² + 2 к + 1
= ( к + 1) 2

г) Что мы должны показать, чтобы завершить доказательство математической индукцией?

Утверждение верно для n = 1.

д) Покажи это.

1 = 1 2

Задача 4. Докажите математической индукцией:

Если мы обозначим эту сумму как S ( n ), тогда предположим, что формула верна для n = k ; то есть предположим, что

S ( к ) = к
2 к + 1 		.

Теперь покажите, что формула верна для n = k + 1; то есть показать:

S ( к + 1) = к + 1
2 к + 3 		.

Начало:

Далее,

Формула верна для n = 1:

Следовательно, это верно для всех натуральных чисел.

Содержание | Дом

Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]


Искусственные роды — какие есть возможности?

Если вы решите использовать искусственные роды, их тип будет зависеть от ваших конкретных обстоятельств.Процесс будет разным для всех. Иногда вам может потребоваться комбинация методов, чтобы начать роды. Вы обсудите эти различные методы со своим врачом, когда решите, проводить ли искусственные роды.

Принятие решения о принудительных родах

Если вы опаздываете, вы можете подождать и посмотреть, начнутся ли роды естественным путем. Однако, если есть вероятность, что вы или ваш ребенок подвержены риску, вам может потребоваться рассмотреть возможность искусственных родов до срока.

Принимая решение, обсудите риски и преимущества со своим врачом.Не бойтесь задавать много вопросов, например:

  • Зачем нужна индукция?
  • Как это повлияет на меня и моего ребенка?
  • Что будет, если у меня не будет индукции?
  • Какие процедуры используются и как вы будете заботиться обо мне и моем ребенке?

Есть несколько проблем со здоровьем, которые вам, возможно, следует учитывать. Например, существует более высокий риск мертворождения или других проблем, если ваш ребенок родился не ранее 42 недель, и повышенный риск заражения, если ваши воды отошли более чем за 24 часа до начала родов.

Варианты стимулирования родов

Есть разные способы вызвать роды. При осмотре шейки матки ваш врач или акушерка выберут для вас лучший вариант. Вам может понадобиться сочетание разных стратегий. Вам нужно будет предоставить письменное согласие на процедуру.

Различные способы стимулирования труда:

Подметание мембран

Во время влагалищного обследования акушерка или врач совершает круговые движения пальцем вокруг шейки матки.Это действие должно высвободить гормон, называемый простагландинами. Вам не нужно попадать в больницу для этой процедуры, и ее часто делают в палате врача. Этого может быть достаточно, чтобы приступить к работе, а это значит, что вам не понадобятся другие методы.

Риски : Это простая и легкая процедура; однако это не всегда срабатывает. Это может быть немного неудобно, но не больно.

Окситоцин

Синтетическая версия гормона окситоцина вводится вам через капельницу в руку, чтобы начать схватки. Когда начинаются схватки, количество окситоцина регулируется, чтобы вы продолжали регулярные схватки до рождения ребенка. Весь этот процесс может занять несколько часов.

Риски : Окситоцин может сделать схватки более сильными, частыми и болезненными, чем при естественных родах. Скорее всего, вам понадобится обезболивающее, и за ребенком будут постоянно наблюдать. Вы не сможете много двигаться из-за капель в руке, и у вас также будет фетальный монитор вокруг вашего живота, чтобы следить за вашим ребенком.

Иногда схватки могут происходить слишком быстро, что может повлиять на частоту сердечных сокращений ребенка. Это можно контролировать, уменьшив скорость капельницы или дав вам другое лекарство.

Искусственный разрыв плодных оболочек («разбивая воду»)

Искусственный разрыв плодных оболочек (ARM) используется, когда вода не разрывается естественным путем. Врач или акушерка вводит во влагалище небольшой крюкоподобный инструмент, чтобы проделать отверстие в мембранном мешочке, в котором находятся околоплодные воды. Это увеличит давление головы ребенка на шейку матки, что может быть достаточно для начала родов. Однако многим женщинам для начала схваток также потребуется окситоцин.

Риски : ARM может быть немного неудобной, но не болезненной. Существует небольшой повышенный риск выпадения пуповины, кровотечения или инфекции.

Простагландин

Синтетическая версия гормона простагландина вводится во влагалище, чтобы смягчить шейку матки и подготовить тело к родам.Он может быть в форме геля, который можно вводить в несколько доз (обычно каждые 6-8 часов), или пессария и ленты (аналогично тампону), которые медленно высвобождают гормон в течение 12-24 часов. После введения простагландина вам нужно будет лечь и оставаться в больнице. Вам также может понадобиться ARM, если ваши воды не отошли, или окситоцин, чтобы вызвать схватки.

Простагландин часто является предпочтительным методом стимулирования родов, поскольку он наиболее близок к естественным родам.Немедленно сообщите акушерке или врачу, если у вас начнутся болезненные, регулярные схватки с интервалом 5 минут для первого ребенка или 10 минут для последующих детей. Вы также должны сообщить им, если у вас отошли воды, поскольку это оба признака начала родов.

Риски : Некоторые женщины обнаруживают, что их влагалище болит после простагландина, или они могут испытывать тошноту, рвоту или диарею. Эти побочные эффекты встречаются редко, и нет никаких доказательств того, что индукция простагландином более болезненна, чем естественные роды.

Очень редко схватки могут быть слишком сильными, что может повлиять на частоту сердечных сокращений ребенка. Это можно контролировать, дав вам другое лекарство или сняв пессарий.

Вы должны немедленно сообщить своему врачу или акушерке, если у вас начнется кровотечение или если ваш ребенок меньше двигается, поскольку это может быть признаком того, что что-то не так.

Баллонный катетер для созревания матки

Баллонный катетер для созревания шейки матки — это небольшая трубка, прикрепленная к баллону, который вставляется в шейку матки.Баллон наполняется физиологическим раствором, который обычно оказывает достаточное давление на шейку матки, чтобы он открылся. Он остается на месте до 15 часов, а затем вас снова осмотрят.

Немедленно сообщите своей акушерке или врачу, если у вас начнутся болезненные, регулярные схватки с интервалом в 5 минут для первого ребенка или с интервалом в 10 минут для последующих детей, или если у вас отошли воды, поскольку оба они являются признаком начала родов.

Вам также может потребоваться ARM или окситоцин, если вы используете баллонный катетер для созревания шейки матки.

Риски : Введение катетера может быть немного неудобным, но безболезненным.

Вам также необходимо немедленно сообщить своему врачу или акушерке, если у вас начнется кровотечение или ваш ребенок меньше двигается, потому что это может быть признаком того, что что-то не так.

Методы созревания шейки матки и индукции родов

1. Норвиц Э., Робинсон Дж., Репке Дж. Труд и родоразрешение. В: Габби С.Г., Нибил Дж. Р., Симпсон Дж. Л., ред. Акушерство: нормальная и проблемная беременность.4-е изд. Нью-Йорк: Черчилль Ливингстон, 2002: 353–94 ….

2. Американский колледж акушеров и гинекологов. Индукция родов. Бюллетень практики № 10. Вашингтон, округ Колумбия: ACOG, 1999.

3. Людмир Дж., Sehdev HM. Анатомия и физиология шейки матки. Clin Obstet Gynecol . 2000; 43: 433–9.

4. Эдвардс РК, Ричардс Д.С. Предварительная оценка шейки матки. Clin Obstet Gynecol . 2000; 43: 440–6.

5. МакФарлин Б.Л., Гибсон MH, О’Рир J, Харман П. Национальное исследование использования травяных препаратов медсестрами-акушерками для стимуляции родов. J Медсестра-акушерка . 1999; 44: 205–16.

6. Белью К. Травы и беременная женщина. Рекомендации для акушерок. J Медсестра-акушерка . 1999; 44: 231–52.

7. Adair CD. Нефармакологические подходы к затравке шейки матки и индукции родов. Clin Obstet Gynecol .2000. 43: 447–54.

8. Келли А.Дж., Кавана Дж., Томас Дж. Касторовое масло, ванна и / или клизма для затравки шейки матки и индукции родов. Кокрановская база данных Syst Rev . 2002; 2: CD003099

9. Кавана Дж., Келли Эй Джей, Томас Дж. Половой акт для созревания шейки матки и индукции родов. Кокрановская база данных Syst Rev . 2002; 2: CD003093

10. Бил М.В. Иглоукалывание и точечный массаж.Приложения к охране репродуктивного здоровья женщин. J Медсестра-акушерка . 1999; 44: 217–30.

11. Smith CA, Crowther CA. Иглоукалывание для стимуляции родов. Кокрановская база данных Syst Rev . 2002; 2: CD002962

12. Lin A, Купферминц М, Дули С.Л. Рандомизированное испытание экстраамниотического солевого раствора по сравнению с ламинарией для созревания шейки матки. Акушерский гинекол . 1995. 86 (4 часть 1): 545–9.

13.Рубен Д, Ариас Ф. Рандомизированное испытание экстраамниотической инфузии физиологического раствора плюс внутрицервикальный баллон с катетером Фолея по сравнению с вагинальным гелем простагландина E2 для созревания шейки матки и стимулирования родов у пациентов с неблагоприятными шейками матки. Акушерский гинекол . 1993; 82: 290–4.

14. Sherman DJ, Френкель Э, Панский М, Каспи Э, Буковский I, Лангер Р. Созревание шейки матки в баллоне с экстраамниотической инфузией физиологического раствора или простагландина E2: двойное слепое рандомизированное контролируемое исследование. Акушерский гинекол . 2001; 97: 375–80.

15. Buccellato CA, Стика CS, Frederiksen MC. Рандомизированное испытание мизопростола по сравнению с введением внеамниотического раствора хлорида натрия с окситоцином для индукции родов. Am J Obstet Gynecol . 2000; 182: 1039–44.

16. Гольдман Дж. Б., Wigton TR. Рандомизированное сравнение экстраамниотического солевого раствора и интрацервикального геля динопростона для созревания шейки матки. Акушерский гинекол .1999; 93: 271–4.

17. Гуинн Д.А., Goepfert AR, Кристина М, Оуэн Дж. Hauth JC. Экстраамниотический солевой раствор, ламинария или гель простагландина E (2) для индукции родов с неблагоприятной шейкой матки: рандомизированное контролируемое исследование. Акушерский гинекол . 2000; 96: 106–12.

18. Шрейер П., Шерман DJ, Ариэли С, Герман А, Каспи Э. Созревание крайне неблагоприятной шейки матки с помощью экстраамниотического солевого раствора или вагинального применения простагландина E2. Акушерский гинекол . 1989; 73: 938–42.

19. Хади Х. Созревание шейки матки и индукция родов: клинические рекомендации. Clin Obstet Gynecol . 2000; 43: 524–36.

20. Foong LC, Ваная К., Тан G, Чуа С. Подметание мембраны в сочетании с индукцией родов. Акушерский гинекол . 2000; 96: 539–42.

21. Брикер Л, Лукас М. Только амниотомия для индукции родов. Кокрановская база данных Syst Rev .2002; 2: CD002862

22. Witter FR. Препараты простагландина Е2 для прединдукционного созревания шейки матки. Clin Obstet Gynecol . 2000; 43: 469–74.

23. Ариас Ф. Фармакология окситоцина и простагландинов. Clin Obstet Gynecol . 2000. 43: 455–68.

24. Келли А.Дж., Кавана Дж., Томас Дж. Вагинальный простагландин (PGE2 и PGF2a) для индукции родов в срок. Кокрановская база данных Syst Rev .2002; 2: CD003101

25. Goldberg AB, Гринберг МБ, Дарни П.Д. Мизопростол и беременность. N Engl J Med . 2001; 344: 38–47.

26. Американский колледж акушеров и гинекологов. Индукция родов мизопростолом. Мнение комитета ACOG 228. Вашингтон, округ Колумбия: ACOG, 1999: 2.

27. Lydon-Rochelle M, Холт В.Л., Истерлинг TR, Мартин Д.П. Риск разрыва матки во время родов у женщин, перенесших кесарево сечение. N Engl J Med . 2001; 345: 3–8.

28. Sanchez-Ramos L, Годье FL, Кауниц AM. Созревание шейки матки и индукция родов после предыдущего кесарева сечения. Clin Obstet Gynecol . 2000; 43: 513–23.

29. Венгалил С.Р., Гуинн Д.А., Олаби Н.Ф., Бурд Л.И., Оуэн Дж. Рандомизированное испытание мизопростола и экстраамниотического солевого раствора для созревания шейки матки и индукции родов. Акушерский гинекол .1998. 91 (5 часть 1): 774–9.

30. Hofmeyr GJ, Гюльмезоглу AM. Вагинальный мизопростол для созревания шейки матки и индукции родов. Кокрановская база данных Syst Rev . 2002; 2: CD000941

31. Sanchez-Ramos L, Кауниц AM. Мизопростол для созревания шейки матки и индукции родов: систематический обзор литературы. Clin Obstet Gynecol . 2000. 43: 475–88.

32. Neilson JP. Мифепристон для индукции родов. Кокрановская база данных Syst Rev . 2002; 2: CD002865

33. Келли А.Дж., Кавана Дж., Томас Дж. Релаксин для созревания шейки матки и индукции родов. Кокрановская база данных Syst Rev . 2002; 2: CD003103

34. Zeeman GG, Хан-Дауд Ф.С., Дауд М.Ю. Окситоцин и его рецепторы во время беременности и родов: современные концепции и клиническое значение. Акушерский гинекол . 1997. 89 (5 pt 2): 873–83.

35.Стаббс TM. Окситоцин для стимуляции родов .. Clin Obstet Gynecol . 2000; 43: 489–94.

Дедуктивные рассуждения в сравнении с индуктивными рассуждениями

В научном процессе дедуктивное рассуждение используется для достижения логического истинного заключения. Также используется другой тип рассуждений, индуктивный. Часто люди путают дедуктивное рассуждение с индуктивным, и наоборот. Важно знать значение каждого типа рассуждений, чтобы можно было определить правильную логику.

Дедуктивное рассуждение

Дедуктивное рассуждение — это основная форма действительного рассуждения. Согласно Калифорнийскому государственному университету, дедуктивное рассуждение или дедукция начинается с общего утверждения или гипотезы и исследует возможности для достижения конкретного логического вывода. Научный метод использует дедукцию для проверки гипотез и теорий. «В дедуктивном выводе мы придерживаемся теории и на ее основе делаем предсказание ее последствий. То есть мы предсказываем, какими должны быть наблюдения, если теория верна.Мы переходим от общего — теории — к частному — наблюдениям «, — сказала д-р Сильвия Вассертхайль-Смоллер, исследователь и почетный профессор Медицинского колледжа Альберта Эйнштейна.

Дедуктивное рассуждение обычно следует за шагами. посылка, затем вторая посылка и, наконец, умозаключение. Распространенной формой дедуктивного рассуждения является силлогизм, в котором два утверждения — основная посылка и второстепенная посылка — достигают логического заключения. Например, посылка «Каждый А есть Б. «может последовать другая посылка:» Это C есть A.«Эти утверждения привели бы к заключению:« Это C есть B. »Силлогизмы считаются хорошим способом проверки дедуктивного мышления, чтобы убедиться, что аргумент верен.

Например,« Все люди смертны. Гарольд — мужчина. Следовательно, Гарольд смертен ». Чтобы дедуктивное рассуждение было правильным, гипотеза должна быть верной. Предполагается, что посылки« Все люди смертны »и« Гарольд — человек »верны. Следовательно, вывод логичен и В дедуктивных рассуждениях, если что-то верно для класса вещей в целом, это также верно для всех членов этого класса.

Согласно Калифорнийскому государственному университету, выводы дедуктивного вывода верны при условии, что посылки верны. Можно прийти к логическому выводу, даже если обобщение неверно. Если обобщение неверно, вывод может быть логичным, но может и неверным. Например, аргумент: «Все лысые — деды. Гарольд лысый. Следовательно, Гарольд — дедушка» логически верен, но неверен, поскольку исходное утверждение ложно.

Индуктивные рассуждения

Индуктивные рассуждения противоположны дедуктивным рассуждениям.Индуктивное рассуждение делает широкие обобщения на основе конкретных наблюдений. В основном данные есть, потом на основании данных делаются выводы. Согласно Университету штата Юта, это называется индуктивной логикой.

«В индуктивном выводе мы переходим от частного к общему. Мы делаем много наблюдений, различаем закономерности, делаем обобщение и делаем вывод об объяснении или теории», — сказал Вассертхайль-Смоллер Live Science. «В науке существует постоянное взаимодействие между индуктивным выводом (основанным на наблюдениях) и дедуктивным выводом (основанным на теории), пока мы не приближаемся все ближе и ближе к« истине », к которой мы можем только приблизиться, но не установить с полной уверенностью.«

Пример индуктивной логики:« Монета, которую я вытащил из сумки, — это пенни. Эта монета — пенни. Третья монета из мешка — пенни. Следовательно, все монеты в сумке — пенни ».

Даже если все предпосылки в утверждении верны, индуктивное рассуждение позволяет сделать вывод ложным. Вот пример:« Гарольд — дедушка. Гарольд лысый. Следовательно, все деды лысые ». Вывод не следует логически из утверждений.

Индуктивное рассуждение имеет свое место в научном методе.Ученые используют его для создания гипотез и теорий. Дедуктивное рассуждение позволяет им применять теории к конкретным ситуациям.

Абдуктивное рассуждение

Другая форма научного рассуждения, которая не вписывается в индуктивное или дедуктивное рассуждение, — это абдуктивное рассуждение. Согласно Батт-колледжу, абдуктивное рассуждение обычно начинается с неполного набора наблюдений и переходит к наиболее вероятному возможному объяснению группы наблюдений. Он основан на создании и проверке гипотез с использованием наилучшей доступной информации.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *