Рациональный и иррациональный виды мышления — Блог Викиум

Рациональный и иррациональный виды мышления — это две противоположности. Первый вид восприятия позволяет рационально решать различные задачи, а второй — находить нестандартные пути в самых разных ситуациях.

Рациональное мышление

Рациональный тип мышления позволяет четко видеть факты, находить правильные и эффективные пути решения различных задач. Человек, обладающий таким мышлением, видит вещи в их истинном свете и может их адекватно анализировать.

Обычно рациональный тип мышления связывают с людьми, которые работают в различных областях и пользуются этими способностями для достижения определенных целей. Но на самом деле рациональный тип мышления бывает полезен и в повседневной жизни. Он помогает обычным людям решать насущные проблемы и находить правильные выходы из разных ситуаций.

Личности с рациональным мышлением обладают рядом признаков:

• Рационально оценивают данность;
• Понимают, какие цели им по плечу;
• Воспринимают критические замечания и учитывают их;
• Обладают такими качествами как прагматизм и расчетливость.

Этот тип мышления позволяет быстро, ввиду того, что каждый шаг их просчитан принимать правильные решения, видеть все достоинства и недостатки той или иной ситуации. Люди, обладающие рациональным мышлением, часто достаточно успешны.

Что такое иррациональное мышление

Те, кто обладает рациональным типом мышления, как правило, не обладает никакими особенными способностями к воспроизведению образов, к фантазиям, имеют определенные ограничения в этих аспектах.

В то же время, те, кто обладает мышлением иррациональным, могут при принятии решений руководствоваться чувствами, впечатлениями, просто душевным состоянием.

Лучше всего иррациональное мышление демонстрируют дети. Именно они не ограничены никакими рамками, говорят то, что думают, не размышляя о последствиях. Обладают способностью фантазировать и представлять даже самые немыслимые ситуации. В детском сознании отсутствуют такие понятия как рассудительность и задумчивость относительно собственных поступков. Именно поэтому они могут принимать иррациональные решения.

Множество знаменитых людей имели именно иррациональный тип мышления. Это были художники, писатели, драматурги и другие. Многие из них в последствие стали знаменитыми, и все благодаря тому, что использовали именно иррациональный тип мышления.

По сути, рациональный и иррациональный виды мышления являются двумя сторонами одной медали. Если разобраться, то человеку необходимы навыки в обеих областях, тогда как часто люди выбирают только один тип, который кажется наиболее верным.

Если трезво оценивать все эти факторы, то нужно признать, что рациональное и иррациональное мышление идут рука об руку, никак не мешая друг другу, но, наоборот, дополняя.

Как правило, успешные люди в одинаковой мере обладают обоими типами мышления, успешно их используют и с помощью их решают огромное количество сложных  задач.

Формирование того или иного типа мышления происходит на протяжении всей жизни, обладать им может как взрослый, так и ребенок. В то же время, мотивировать на приобретение определенных навыков может родитель ребенка или наоборот.

Человек разумный выбирает комбинацию обоих типов мышления, при этом форма их может очень сильно различаться, однако на сегодняшний день существуют специальные тесты, которые способны показать принадлежность личности к тому или иному типу мышления.

Подытоживая, можно сказать, что каждый, кто хочет стать по-настоящему успешным, должен стремится к тому, чтобы развивать и иррациональное, и рациональное мышление. Научиться думать рационально, грамотно выстраивать аргументацию и, наконец, овладеть всеми преимуществами логики можно с помощью курса «Мышление Шерлока». Занимательные головоломки, простое и понятное объяснение основных логических законов — все это поможет стать не просто более рациональным, но и обрести такие качества, которым бы позавидовал сам Шерлок Холмс!

Рациональное и иррациональное с позиции философии обыденного сознания Текст научной статьи по специальности «Философия, этика, религиоведение»

RATIONAL AND IRRATIONAL FROM THE VIEWPOINT OF ORDINARY CONSCIOUSNESS

Baranov Stanislav Trofimovich, DSc of Philosophy, Professor, Department of Social Philosophy and Ethnology, North-Caucasus Federal University, Stavropol

Bokachev Ivan Afanasievich, DSc of Philosophy, Professor, Leading Researcher, institute for Advanced Training of Scientific and Pedagogical Personnel, North-Caucasus Federal University, Stavropol

Neznamova irina Ivanovna, PhD of Philosophy, head of Department, Stavropol branch of Moscow Humanitarian and Economic University, Stavropol

The article presents a scientific analysis of rational and irrational as philosophical categories, if rational is a consciousness phenomenon and is used as universal way to study the World and human beings in it, then irrational defines impact of concealed forces which are currently hypothetical, unexplored and unexplained but nevertheless remain valuable for learning and developing scientific knowledge.

The article emphasizes similarities and differences as well as defines place and importance of rational and irrational in scientific and artistic practices.

Keywords: rational; irrational; concealed forces; intuition, ordinary consciousness; images and symbols as expression of reality; abstraction on art; avant-garde in art.

РАЦИОНАЛЬНОЕ И ИРРАЦИОНАЛЬНОЕ С ПОЗИЦИИ ФИЛОСОФИИ ОБЫДЕННОГО СОЗНАНИЯ

В качестве объекта научного анализа, содержащегося в статье, — представлены рациональное и иррациональное как философские категории. Если рациональное рассматривается как феномен сознания, как универсальный способ познания Мира и человека в нем, то иррациональное обозначает действие скрытых сил, которые гипотетичны, пока непознаны и необъяснимы, но, тем не менее, важны для познания, для развития науки. Акцент в статье сделан на вопросах единства и различия, на определении места и роли рационального и иррационального в научной и художественной деятельности.

Ключевые слова: рациональное; иррациональное; скрытые силы; интуиция; обыденное сознание; образы и символы как выражение действительности; абстракция в искусстве; авангардизм в искусстве.

УДК 130.2 ВАК РФ 09.00.13

© Баранов С. Т., 2018 © Бокачев И. А., 2018 © Незнамова ИМ, 2018

Слово «рациональное» обозначает объективно существующий феномен в сознании человека, характеризующий его стремление познавать мир вокруг себя и самого себя в этом мире посредством логических форм. Известно, что в структуре сознания все его нравственные, эстетические и другие элементы имеют свой антипод. Например, мужество — трусость; честность — хитрость; любовь к людям — эгоизм, жестокость; бескорыстие — жадность, корыстолюбие; решительность — малодушие; и т. п. Противоположности, составляющие пары, всегда находятся вместе в сознании индивида, но по-разному влияют на характер, а также на его поведение. Этот факт безусловный и никем не оспариваемый.

Сопутствующим спутником рационального является иррациональное. Иррациональное — не иллюзия, не фантом, а реально существующее в нашем повседневном сознании, сложнейшее явление, трудно поддающееся однозначным толкованиям и кратким определениям. Иррациональное не только носитель эмоций, но и определенных информаций. Парадокс заключается в том, что непосредственный носитель информации, обозначаемый словом иррациональное, пока есть недоступное для средств научного познания. Поэтому он гипотетичен, тем не менее, важен для познания, необходим для движения науки. Гениальный русский мыслитель Елена Петровна Блават-ская утверждала, что не существует ничего сверхъестественного, а есть лишь непознанное, необъяснимое в настоящее время. Это утверждение имеет прямое отношение к характеристике иррационального. Мир вечен и бесконечен, а значит, бесконечен и процесс познания, а, следовательно, всегда будет иррациональное, как обозначение скрытых сил, действие которых в бытии человека уже обо-

БАРАНОВ Станислав Трофимович, доктор философских наук, профессор, кафедра Социальной философии и этнологии, СевероКавказский федеральный университет, Ставрополь

БОКА ЧЕВ Иван Афанасьевич, доктор философских наук, профессор, ведущий научный сотрудник Института повышения квалификации научно-педагогических кадров, Северо-Кавказский федеральный университет, Ставрополь

НЕЗНАМОВА Ирина Ивановна, кандидат философских наук, заведующий отделением, Ставропольский филиал Московского гуманитарно-экономического университета, Ставрополь

значилось. Иррациональное — важнейший психологический фактор, имеющий огромное значение для формирования рационального как способа познания среды и адаптации к ней.

Иногда к иррациональному относят явления, называемые, алогичными, как бы находящимися за пределами действия универсальных принципов и законов. В данном случае закономерности рассматриваются в узком масштабе, игнорируя двойственность, как это наблюдается в философии постмодернизма. У постмодернистов особая неприязнь к диалектике, как универсальному свойству развития. Ими отвергаются все бинарные половозрастные, познавательные, нравственные, эстетические, классовые и другие позиции. Отрицается истина как единство абсолютного и относительного, объективного и субъективного, абстрактного и конкретного. Рациональному философы-постмодернисты противопоставляют иррациональное, научному знанию -обыденное, логическому — эмоциональное. Еще в свое время Г.В.Ф. Гегель отмечал, что противопоставление научному знанию непосредственное знание «весьма скудное и совершенно бессодержательное определение»[1 ,с. 414].

Обособление интеллектуального и непосредственного, эмоционального своими корнями восходит к древнегреческой философии. Эта идея находит отражение в логическом учении Аристотеля. Для античного философа принципы и законы, сформулированные им в «Логике» абсолютны и независимы от психологических феноменов. Аристотелевское представление о принципиальном различии интеллектуальной и эмоциональной сфер человеческого сознания просуществовало вплоть до XX века.

Все это дает основание полагать: понятие иррационального — широкое понятие, его нельзя свести к чисто субъективному, к «деталям, отсутствующих в самой реальности и создаваемых воображением» [2, с. 43]. Иррационализм — это единство объективного и субъективного, специфику проявления которого следует рассматривать через связь и взаимодействие, так называемого, теоретического и обыденного сознания. Теоретическое и обыденное — это не уровни представлений, знаний, они сферы, способы бытия человека, наложенные друг на друга.

В советской марксистско-ленинской философии не исключалась роль субъективного, например, в познании, диалектике объекта и субъекта, объективного и субъективного. Этим проблемам было посвящено большое количество научных исследований. Но в понимании

субъективного отсутствовало иррациональное, как важнейший элемент сознания, играющее весьма существенную роль в познавательном процессе. Рациональное и иррациональное рассматривались обособленно друг от друга, считалось, что рациональность — разумность, а иррациональное — неразумность. Утверждалось, что рациональность и иррациональность — это не те противоположности, между которыми существует диалектическая взаимосвязь, они абсолютно исключают друг друга. В эпоху классической философии рациональность, разумность выдвигались на первое место, признавались основной характеристикой мира. Например, в философской концепции Гегеля демиургом всего существующего был признан Мировой Разум. Однако в постклассической философии отношение к рационализму и иррационализму резко меняется — приоритет переходит от рационализма к иррационализму. И это не случайно. Говоря словами С.Л. Франка, наступила эпоха «…глубочайшего безверия, скепсиса, духовной разочарованности и охлажденности» [3, с. 17].

В XIX веке К. Маркс (1818-1883) создаётуче-ние о коммунизме, обществе, которое можно построить посредством совершения социалистической революции и установления диктатуры пролетариата. Марксистская теория спровоцировала Октябрьскую 1917 г. революцию, которая переросла в Гражданскую войну. В результате основательно были нарушены все сферы жизнедеятельности многочисленных народов национальных областей, входивших в состав России.

В XX веке относительно спокойное социальное развитие сменяется трагическими событиями: происходят две мировые войны, в результате которых пострадало и погибло огромное количество людей.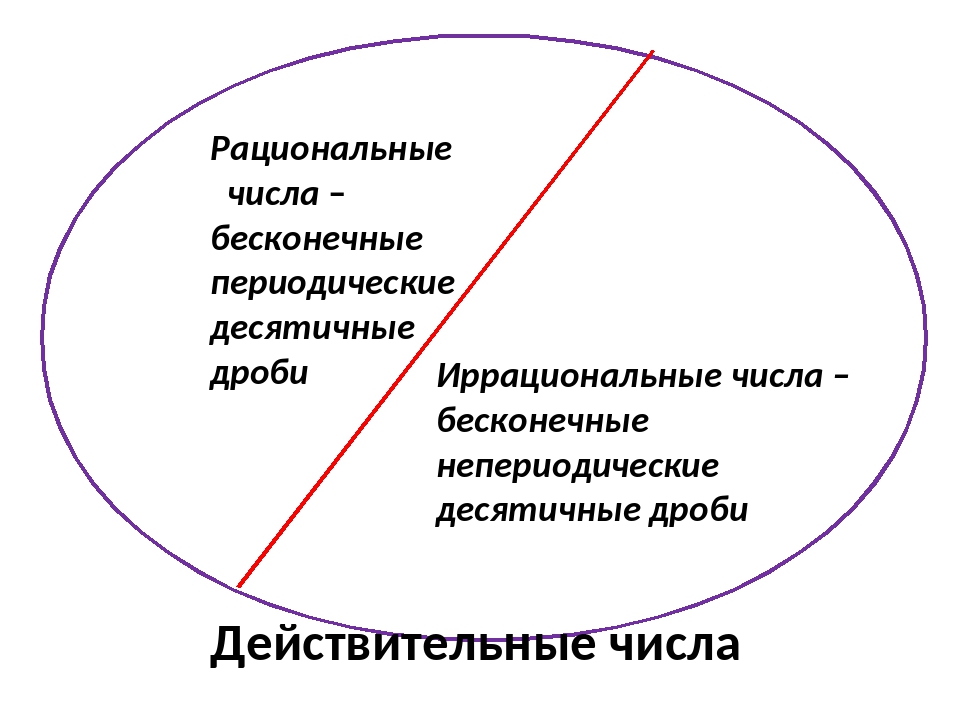 Во второй половине этого же века возникают глобальные проблемы, угрожающие существованию всего человечества. С особой остротой заявляет о себе экологический кризис. Причины этого кризиса просты и очевидны: прежде всего, это эгоистическое отношение человеческого рода к природе, потребительски-захватническое использование ее ресурсов.

Нестабильный, взрывоопасный мир способствует формированию и распространению лживой, лицемерной, антигуманной, бездуховной идеологии, энергично распространяемой СМИ по всем странам и континентам. Подобная идеология не только не стабилизирует, а, наоборот, «раскачивает» мир, толкая его все ближе и ближе к пропасти. Да, альтернатив-

ное мировоззрение существует, но оно подавляется всеми имеющимися техническими, информационными средствами, которыми владеет, которые контролирует и направляет мировая финансовая элита.

Новая историческая эпоха выражается также в таких философских дискурсах, как экзистенциализм, постструктурализм, трансгуманизм (элитный), «золотой миллиард» и т. п. Эти учения и взгляды знаменуют отказ от признания разумных оснований социума, на первый план выдвигается идея иррационального характера действительности. Известный представитель постмодернизма Ж. Деррида объявил, что разум «ужасный, коварный Господин и призвал вступить в жестокую борьбу против него. Он сформулировал стратегию деконструкций, которая доказывает, что истинное не является подлинно истинным, закон не отличается от произвола»[4]. С обострением кризисных симптомов развития общества в XX и XXI веках иррационалистические умонастроения получают весьма широкое распространение. Особое внимание при этом уделяется произведениям Ф. Г. Якоби, Ф. В. И. Шеллинга, А. Шопенгауэра, С. Кьеркегора, в которых легко просматриваются иррационалистические тенденции.

Иррациональное стало ассоциироваться, во-первых, с якобы существующими алогичными свойствами человеческого сознания; во-вторых, внетеоретическим знанием, основанным на интуиции и воображении. Многие ученые самых разных направлений были склонны утверждать, что одним разумом познать действительность невозможно, существуют скрытые силы, которые нельзя выразить в понятиях.

Л. Н. Толстой, пытаясь понять исторический процесс и роль личности в нем, пришел к выводу: «Один, только один есть у нас непогрешимый руководитель, всемирный Дух, проникающий нас всех вместе и каждого, как единицу, влагающий в каждого стремления к тому, что должно»[5, с.48]. Говоря о роли Наполеона в сражениях в России, писатель сравнивал французского императора с ребенком, «который держась за тесемки, привязанные внутри кареты, воображает, что он правит»[6, с. 199].

Современный рационализм до сих пор использует многие идеи гуссерлевского наследия. Немецкий философ Э. Гуссерль поиски скрытых, таинственных сил перенес с высоких небес в глубины человеческого сознания. Ученик Гуссерля М. Хайдеггер последовательно и органично применял методы и установки уче-

ния Гуссерля для критики научного познания, для обоснования своего учения иррационального психологизма. Главной задачей своей философии (феноменологии) Гуссерль считал поиски несомненных основ познания. Истина, по Гуссерлю, относится к сфере идеального, которая не имеет «человеческого», «временного» характера и которая вообще не обладает статусом существования. Это мир «чистых сущностей». Мир научныхтеорий, научного познания Гуссерль ставит в зависимость от «донаучного», «вненаучного» сознания, состоящего из суммы непосредственных «очевидностей». Он называет «жизненным миром» сферу «первоначальных очевидностей», нерефлективного «верования». Сфера дорефлексивных фундаментальных очевидностей — это главная сфера обыденного сознания. По мнению Гуссерля, причиной глубокого кризиса европейской рациональности стала утрата связи «чистых» понятий и обыденного сознания в ходе исторического развития.

У представителей «философии жизни» В. Диль-тея, О. Шпенглера, Ф. Ницше, А. Бергсона абсолютные основания бытия мира и человеческой деятельности не имеют рационального характера, они иррациональны. Бергсон утверждает, что в сознании человека множество новых пластов, неизвестных чисто рационалистическому объяснению, неподвластных социальным регуляциям и ограничениям. Глубинными пластами сознания человека объявляются бессознательное и интуиция, которые становятся главными понятиями в философской концепции Бергсона. У Бергсона интуиция представлена и как познание, и как миросозерцание, и как способ ориентации человека в мире, в сложных и изменчивых обстоятельствах общественной и индивидуальной жизни.

Большая часть концепций мировой философии, начиная с античных времен и до XXI века, в основе своей иррационалистична. По большому счету главным философским вопросом было признание существования философского разума. Эту мысль неоднократно подтверждал Гегель, заявляя, что философия своими методами и способами постоянно доказывала бытие Бога. Зигмунд Фрейд перенес внимание философов на ту часть сознания, которую назвал сферой неуправляемых инстинктов, доказывая, что сознательное — маленький островок в океане бессознательного. Фрейдовская идея была подхвачена исследователями разных философских, социологических, культурологических направлений и продолжает развиваться до сих пор во множестве

вариантов. Человек живет в мире, где познанное переплетается с непознанным. Познанное — это знакомый мир, который позволяет человеку жить в нем, опираясь на здравый смысл и инстинкты самосохранения. Непознанное -это невидимый, незнакомый мир, к которому человек относится настороженно, но, тем не менее, пытливо направляясь навстречу к нему. Блаватская верно заметила, что сверхъестественное — то, что называют иррациональным в сфере еще непознанного. В идее Бога рациональное сосуществует с так называемым иррациональным, иррациональное здесь — это особая форма проявления рационального.

Основными формами познавательной деятельности являются научная и художественная, в которых содержатся и рациональное, и иррациональное. Некоторые искусствоведы большое внимание уделяют анализу иррационального в процессах художественной деятельности. Они считают, что в творчестве решающее значение имеет иррациональное. Однако для убедительности данного тезиса им не хватает самого главного — вразумительной характеристики иррационального, они вынуждены ограничиваться лишь общими, смутными характеристиками данного феномена. Например, утверждается наличие в сознании художников иррационального мышления, недоступного ни для разума, ни для рассудка. Иррациональное мышление самостоятельно, независимо от понятийного научного мышления, а также и от интуиции. Б. Раушенбах считает, что не меньшее, а может быть большее, значение для научного и художественного творчества имеет иррациональное мышление [7], которое открывает новые области творческого импульса, не поддающееся рациональному объяснению.

В XXI веке данная концепция получила широкое распространение в отечественной литературе, особенно в литературе искусствоведческого и культурологического толка. Этот взгляд заслуживает быть названным — шаманским. Творческий художественный процесс, в ходе которого создаются произведения, это и есть движение мысли от иррационализма к рационализму, материальному миру. Считается, что только с позиций иррационализма можно понять и признать выдающимся художественным достижением произведения Малевича и других представителей абстракционизма и авангардизма.

В данном случае иррационализм представляют как некую самостоятельную субстанцию, находящуюся в подсознании и определяющую

содержание и характер творческой деятельности художника или музыканта. Иррациональное мышление — скрытая, неведомая сила, которую лучше назвать духом, связанным с трансцендентальным всезнающим миром. Дух — посредник между трансцендентальным миром и человеком, получающим направление своей деятельности вначале на бессознательном уровне, затем происходит материализация полученной информации в слове, на полотне, или в музыке и т. д.

Усиление внимания к проблеме иррационального в жизнедеятельности людей в XX, XXI веках обусловлено следующими мотивами. Во-первых, именно в этот период была потеряна безусловная вера в науку, как безграничное средство решения всех социальных проблем. Во-вторых, многие ученые не считают рационализм единственным способом познания. Кроме того, некоторые исследователи, особенно абстракционизма и авангардизма в своей художественной деятельности, анализ этих направлений строят на иррационализме, утверждая, что они представляют новое иррациональное мышление. По их мнению, иррациональная мысль спасает искусство от материализма и рационализма, которые якобы обезличивают искусство. В иррациональной мысли, в её чувственном выражении не существует реального времени и точных материальных объектов. Это первичный мир явлений, а мир объективных предметов реальностей есть вторичный мир. Таким философским способом апологеты авантюризма в искусстве пытаются защитить это направление и убедить обывателей, не признающих эстетическую ценность этого скандального искусства, что они не доросли до понимания настоящего художественного творения.

Признание приоритета художественного творчества над научным отмечалось и в недалеком прошлом. Например, те же представители «философии жизни» утверждали, что процесс жизни неподвластен аналитической деятельности разума. Научному познанию противопоставляются неинтеллектуальные, интуитивные, образно-символические способы познания жизненной реальности, которые, по их мнению, в основе своей иррациональны. Произведения искусства, живопись, поэзия, музыка объявляются наиболее адекватными средствами и способами постижения и выражения жизни. Некоторые современные исследователи рационализма и иррационализма говорят о принципиальной невозможности логического анализа эстетического со-

держания. Они утверждают, что «…познавательное содержание, заключенное в науке и искусстве неодинаково и, разумеется, художественная картина мира непереводима на язык научных понятий» [8, с. 175]. В основе приведенных рассуждений лежит гносеологическая традиция разграничения искусства и науки как образного и понятийного отражения действительности.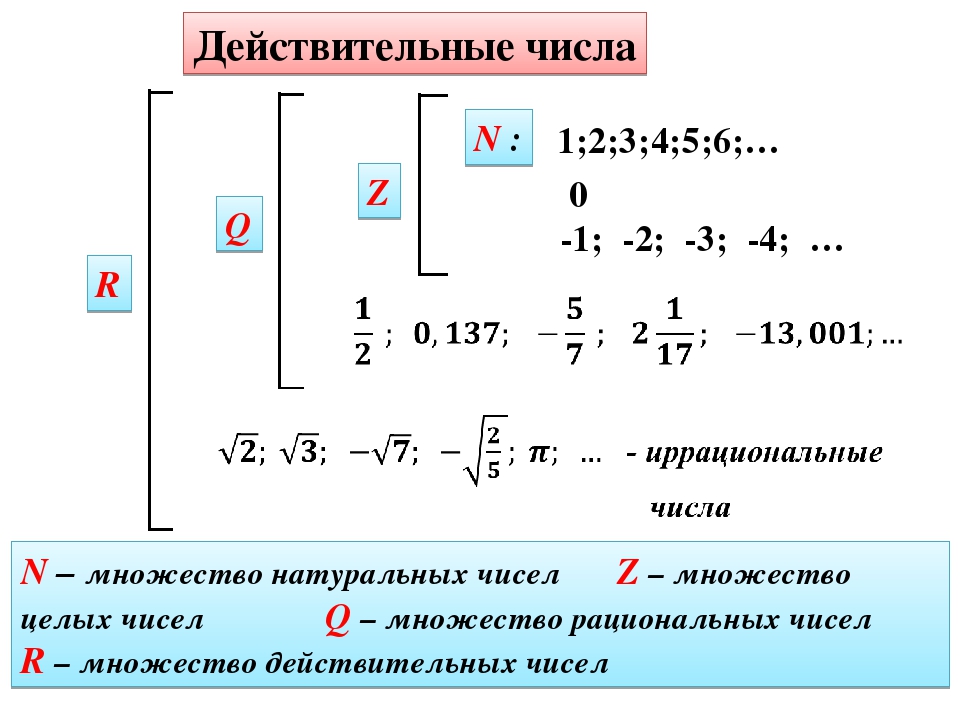

Примечания:

1. Гегель Г.В.Ф. Сочинения. Т.2 / Г.В.Ф. Гегель. — М.:

Политиздат, 1932. — 186 с.

2. Гусев С. С. Рациональность: истоки и эволюция.

// Философские науки. — 2015. — № 5. — 438 с.

3. Франк С.Л. Духовные основы общества. — М. : Республика, 1992. — 511 с.

4. Деррида Ж. От экономии ограниченной к всеобщей экономики / Ж. Деррида // http:www.philosophy.ru/Mbrary/derrida/ ekonom.html 21 января 2017.

5. Толстой Л.Н. Из записок князя Д.Нехлюдова (Люцерн). Собр.соч. в 20 тт. — М. : Государственное издательство художественной литературы,1960. Т.З. — 255 с.

6. Толстой Л. Н. Собрание сочинений. — М. : Правда, 1948. — Т.2. — 289 с.

7. См.: Раушенбах Б.В. Пространственное построение в живописи. — М., 1980. — 288 с.

8. Зись А. Я. Конфронтация в эстетике. — М.: Искусство, 1980. — 239 с.

SYMBOLIC OF DEATH IN THE SPRING FOLKLORE OF GREBENSKY COSSACKS

Grigoryev Anatoly Fedorovich, DSc of Cultural studies, PhD of Pedagogical science, Professor, Honored Artist of the ChR, Department of Theory and Methods of Music Education, Stavropol State Pedagogical State Institute, Stavropol

Specific lifestyle Greben Cossacks related to military service and significantly influenced their songwriting. Greben Cossacks folk songs full of pictures of the development of the North-Eastern Caucasus and reflects the history of the protection of the southern borders of Russia. A significant part of folk songs, with various genres, dedicated to the themes of the internal life of the Village, the military campaigns, life and death of a Cossack, often far away from their native village. Category death through all songs of the Cossacks, reflect the widest palette of life twists and turns, inevitably couching them in emotionally-shaped.

Keywords: symbols of death; folk songs Greben Cossacks; Musica Poetica; sound images, military themes; metaphor, military campaigns; service.

СИМВОЛИКА СМЕРТИ В ПЕСЕННОМ ФОЛЬКЛОРЕ УДК 128

ГРЕБЕНСКИХ КАЗАКОВ ВАКРФ09.00.13

Специфический образ жизни гребенских казаков, связанный с воинской служ- © Григорьев А.Ф., 2018 бой, ощутимо повлиял и на их песенное творчество. Песенный фольклор гре-бенского казачества насыщен картинами освоения Северо-Восточного Кавказа и отражает историю защиты южных рубежей России. Значительная часть песенного фольклора, причем различных по жанру, посвящена темам внутреннего станичного быта, военных походов, службы и смерти казака, чаще всего вдали от родной станицы. Категория смерти проходит через все песенное творчество казаков, отражает широчайшую палитру жизненных перипетий, неизбежно облекая их в эмоционально-образные формы. Ключевые слова: символика смерти; песенный фольклор гребенских казаков; музыкальная поэтика; звукообразы, военная тематика; метафора, военные походы; служба.

Символика смерти представляет один из малоизученных фило-софско-культурологических аспектов. В песенном фольклоре гребенских казаков она представляет феноменальную область традиционного песенного творчества и практически никем не исследованную. Впервые данная проблематика исследовалась автором статьи в монографии «Историософия гребенских казаков в этнической картине мира».

Одна из центральных тем в песенном фольклоре гребенских казаков — воинская служба, которая, сопровождая всю жизнь казаков со всеми тяготами и перипетиями, именовалась зачастую в песне матушкой. Анализ поэтического содержания песенного фольклора позволяет еще раз утвердиться в истинности выражения Дж. Вико о

ГРИГОРЬЕВ Анатолий Федорович, доктор культурологии, кандидат педагогических наук, профессор, заслуженный деятель искусств ЧР, кафедра Теории и методики музыкального образования, Ставропольский государственный педагогический государственный институт, Ставрополь grig. 26rus@gmaii com

Урок 5. Иррациональное мышление

Предыдущий урок мы закончили на утверждении, что одной из самых серьезных преград на пути развития критического мышления является иррациональное мышление. Но что же это такое? Почему оно свойственно многим людям? Какое влияние оно оказывает на жизнь и деятельность человека? Как от него избавиться и нужно ли это делать? На эти и некоторые другие вопросы мы ответим в пятом уроке.

Содержание:

Иррациональное и его характеристика

Если попытаться объяснить понятие «иррациональное» с позиции философии, то охарактеризовать его можно как определенное начало человеческой натуры, противоположное свойству рационально, т.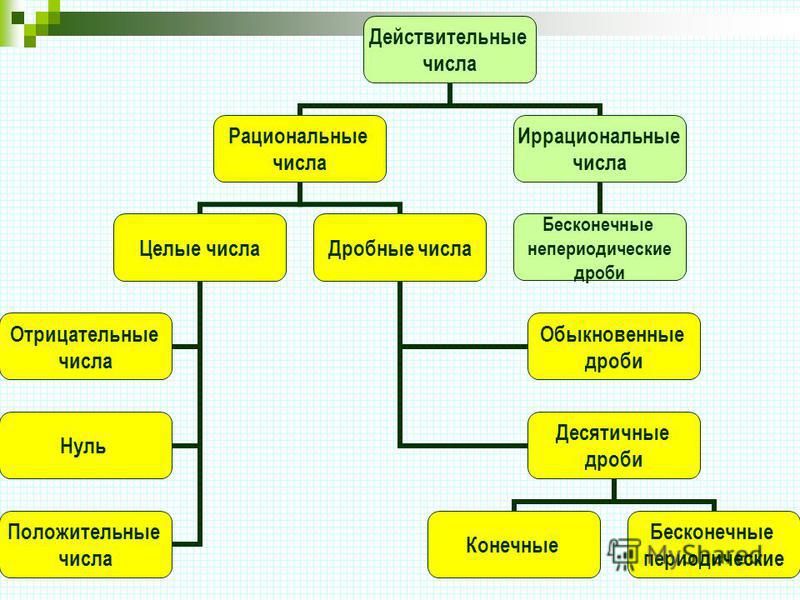 е. разумно постигать этот мир. Иррациональное допускает, что существуют такие области мировоззрения, которые разум не в состоянии понять, но все же они приемлемы благодаря вере, чувствам, интуиции. Таким образом, иррациональное – это одна из характеристик особого характера действительности. На протяжении многих лет вопросы иррационального изучались такими известными философами, как Бергсон, Дельтой, Ницше, Шопенгауэр и многие другие.

Мыслить иррационально могут позволить себе, так скажем, «свободные» личности, не задумывающиеся о последствиях. Действовать так значит допускать, что действительность не всегда может быть понята с помощью научных методов. Исходя из воззрений сторонников иррационального мышления, реальность со всеми ее компонентами и производными, например, жизнью и психологическими процессами, неподвластна общепринятым законам.

Безусловно, такая позиция имеет место быть, но в случае с критическим мышлением она совершенно не подходит. Иррациональные люди стремятся познать законы бытия, нарушая все общепринятые законы, а люди рациональные, напротив, мыслят критически, не доверяя тому, что нельзя проверить, опираясь только на достоверные и подтвержденные факты. И, беря это в расчет, мы должны сказать, что даже в том случае, если иррациональное вам свойственно, при желании развивать умение мыслить критически вы хотя бы на время должны отбросить все, что может ему противоречить.

Что же именно отбрасывать? Давай постараемся уточнить этот момент, ведь иррациональные мысли могут быть разных типов.

Типология иррациональных мыслей и их влияние

Иррациональные мысли – это мысли, мешающие объективному и адекватному восприятию окружающей действительности, а с позиции поведенческой психологии – даже служащие причиной появления необоснованной тревоги.

Всего можно выделить три категории иррационального мышления и соответствующие им типы мыслей:

• Преувеличение. Сюда относятся мысли типа: «Она заметила, что я был не уверен в себе», «Они точно подумали, что со мной что-то не так», «Он видит меня насквозь» и т.д.
• Сверхобобщение. Сюда относятся мысли типа: «Если я струсил тогда, значит, струшу и сейчас», «Он со всеми так общается – и меня не обойдет стороной», «Этот экзамен не сдал никто – у меня нет шансов» и т. д.
• Чтение мыслей. Сюда относятся мысли типа: «Она считает, что я злой и конфликтный», «Я знаю, что ты обо мне думаешь», «Он понял, что я плохо о нем подумал» и т.д.

Есть и другие типы подобных мыслей, но в той или иной степени они будут относиться к одной из категорий иррационального хода мыслей. Самая же большая их опасность в том, что они продуцируют запуск катастрофического мышления: человек с головой погружается в безосновательные волнения и панику, а его способность принимать решения и действовать полностью парализуется. Ни о каком критическом мышлении здесь не может быть и речи.

Злободневные наглядные примеры иррационального мышления вы можете найти в книгах, посвященных работе с ним. Вот несколько вариантов:

Здесь же будет логично поговорить немного и о том, как влияет иррациональное мышление на то, что делает человек.

Как уже стало ясно, иррационально значит нелогично, ненаучно и без какой-либо критики. Иррациональные действия направлены на получение результата, однако сами поступки никак заранее не обдумываются и не оцениваются. Здесь нет осмысленных заблаговременно возможных вариантов развития хода событий, разрешения вопросов или решений задач.

Все это, как правило, имеет самую прямую связь со спонтанным проявлением чувств и эмоциями, раздражающими или успокаивающими мысли. Иррациональные личности могут наблюдать проявления действительности вне пределов их логических объяснений, а также склонны верить неподтвержденным фактам просто потому, что они довлеют над другими. Такие люди пренебрегают использованием так называемых жизненных инструкций, т.е. продуманных стратегий поведения и алгоритмов действий. Основой такого поведения в большинстве случаев служит вера человека в положительный исход, даже если он совершенно не понимает практические основы и причины успеха в случае его достижения. Чаще всего успех объясняется удачей или благосклонностью судьбы.

Но с практической и тем более с критической позиции позволить себе так себя вести может либо очень духовный человек, либо ребенок. К тому же, размышляя или делая выводы, эффективно руководствоваться правилом сохранения энергии, и мыслить иррационально, просто опираясь на шаблоны и первую поступившую информацию, менее затратно с точки зрения расхода времени и сил. Но если основанные на воспитании или полученном опыте знания иррациональны, ничего хорошего из этого не выйдет.

Вот лишь небольшой перечень факторов, препятствующих эффективному мышлению и правильным действиям – иррациональное мышление:

• Спонтанно и безосновательно
• Уводит человека в сторону от правильных мыслей
• Может помешать человеку в процессе ежедневной деятельности
• Снижает эффективность в профессиональной и других сферах
• Часто активизируется тогда, когда это не нужно
• Служит причиной раздражительности, депрессии и тревоги
• Нарушает адаптацию к внешнему миру
• Не отличается гибкостью
• Служит причиной развития перфекционизма
• Продуцирует страх публичных выступлений
• Продуцирует страх общения с авторитетами и более осведомленными людьми
• Снижает мотивацию к достижению новых результатов
• Может погрузить человека в одиночество
• Служит причиной проблем в личной, социальной и профессиональной жизни
• Порождает зависимость от других людей и общественного мнения
• Способствует развитию вредных привычек

Поведенческая психология, да и банальный житейский опыт говорят о том, что чем скорее человек осознает иррациональность и нелогичность своих мыслей и действий, тем быстрее в его жизни начнут происходить благоприятные перемены: сократится количество негативных событий и ошибок, станет более крепкой психика и повысится устойчивость к стрессам, повысится личная продуктивность и эффективность, сформируется критический подход к обработке информации.

Мыслить иррационально для здравомыслящего человека неправильно. Но одолеть эту помеху на пути развития критического мышления можно только тогда, когда известны причины ее появления. И о них стоит поговорить детальнее.

Причины иррационального мышления

Для начала стоит сказать о том, что зачастую поведенческие стереотипы закладываются еще в раннем детстве. Они необходимы, т.к. не просто экономят энергию и время на принятие решений, но и способствуют первоначальной адаптации к жизни и обществу, обеспечивая выживание индивида. Но по достижении взрослого возраста человек начинает сталкиваться со «сбоями», т.е. с проблемами иррационального мышления. Основными причинами тому служат следующие:

• Не все мыслительные схемы и механизмы, сформированные в детском возрасте, оказываются верны
• Не все мыслительные схемы и механизмы, подходящие для ребенка, подходят для взрослого человека

Иррационализм является нарушением мышления. Впоследствии это приводит к проблемам адаптации к окружающей действительности. Кроме того, в сознании человека формируются деструктивные базовые установки, а именно:

• Завышенная требовательность к себе (я должен то-то, я не должен того-то)
• Завышенные требования к окружающему миру (они должны то-то, они не должны того-то)
• Катастрофизация (если это случится – это конец, ужас, смерть, катастрофа, все пропало и т.д.)
• Низкая фрустрационная толерантность (я не смогу этого пережить, для меня это конец и т.п.)

Сложив все мысли, приведенные выше, на выходе мы получим нечто вроде: «Я ни в коем случае не должен запнуться во время своего выступления. Если я вдруг запнусь, они не должны поднимать меня на смех. Но если это случится – это означает конец для меня, я этого не переживу».

В действительности многообразие мыслей может быть намного шире, но если отбросить все лишнее, всегда можно увидеть стандартный механизм иррационального мышления, срабатывающий каждый раз в разных ситуациях в измененной форме. Кстати, подобная схема нередко служит причиной всевозможных человеческих страхов.

Любая проблема, любое явление или процесс, при столкновении с которым у человека возникает психологический дискомфорт, можно разобрать на элементы, чтобы найти основную иррациональную схему, вызывающую страх, тревогу, панику и прочие проявления и нарушающие взаимодействие с окружающим миром.

Говоря простым языком, тот, кто не способен различать вымысел и правду, а также находить причинно-следственные связи, использует иррациональное мышление. Оно никогда не поможет предугадать события или просчитать результаты своих действий, отчего и возникают спонтанные поступки и ненужные переживания.

Но и рациональное и критическое мышление в какой-то мере включает в себя иррациональную, можно сказать духовную составляющую. К примеру, люди искусства, создавая уникальные произведения, часто противоречат логическим законам, хотя и действуют обдуманно. Однако иррациональное не должно владеть умом здравомыслящей личности, и с его проявлениями можно и нужно бороться.

Как бороться с иррациональным мышлением

Преодолеть иррационализм непросто, но при должном усердии и систематических тренировках это вполне возможно. Важно лишь знать, что делать. Способов же существует немало, и сейчас мы с ними вас познакомим.

1

Определение иррациональных мыслей

Определять иррациональные мысли сложно только на первом этапе. Часто они появляются в голове очень быстро и автоматически, берутся, словно из ниоткуда, и уловить их осознанно почти нереально. По этой причине задачу можно упростить: заведите себе блокнот, куда в течение дня и ежедневно вы будете записывать мысли, способные вызвать у вас негативные эмоции, тревогу и переживания. С практикой определять их появление станет легко, т.к. ваш мозг будет натренирован и адаптирован к этому.

2

Установление объективности мыслей

Когда вы спокойны, расслаблены и ничто вас не тревожит, задайте себе вопрос: «Насколько объективны мои мысли?». К примеру, кто-то сегодня не захотел с вами общаться, а вы сразу начали себе надумывать не бог весть что. Но посмотрите на ситуацию критически: быть может, он просто устал и был не в духе? А если вы при общении с кем-то проявили немного робости, на самом ли деле этот кто-то составит о вас негативное мнение?

Чтобы лучше осознавать необъективность своих мыслей, воспользуйтесь простым приемом: посмотрите на ситуацию с новой стороны. Т.е. если вы видите, что человек проявляет ту же робость, вы сразу думаете об этом человеке плохо? А если вы не хотите в данный момент с кем-то общаться, это означает, что он вам не нравится? Скорее всего, все обстоит совсем не так. Всегда оценивайте ситуацию с нескольких сторон, и жизнь станет намного проще и интереснее.

3

Подмена иррационального рациональным

Еще один метод – планомерная замена иррациональных мыслей рациональными, более объективными. Но ощутимого результата тут можно ждать лишь через некоторое время. На первых шагах может чувствоваться психологический дискомфорт, но его нужно смело преодолевать ежедневными тренировками. Постепенно новая привычка закрепится и войдет в вашу зону комфорта.

Вот пример хороших мыслей, которыми можно подменить иррациональные: «Вполне возможно он не заметил моей робости», «Мне вообще могло показаться, что она не хочет общаться», «Да они, скорее всего, обо мне даже и не думали» и т.п.

Если обобщить три этих способа, можно сделать такой вывод: например, вам предстоит через несколько минут выйти на контакт с малознакомым человеком. Времени до встречи становится все меньше, а ваша тревога становится все сильнее. И как раз сейчас самое время спросить у себя, почему же вам страшно. Скорее всего, страх связан с тем, что ваш будущий собеседник может заметить какие-то особенности в вашем поведении: слегка неуверенный голос, небольшая дрожь рук и т.д., отчего у него сложится отрицательное представление о вас. Вот здесь-то и стоит применить навыки критического мышления:

• Мысли собеседника могут быть заняты чем-то другим в момент общения
• Собеседник может не заметить особенностей вашего поведения
• Даже если собеседник что-то заметит, он вряд ли будет это анализировать, и через несколько минут уже забудет о вас

Вы и сами видите, что ничего страшного на самом деле нет. Злую шутку играет иррациональное мышление. Но при регулярном проведении подобной процедуры тревожные состояния постепенно начнут отступать и терять силу.

А вот еще несколько хороших приемов борьбы с иррациональным, которые предлагает нам поведенческая психология:

4

Не впадать в крайности

Оценивая какую-то ситуацию, старайтесь избегать крайностей вроде «это точно плохо», «только это – хорошо», «это конец», «так или никак вообще» и т. д. Преодолеть подобные мысли можно несколькими путями:

• Исключить из своего лексикона слова, выражающие крайности, такие как «никогда» или «всегда». Перестаньте использовать эти термины в отношении себя, окружающих людей и мира, в котором живете.
• Принять тот факт, что нет плохих или хороших людей, плохих или хороших ситуаций. В любом человеке и любой ситуации при желании можно найти плюсы и положительные стороны.
• Отказаться от категоричного мышления. Иногда полезно принять себя вместе со своими недостатками и слабостями, чем убеждать себя и других в их отсутствии. Нередко это помогает оправдать свое поведение и мышление.

5

Избегать катастрофичности в мыслях

Преувеличивая масштаб и значимость проблемы, вы делаете хуже самому себе. Говоря о чем-то неприятном, не стоит придавать «не очень хорошо» форму «кошмарно». Отношение к проблемам и неприятностям легко изменить:

• Задумайтесь над тем, что проблемная ситуация пусть и не хороша, но вовсе не ведет к неминуемой гибели и краху всех надежд
• Попробуйте сравнить проблемную ситуацию с чем-то по-настоящему страшным, к примеру, со смертью кого-то из близких, или тем, что чувствуют бездомные или несправедливо заключенные люди

Также можно попытаться самому успокоить себя:

• «На самом деле в этом нет ничего страшного, чтобы так переживать»
• «Да, неприятно, но на этом жизнь не заканчивается»
• «В любом случае все образуется»
• «От этого еще никто не умирал»

6

Размышлять объективно

Если вы замечаете, что вам свойственны преувеличения и иррационализм, и вы часто рисуете себе картины страшных последствий даже при незначительных проблемах, тренируйтесь думать объективно:

• Жизнь преподносит не только испытания, но и радостные события, и за черной полосой всегда последует белая
• Даже если исход какой-то ситуации и может быть плохим, его вероятность крайне низка
• Зачем переживать из-за того, что не случилось? Скорее всего, ничего плохо не произойдет, а тревога – лишь пустая трата энергии
• Моделируйте разные варианты развития событий, а затем прогнозируйте вероятность наступления каждого из них

7

Психически расслабляться

Многих часто посещает мысль «я больше так не могу».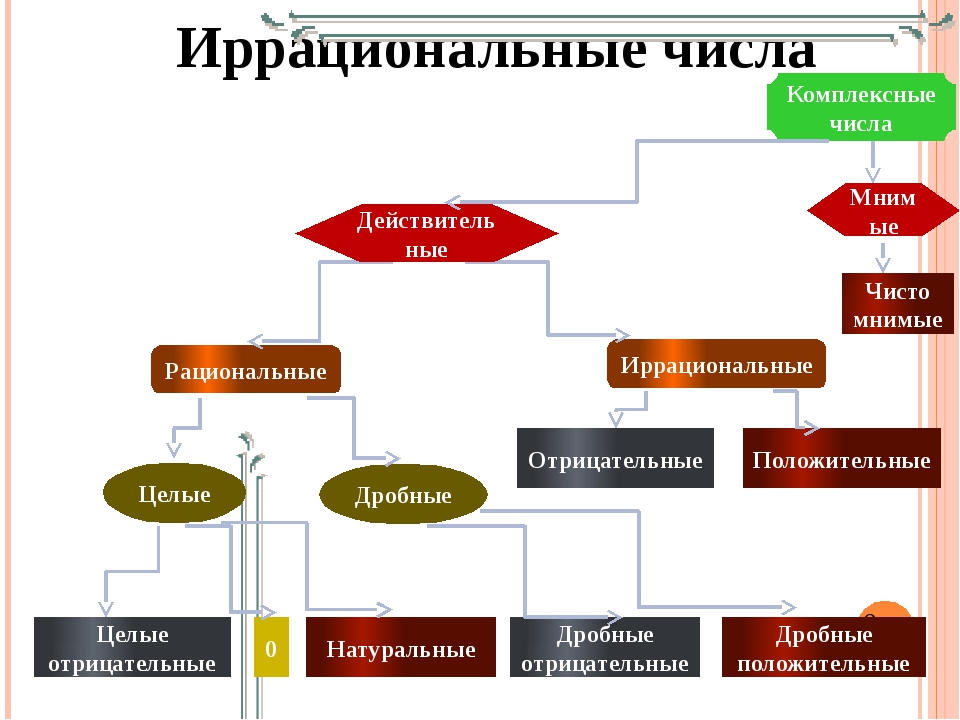 Но это свойственно иррациональным и неуверенным в себе людям. Чтобы побороть иррациональные мысли, нужно переформулировать свое убеждение и убедить себя в том, что, несмотря на сложности в текущий момент, через некоторое время вам станет легче и вы решите свои проблемы.

И, подытоживая этот раздел, осталось сказать только, что самым эффективным способом преодолеть иррационализм и негативные переживания является критический подход: ставьте под сомнение свои чувства и ощущения и анализируйте нелогичные и иррациональные мысли, лежащие в их основе.

Иррациональное мышление порождается желанием человека верить в свои фантазии. Это почти бессвязные рассуждения, не имеющие никаких логических обоснований и основанные на чувствах и предположениях. Рациональное и критическое мышление, напротив, состоит в том, что за основу размышлений и будущих действий берутся только обоснованные логикой и причинно-следственными связями факты и свидетельства. Польза и эффективность такого подхода очевидна и неоспорима, но вы все-таки скажем о ней несколько слов.

Преимущества рационального мышления

Рациональное мышление помогает делать выводы и принимать решения, используя для этого логические цепочки. Желание мыслить критически и рационально способствует работе над своими недостатками. Когда в расчет берутся логические размышления, человек перестает совершать спонтанные поступки, а это минимизирует возникновение неприятных неожиданностей.

Когда мы мыслим рационально, мы начинаем видеть вещи такими, какие они есть, можем объяснить то, что раньше казалось необъяснимым, становимся более спокойными и находим наиболее короткие и эффективные пути достижения своих целей, получаем возможность фокусироваться на наиболее приоритетных в данный момент вещах.

Научиться рационально мыслить не составляет никакого труда. Все, что нужно – следовать небольшому ряду простых правил и советов:

• Все размышления должны начинаться с поиска достоверной информации. Не всегда это бывает просто, но выстраивать логические цепочки, ведущие к правильным выводам и действиям, без проверенных данных невозможно.
• Размышляя о чем-то, всегда брать в расчет то, что неверной может быть не только позиция другого человека, но и ваша собственная. Интересуйтесь у окружающих, что они думают о предмете ваших мыслей. Это позволит взглянуть на ситуацию с разных ракурсов.
• Не берите за основу своих суждений о действиях и поведении окружающих лишь внешние проявления. Вы уверены, что человек не желает с вами общаться? На чем основывается такой вывод? На домыслах или логике? Догадки еще ничего не значат. Вы должны стремиться к выяснению правды. Когда хотите убедиться в чем-то, ищите подтверждающие это факты.
• Никогда не додумывайте за человека и не принимайте за него решения, не пытайтесь прочитать его мысли. Одно из правил эффективного общения – внимательно слушать своего собеседника и воспринимать только то, что он говорит.
• Если при общении с человеком у вас возникают сомнения в искренности его поступков и слов, просто задайте ему несколько прямых вопросов, выскажите беспокоящие вас мысли и попробуйте пообщаться доверительно.

Преимущества рационального мышления можно наглядно продемонстрировать на таком примере: вы пообщались с человеком и он озвучил вам свои недовольства и упреки, объяснил, что ваши взгляды и действия для него неприемлемы. Первое, что хочется сделать в ответ, – это отплатить той же монетой. Однако что будет в результате, кроме недопонимания, ссор и неприязни? Возможно, еще больше душевного дискомфорта и долгосрочный разрыв отношений.

Намного эффективнее будет постараться сохранить спокойствие, равновесие и собственное достоинство. И рациональное мышление предлагает в этом случае поступить гораздо проще: проанализировать свои действия и слова, вызвавшие критику и недовольство собеседника, и принять критическое мнение со стороны. Нужно приходить к компромиссу – искать взаимопонимания и согласия по вопросу, на который у вас имеются разные взгляды. Одновременно с этим следует дать понять другому человеку, что проблемные ситуации могут быть разрешены без унижений, скандалов и обид, и для вас это приемлемо.

Рациональный подход и развитие критического мышления будут способствовать тому, что вы вернете себе спокойствие и психологический комфорт. В любой ситуации, когда вы оказываетесь во власти иррациональных мыслей, вызванных эмоциями, усталостью, переутомлением или стрессами, как можно скорее прогоняйте их от себя.

Не важно, кто вы: химик, физик, математик, военный, бизнесмен, простой работник фирмы или студент, рациональное и критическое мышление может стать для вас эффективным средством для достижения целей, решения повседневных и профессиональных задач, улучшения общения с людьми и взаимодействия с окружающим миром, самопознания и развития своих способностей.

Чтобы повысить свой иммунитет к иррациональным мыслям, мы рекомендуем вам вести здоровый образ жизни, больше отдыхать, правильно спать, развивать мозг и культивировать в себе хорошее настроение и позитивный настрой. И, конечно, читайте соответствующую литературу: Даниэль Канеман «Думай медленно, решай быстро», Кейт Станович «Рациональное мышление. Что не измеряют тесты способностей», Дайана Халперн «Психология критического мышления», Роберт Бертон «Разум VS Мозг. Разговор на разных языках» и другие книги.

И в заключительном уроке нашего курса мы коснемся еще одного важного вопроса, касающегося критического мышления – работы с информацией. Именно с ней нам приходится сталкиваться каждый день, и от ее достоверности зависят наши выводы и суждения, эффективность принимаемых решений и грамотность действий. Из шестого урока вы узнаете, как искать информацию, как ее анализировать и хранить, для каких целей может применяться информация, как с ней работать и как принимать решения на ее основе.

Хотите проверить свои знания?

Если вы хотите проверить свои теоретические знания по теме курса и понять, насколько он вам подходит, можете пройти наш тест. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу.

Кирилл Ногалес

Иррациональные числа — урок.

Алгебра, 8 класс.

Термины рациональное число, иррациональное число происходят от латинского слова ratio — разум
(буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).

Иррациональным числом называют бесконечную десятичную непериодическую дробь.

Если натуральное число \(n\) не является точным квадратом, т. е. n≠k2, где k∈ℚ, то  n — иррациональное число.

Пример:

5=2,23606798…11=3,31662479…

Иррациональные числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чём вы не раз убедитесь в старших классах.

Если длину любой окружности разделить на её диаметр, то в частном получится иррациональное число \(3,141592. ..\) Для этого числа в математике введено специальное обозначение π (буква греческого алфавита «пи»; версия происхождения этого понятия такова: с буквы π начинается греческое слово периферия — окружность). Иррациональность числа π была доказана в \(1766\) г. немецким математиком И. Ламбертом.

Итак,

1. любая арифметическая операция над рациональными числами (кроме деления на \(0\)) приводит в результате к рациональному числу.

2. Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу.

3. Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на \(0\)).

4. Поскольку операция извлечения квадратного и кубического корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного и кубического корня из переменной, называть иррациональным выражением.

Рациональное и иррациональное в культуре

• Павел Гуревич Институт философии Российской академии наук. 109240, Российская Федерация, Москва, ул. Гончарная, д. 12, стр. 1

Ключевые слова: искусство, рациональность, иррациональность, разум, культура, миф, религия, традиция, ценность, сознание

Аннотация

Автор статьи стремится охарактеризовать рационалистическую версию культуры. Он отмечает, что культура несёт в себе огромное содержание. Её наполнение кажется безграничным. Она возникает благодаря тому, что разум человека даёт ему возможность особыми, неизвестными природе способами добывать, сохранять, накапливать, обрабатывать и использовать информацию. Эти способы связаны с созданием специальных знаковых систем, с помощью которых информация кодируется и транслируется в социуме. Культура прежде всего сверхприродна. В природе нет звучащих симфоний, стихотворных лирических излияний, пейзажей, схваченных анонимной кистью. Человек творит культуру, опираясь на собственное сознание, эмоции, волю и интуицию. Она предназначена для сотворения неизведанных миров. Поэтому, описывая культуру конкретной эпохи, мы в первую очередь называем достижения науки, философии, искусства.

Эти установки вдохновляли возникшую в XVIII в. особую область философского знания – философию культуры. Однако философия расширила границы культуры, её многосоставность и обратилась к анализу глубинных основ человеческого существования, обосновала плодоносность традиции и кристаллизации человеческого опыта, приступила к аналитике бессознательного.

Автор полагает, что спектр культуры неистощим, но он не исчерпывается рациональностью, разумностью. Её исток не только сознание. Культура всеохватна. Многие её формы рождены бессознательным пластом человеческой психики, наитием, игрой воображения, эмоциональной отзывчивостью. Разумеется, рационалистическое ядро является стержнем культуры. Рациональное может рассматриваться как универсальная категория, охватывающая чистую логику в классическом и современном мышлении и даже некоторые формы мистического опыта. Однако этот тезис о едва ли не всеохватном смысле понятия «рациональность» требует критического рассмотрения.

Скачивания

Данные скачивания пока недоступны.

Биография автора

Павел Гуревич, Институт философии Российской академии наук. 109240, Российская Федерация, Москва, ул. Гончарная, д. 12, стр. 1

Павел ГУРЕВИЧ — доктор философских наук, доктор филологических наук, профессор, главный научный сотрудник сектора истории антропологических учений. Институт философии Российской академии наук.

Рациональные и иррациональные суждения | Элитариум

Рациональная жизнь включает в себя такие мышление, чувства и поведение, которые способствуют достижению выбранных целей. В свою очередь, нерациональность подразумевает мышление, чувства и поведение, препятствующие достижению поставленных целей. Рациональная жизнь предполагает поддержание разумного баланса. Иррациональные убеждения ведут к возникновению проблем. Что же делать с иррациональными суждениями? Их следует заменять рациональными и вырабатывать эффективную жизненную философию.

Автор:

Александр Николаевич Tapacoв, доктор психологических наук, заместитель заведующего кафедрой социологии и психологии управления Государственного университета управления.

 

Американский психотерапевт Альберт Эллис разработал концепцию рационально-эмотивной терапии (РЭТ), целью которой является изменение внутренних убеждений, становящихся причиной возникновения эмоциональных проблем. Суть ее состоит в следующем.

Фактически все люди имеют

три фундаментальные цели: выжить, быть относительно свободными от боли и быть в разумных пределах удовлетворенными или довольными. Кроме того, они руководствуются первичными целями — хотят быть счастливыми:

• сами по себе;
• в общении с другими людьми;
• интимно, с некоторыми избранными другими людьми;
• в сфере информации и образования;
• профессионально и экономически;
• в сфере отдыха и развлечений.

Рациональная жизнь включает в себя такие мышление, чувства и поведение, которые способствуют достижению выбранных целей. В свою очередь, нерациональность подразумевает мышление, чувства и поведение, препятствующие достижению поставленных целей. Рациональная жизнь предполагает поддержание разумного баланса между удовольствиями «здесь и теперь» и удовольствиями более длительного действия, получаемыми за счет дисциплины в настоящем.

Иррациональные убеждения ведут к возникновению эмоциональных проблем. Наиболее важные из них — это убеждения в том, что человеку необходимы одобрение и любовь со стороны

всех, с кем ему так или иначе приходится считаться, и убеждение в том, что человек, состоявшийся как личность, должен всегда вести себя

адекватно, быть со всеми компетентным, а также быть способным всегда добиваться решения любых стоящих перед ним задач.

Эти убеждения действуют на личность разрушительно, поскольку ведут к эмоциональным расстройствам всякий раз, когда их обладателю отказывают в одобрении и любви или когда он терпит неудачу в каком-либо начинании. Но ведь такие случаи абсолютно неизбежны и совершенно обычны, поэтому приверженность иррациональной системе убеждений — это гарантия бесконечных разочарований.

Определить рациональное и иррациональное суждение можно по нескольким признакам.

Признаки рационального суждения:

• Истинность и подтверждение опытом. Например: Все предметы, ничем не поддерживаемые, падают вниз.

• Относительность. Например: Оценку четыре по пятибалльной шкале на экзамене кто-то посчитает отличной, а кто-то удовлетворительной. Хотя сама четверка — только цифра, и лишь наши суждения по ее поводу ведут к тому, что мы или печалимся, или радуемся.

• Умеренность, то есть суждение не вызывает сильных эмоций.

• Эффективность (помогает достичь цели).

Признаки иррационального суждения:

• Неистинность. Например: «Я не переживу, если не сдам экзамен».

• Категоричность. Например: «Я должен…», «Мне должны…», «Мир должен…».

• Связь с сильными эмоциональными проявлениями: бурные слезы или смех, яростный гнев и т. п.

• Неэффективность (не помогает достичь цели).

Иначе говоря, иррациональные суждения:

1. Развиваются до катастрофических размеров, например: «Я не переживу…»
2. Включают элемент долженствования: «Я должен», «Я обязан», «Мне должны».
3. Включают элемент оценки: хорошо — плохо; правильно — неправильно.

А. Эллис представил связь между нашим мышлением, эмоциями и поведением следующим образом:

• Во-первых, мышление и эмоции связаны.
• Во-вторых, они связаны так тесно, что обычно сопровождают друг друга, действуя в круговороте отношений «причина и следствие», так что мышление превращается в эмоцию, а эмоция становится мыслью.
• В-третьих, и мышление, и эмоции имеют тенденцию принимать форму саморазговора или внутренних предложений, проговариваемых людьми про себя, которые, в свою очередь, являются или становятся их мыслями и эмоциями.

Кроме того,

мышление и эмоции связаны с поведением. Схема этой взаимосвязи выглядит следующим образом:

А — С — П,

где А — активирующее событие, то есть информация, полученная из внешнего мира; С — суждение, то есть интерпретация полученной информации и ее оценка; П — последствия, то есть реакция на «А», выраженная через эмоции и поведение.

Важно отметить, что информация, полученная из внешнего мира, сама по себе не определяет нашу реакцию, выраженную через эмоции и поведение. На чувства и поведение влияет

исключительно наше суждение по поводу этой информации.

В качестве примера рассмотрим следующую ситуацию.

Человек сталкивается с таким активирующим событием «А», как потеря одобрения своих действий. Если по этому поводу у него имеется следующее убеждение «С»: «Я предпочитаю, чтобы меня одобряли, но это не обязательно», то он воспринимает данное событие как несерьезную обиду. Однако, имея убеждение: «Меня должны одобрять, в противном случае я ничего не стою», он будет воспринимать произошедшее событие «А» как безжалостное преднамеренное оскорбление. В таком случае его поведение «П» может быть следующим: человек почувствует себя угнетенным и, вполне возможно, начнет избегать тех, кто не одобряет его действий.

Суждения, которые способствуют проявлению неадекватного поведения, или неконструктивных эмоций, связаны с такими критериями оценки событий, как «это плохо»; «я должен, обязан», «мне должны, обязаны»; «это ужасно, я ничего не стою»; «я глупый» и т. п. Часто такие суждения способствуют нарушению душевного равновесия, которое является результатом следования установке «Я должен преуспеть и добиться одобрения всеми моих действий». Обычно люди, имея такую установку, думают о себе как о неполноценных и недостойных личностях и ощущают себя таковыми тогда, когда они действуют не так хорошо, как, по их мнению, они должны были действовать.

А. Эллис расценивает это качество как чрезмерную претензионность, стремление быть богоподобными, поскольку люди, предъявляющие к себе повышенные требования, желают быть особенными, совершенными, выдающимися — в общем, сверхлюдьми. Затем они двигаются дальше к иррациональным убеждениям (одному или сразу двум): «Другие должны быть со мной внимательны и любезны», «Условия, в которых я живу, должны быть такими, чтобы я получал фактически все, что хочу, причем быстро и легко». Нагнетание страха и «болезнь», которую можно назвать «Я не могу этого выдержать», являются производными таких установок. В основном при нарушении душевного равновесия люди настаивают таким образом: «Моя жизнь должна быть легкой, я должен быть совершенным человеком, условия жизни должны быть всегда благоприятными для меня, а люди всегда должны соответствовать моим взглядам и угождать мне, мне, мне, мне!»

Что же делать с иррациональными суждениями? Их следует заменять рациональными и вырабатывать эффективную жизненную философию. В таком случае формула принимает несколько иной вид:

А — С — П — Д — Э,

где Д — дискуссия, спор, ведущие к замене иррационального суждения на рациональное, истинное; Э — эффективная философия жизни.

Рассмотрим распространенные иррациональные суждения.

1. Меня должны любить и поддерживать те, кто мне небезразличен, а если нет — то это ужасно. (Ошибочность этого утверждения мы подробно обсудили выше.)

2. Когда люди поступают нечестно и плохо, они — омерзительные личности. (Здесь мы переносим оценку поступка на личность, в результате портим отношения с людьми, вместо того чтобы обсуждать возникшую проблему, говорить конкретно о ней, а не о качествах личности человека.)

3. Это ужасно, когда дела идут не так, как я хотел(а) бы. (Речь идет о непринятии человеком произошедшей с ним жизненной ситуации, о желании сразу получать удовольствие, о непереносимости отсрочки достижения желаемого результата. )

4. Мне следует быть осторожным и избегать в отношениях неопределенных ситуаций. (В основе суждения — страх познания нового, личных изменений и связанного с этим дискомфорта.)

5. Я ничего не стою, если не добиваюсь успехов всегда, когда мне этого хочется, или не всегда компетентен(а). (В основе лежат убеждения: «Я должен быть совершенным», «Я должен полностью контролировать ситуацию», что, конечно же, невозможно и ведет к повышению тревожности, возникновению у человека невроза.)

6. Мир должен быть честным и справедливым. (Претензии к миру обычно сопровождаются обидой или агрессией, которые разрушительно действуют на самого человека. Необходимо научиться принимать создавшиеся ситуации как потенциальные уроки и делать выводы, изменяясь внутренне.)

7. У меня не должно быть дискомфорта и боли. (Это суждение уже анализировалось нами.)

8. Я нуждаюсь в ком-то более сильном, чем я, чтобы на него положиться. (В основе лежит нежелание брать ответственность за свою жизнь на себя, несамостоятельность.)

9. Прошлое — причина моих сегодняшних проблем. (Раз проблема есть сегодня, значит, и причину нужно искать в настоящем и находить способы и возможность ее решить).

Таким образом, ситуация, в которой мы находимся, оценивается исключительно нами. Наличие у человека проблемы означает, что его взгляд на жизнь нерационален и ему необходимо обнаружить свое иррациональное суждение и переработать в рациональное, то есть найти альтернативу и принять новую жизненную философию. Причем смена одного суждения на другое предполагает глубокое изучение проблемы, ее понимание, способность в ней разобраться, а не сводится к ее игнорированию, выбрасыванию из головы.

Как показывает

А. М. Прихожан (2001), люди, имеющие негативное отношение к жизни, ведущее их к неуверенности в себе, часто придерживаются следующих взглядов:

1. Всегда и везде жди от себя только неприятностей (больших и маленьких).
2. Если на тебя неожиданно свалится успех, сделай все, чтобы его не замечать, или, уж если это совсем невозможно, убеждай себя и всех вокруг, что это, конечно же, случайно, по ошибке и скоро все кончится.
3. Будь во всем последовательным и принципиальным. Ни за что и никогда не меняй своих решений и не отступай от своих принципов.
4. Выбери одно из двух — или придерживайся чужих советов, или действуй напролом, как придется. Самое главное — не обращай внимания на то, что в действительности происходит.
5. Изо всех сил уклоняйся от возможностей проверить себя, свои способности. Избегай трудных ситуаций.
6. Со страстью занимайся коллекционированием своих бед и неприятностей. Холь и лелей каждую, ни об одной не забывай. Относись к каждой из них, как к своему личному достоянию.
7. Побольше занимайся самооправданиями. Помни: поиск самооправдания и того, на кого можно свалить вину, — одно из основных интеллектуальных занятий истинного неудачника. Во всех случаях задавай вопрос «Кто виноват?» и никогда — «Что делать?».
8. Относись ко всему как можно серьезнее. Не позволяй себе легкомысленного взгляда на вещи.
9. Рассматривай каждый неуспех как окончательное поражение, которое окажет решающее влияние на всю твою дальнейшую жизнь.
10. Избегай любви к себе.

Отмечено, что позитивный и негативный настрой мыслей, позитивное и негативное отношение к жизни действует как своего рода магнит, притягивая к их хозяину положительные или отрицательные события.

Домашнее задание

1. В течение следующей недели рассматривайте все, что с вами происходит, так, как если бы все события требовали от вас

   выбора или сознательного решения о наиболее удачной стратегии поведения. Так, прежде, чем что-либо сделать, спросите себя: «Действительно ли я хочу сделать это сейчас или я желаю сделать что-то другое?» Только ответив на этот вопрос, принимайте решение. Таким образом вы сэкономите время и совершите более необходимые для себя действия. Вечером перед сном проанализируйте эффективность такой стратегии, опираясь на свои впечатления.

2. Как можно дольше

   живите с положительным отношением к жизни, то есть с чувствами уверенности, активности, оптимизма. Помочь вам в этом могут самые разные упражнения. Например, можно посмотреть в зеркало, подмигнуть себе и либо улыбнуться и произнести утверждение, которое вызовет у вас чувство уверенности, например: «Я могу!», «Я способен(а) добиться того, чего хочу!», «Я победитель!», «Моя жизнь принадлежит мне!», «Мне нравится мир и люди вокруг!» — любую формулу, которую вы найдете для себя сами и которая в наибольшей степени поможет вам сохранить веру в себя.

3. Действуйте, сохраняя на губах улыбку, а внутри —

   ощущение собственной силы и возможностей. Для этого используйте следующий прием: вспомните ситуацию, когда вы чувствовали себя уверенно, и почувствуйте энергию этого состояния в теле. Сохраняйте ощущение уверенности как можно дольше. Пусть это поначалу будет лишь краткими эпизодами в течение дня, главное, чтобы вы поняли и почувствовали это состояние.

Всякий человек может и должен жить с ощущением уверенности в своих силах, которая рождает доброжелательное и открытое отношение к окружающему миру.

Научитесь рациональному и выгодному для себя поведению не только в конфликтах, но и в повседневных рабочих ситуациях. При обучении по индивидуальной программе, при помощи опытного куратора, вы можете составить индивидуальный учебный план из десятков учебных курсов нашего каталога, изучив сотни практических навыков в удобном для себя темпе, времени и месте.

Какие числа называются Иррациональные?

Определение иррациональных чисел

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры иррациональных чисел:

• π = 3,1415926…
• √2 = 1,41421356…
• e = 2,71828182…
• √8 = 2.828427…
• -√11= -3.31662…

Множество иррациональных чисел договорились обозначать латинской буквой I.

Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Если натуральное число n не является точным квадратом, т. е. n ≠ k², где k ∈ Q, то √n — иррациональное число.

Свойства иррациональных чисел

Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.

Свойства иррациональных чисел:

• результат суммы иррационального числа и рационального равен иррациональному числу;
• результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
• результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
• результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

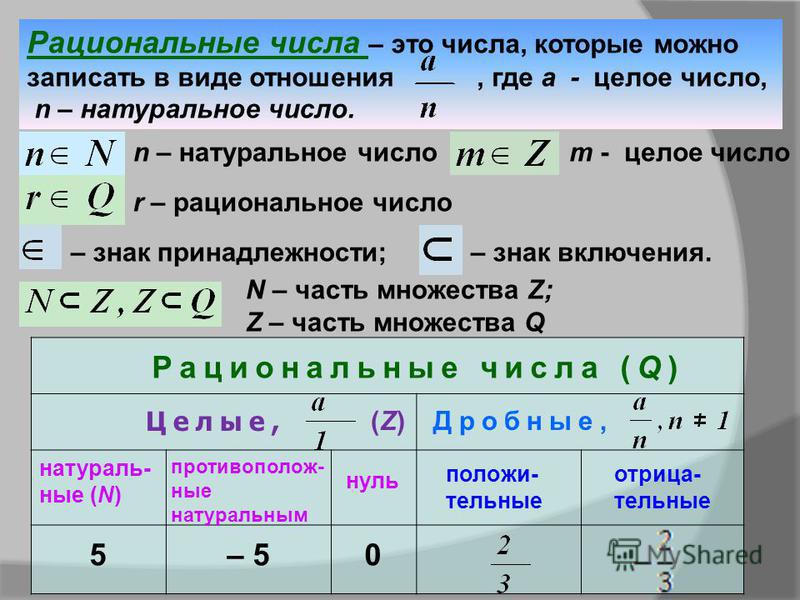
Определение рациональных чисел

А теперь наоборот: рассмотрим противоположное заданной теме определение.

Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.

Рациональные числа —  это те, которые можно представить в виде:

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

• десятичная дробь 1,15 — это 115/100;
• десятичная дробь 0,2 — это 1/5;
• целое число 0 — это 0/1;
• целое число 6 — это 6/1;
• целое число 1 — это 1/1;
• бесконечная периодическая дробь 0,33333. .. — это 1/3;
• смешанное число это 25/10;
• отрицательная десятичная дробь -3,16 — это -316/100.

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами Переместительное свойство сложения: a + b = b + a. Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Запутаться в числах — плевое дело, но только не в школе Skysmart. Ученикам помогают красочные персонажи интерактивной платформы и заботливые учителя.

Приходите на бесплатный вводный урок математики вместе с ребенком: покажем, как у нас все устроено, порешаем задачки и вдохновим на учебу!

Определение рациональных и иррациональных чисел

Результаты обучения

• Определить рациональные числа из списка чисел
• Определите иррациональные числа из списка чисел

В этой главе мы позаботимся о том, чтобы ваши навыки твердо закрепились. Мы еще раз взглянем на типы чисел, с которыми работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа.И мы будем практиковаться в их использовании, как при решении уравнений и выполнении других процедур в алгебре.

Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?

счетные числа	[латекс] 1,2,3,4 \ точки [/ латекс]
целые числа	[латекс] 0,1,2,3,4 \ точки [/ латекс]
целые числа	[латекс] \ точки -3, -2, -1,0,1,2,3,4 \ точки [/ латекс]

Рациональные числа

Какой тип чисел вы получите, если начнете со всех целых чисел, а затем включите все дроби? Числа, которые у вас получились бы, составили набор рациональных чисел.Рациональное число — это число, которое можно записать как отношение двух целых чисел.

Рациональные числа

Рациональное число — это число, которое может быть записано в форме [латекс] \ frac {p} {q} [/ latex], где [latex] p [/ latex] и [latex] q [/ latex] — целые числа. и [латекс] q \ ne o [/ латекс].

Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров:

[латекс] \ frac {4} {5}, — \ frac {7} {8}, \ frac {13} {4}, \ text {and} — \ frac {20} {3} [/ latex]

Каждый числитель и каждый знаменатель — целое число.

Нам нужно посмотреть на все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Целые числа являются рациональными числами? Чтобы решить, является ли целое число рациональным числом, мы пытаемся записать его как отношение двух целых чисел. Легкий способ сделать это — записать дробь со знаминателем один.

[латекс] 3 = \ frac {3} {1} -8 = \ frac {-8} {1} 0 = \ frac {0} {1} [/ latex]

Поскольку любое целое число можно записать как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа также являются целыми числами, а значит, они тоже рациональны.

А как насчет десятичных знаков? Они рациональны? Давайте посмотрим на некоторые из них, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа являются рациональными числами. Целое число [латекс] -8 [/ латекс] может быть записано как десятичное [латекс] -8,0 [/ латекс]. Итак, очевидно, что некоторые десятичные дроби рациональны.

Подумайте о десятичном [латексе] 7.3 [/ латексе]. Можем ли мы записать это как отношение двух целых чисел? Потому что [латекс] 7.3 [/ latex] означает [latex] 7 \ frac {3} {10} [/ latex], мы можем записать это как неправильную дробь, [latex] \ frac {73} {10} [/ latex]. Итак, [latex] 7.3 [/ latex] — это соотношение целых чисел [latex] 73 [/ latex] и [latex] 10 [/ latex]. Это рациональное число.

В общем, любое десятичное число, которое заканчивается рядом цифр, например [latex] 7.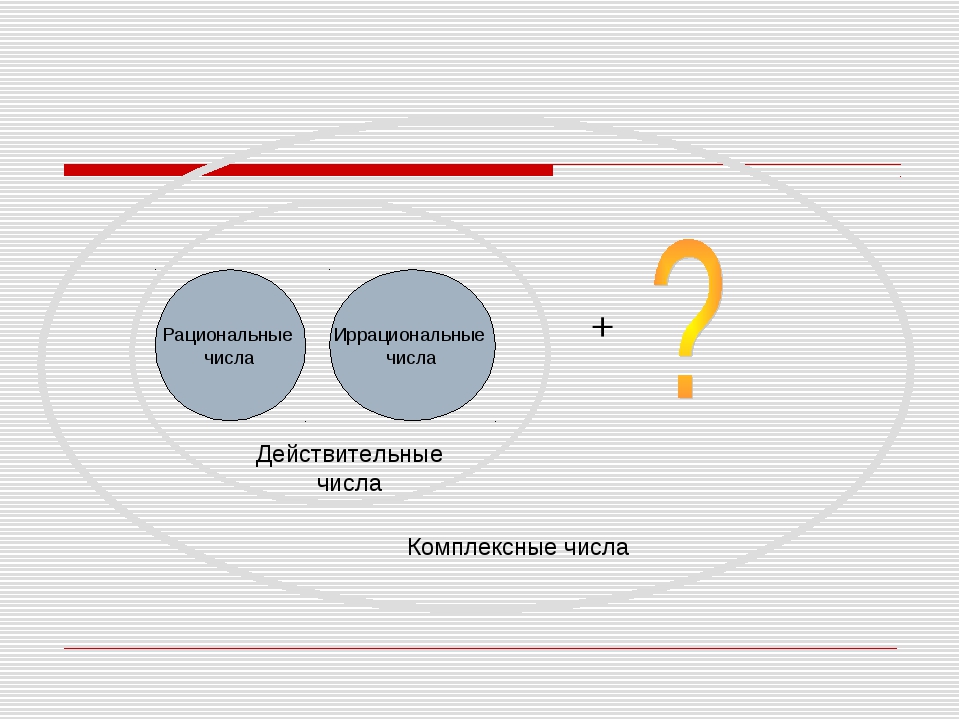 3 [/ latex] или [latex] -1.2684 [/ latex], является рациональным числом. Мы можем использовать разряд последней цифры в качестве знаменателя при записи десятичной дроби в виде дроби.

пример

Запишите каждое как отношение двух целых чисел:

1. [латекс] -15 [/ латекс]

2. [латекс] 6.81 [/ латекс]

3. [латекс] -3 \ frac {6} {7} [/ латекс]

Решение:

1.
	[латекс] -15 [/ латекс]
Запишите целое число в виде дроби со знаминателем 1.	[латекс] \ frac {-15} {1} [/ латекс]

2.
	[латекс] 6,81 [/ латекс]
Запишите десятичную дробь как смешанное число.	[латекс] 6 \ frac {81} {100} [/ латекс]
Затем преобразовать его в неправильную дробь.	[латекс] \ frac {681} {100} [/ латекс]

Рациональные числа
	Фракции	Целые числа
Номер	[латекс] \ frac {4} {5}, — \ frac {7} {8}, \ frac {13} {4}, \ frac {-20} {3} [/ latex]	[латекс] -2,1,0,1,2,3 [/ латекс]
Коэффициент целого числа	[латекс] \ frac {4} {5}, \ frac {-7} {8}, \ frac {13} {4}, \ frac {-20} {3} [/ latex]	[латекс] \ frac {-2} {1}, \ frac {-1} {1}, \ frac {0} {1}, \ frac {1} {1}, \ frac {2} {1} , \ frac {3} {1} [/ latex]
Десятичное число	[латекс] 0. 8, -0,875,3,25, -6. \ Overline {6} [/ латекс]	[латекс] -2.0, -1.0,0.0,1.0,2.0,3.0 [/ латекс]

Иррациональные числа

Есть ли десятичные дроби, которые не останавливаются и не повторяются? Да. Число [латекс] \ пи [/ латекс] (греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не останавливается и не повторяется.

[latex] \ pi = \ text {3.141592654 …….} [/ Latex]
Точно так же десятичные представления квадратных корней чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются.Например,

[latex] \ sqrt {5} = \ text {2.236067978… ..} [/ latex]
Десятичное число, которое не останавливается и не повторяется, не может быть записано как отношение целых чисел. Мы называем такое число иррациональным числом.

Иррациональное число

Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не останавливается и не повторяется.

Давайте резюмируем метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа

• остановок или повторений, количество рациональное.
• не останавливается и не повторяется, цифра иррациональна.

пример

Определите каждое из следующего как рациональное или иррациональное:
1. [латекс] 0,58 \ overline {3} [/ латекс]
2. [латекс] 0,475 [/ латекс]
3. [латекс] 3,605551275 \ точки [/ латекс ]

Показать решение

Решение:
1. [latex] 0.58 \ overline {3} [/ latex]
Полоса над [latex] 3 [/ latex] указывает на то, что это повторяется.Следовательно, [латекс] 0,58 \ overline {3} [/ latex] является повторяющимся десятичным числом и, следовательно, является рациональным числом.

2. [latex] 0,475 [/ latex]
Эта десятичная дробь останавливается после [latex] 5 [/ latex], так что это рациональное число. {2} = 36 [/ латекс].{2} = 49 [/ latex], поэтому [latex] 44 [/ latex] не является идеальным квадратом.
Это означает, что [latex] \ sqrt {44} [/ latex] нерационально.

В следующем видео мы покажем больше примеров того, как определить, является ли число иррациональным или рациональным.

Рациональные и иррациональные числа | Алгебраические выражения

1.3 Рациональные и иррациональные числа (EMA4)

Рациональное число

Рациональное число (\ (\ mathbb {Q} \)) — это любое число, которое можно записать как:

\ [\ frac {a} {b} \]

, где \ (a \) и \ (b \) — целые числа, а \ (b \ ne 0 \).

Следующие числа являются рациональными числами:

\ [\ frac {10} {1} \; ; \; \ frac {21} {7} \; ; \; \ frac {-1} {- 3} \; ; \; \ frac {10} {20} \; ; \; \ frac {-3} {6} \]

Мы видим, что все числители и все знаменатели целые.

Это означает, что все целые числа являются рациональными числами, потому что они могут быть записаны со знаменателем \ (\ text {1} \).

Иррациональные числа

Иррациональные числа (\ (\ mathbb {Q} ‘\)) — это числа, которые нельзя записать в виде дроби с числителем и знаменателем в виде целых чисел.

Примеры иррациональных чисел:

\ [\ sqrt {2} \; ; \; \ sqrt {3} \; ; \; \ sqrt [3] {4} \; ; \; \число Пи \; ; \; \ frac {1 + \ sqrt {5}} {2} \]

Это не рациональные числа, потому что числитель или знаменатель не является целым числом.

Десятичные числа (EMA5)

Все целые числа и дроби с целыми числителями и ненулевым целым знаменателем являются рациональными числами. Помните, что когда знаменатель дроби равен нулю, дробь не определена.

Вы можете записать любое рациональное число в виде десятичного числа, но не все десятичные числа являются рациональными числами. Эти типы десятичных чисел являются рациональными числами:

• Десятичные числа, которые заканчиваются (или заканчиваются). Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).

• Десятичные числа, состоящие из одной повторяющейся цифры. Например, дробь \ (\ frac {1} {3} \) может быть записана как \ (\ text {0,} \ dot {3} \) или \ (\ text {0,} \ overline {3} \).Обозначения точки и полосы эквивалентны и оба представляют собой повторяющиеся символы \ (\ text {3} \), то есть \ (\ text {0,} \ dot {3} = \ text {0,} \ overline {3} = \ text {0,333 …} \).

• Десятичные числа, повторяющиеся из нескольких цифр. Например, дробь \ (\ frac {2} {11} \) также может быть записана как \ (\ text {0,} \ overline {18} \). Полоса представляет собой повторяющийся узор из \ (\ text {1} \) и \ (\ text {8} \), то есть \ (\ text {0,} \ overline {18} = \ text {0 , 181818. ..} \).

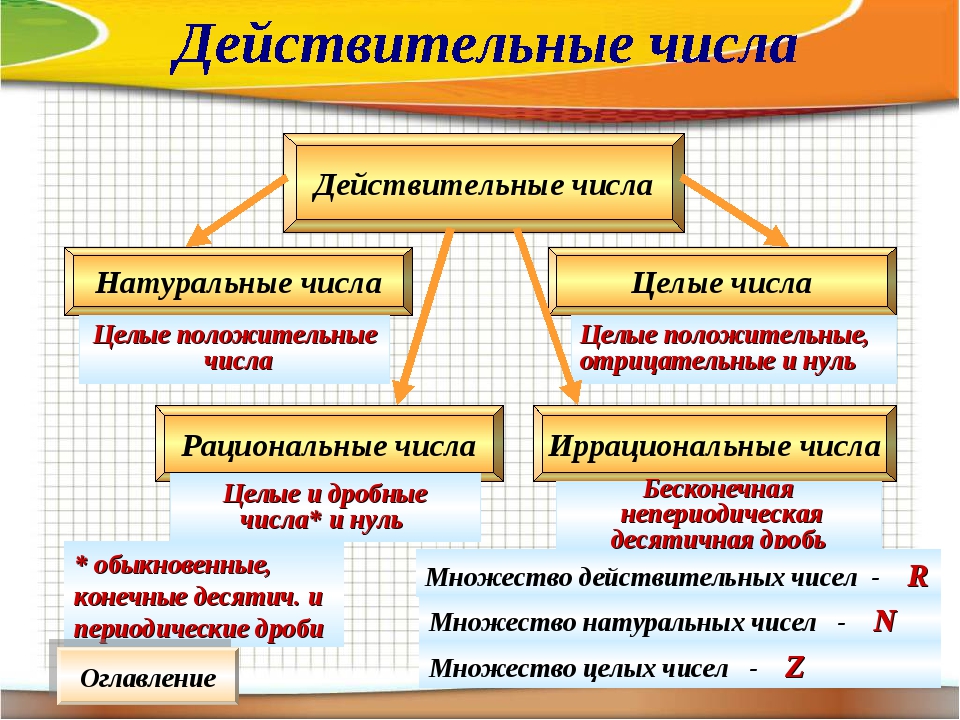Вы можете увидеть точку вместо запятой, используемой для обозначения десятичного числа. Таким образом, число \ (\ text {0,4} \) также можно записать как 0,4

Обозначение: Вы можете использовать точку или полосу над повторяющимися цифрами, чтобы указать, что десятичная дробь является повторяющейся десятичной. Если полоса охватывает более одной цифры, то все числа под полосой повторяются.

Если вас просят определить, является ли число рациональным или иррациональным, сначала запишите число в десятичной форме.Если число заканчивается, то это рационально. Если так будет продолжаться вечно, ищите повторяющийся набор цифр. Если нет повторяющегося рисунка, то цифра иррациональна.

Когда вы записываете иррациональные числа в десятичной форме, вы можете продолжать записывать их для многих, многих десятичных знаков. Однако это неудобно и часто необходимо округлять.

Округление иррационального числа делает его рациональным числом, которое приближается к иррациональному числу.

Рабочий пример 1: Рациональные и иррациональные числа

Какие из следующих чисел не являются рациональными?

1. \ (\ pi = \ text {3,14159265358979323846264338327950288419716939937510 …} \)

2. \ (\ text {1,4} \)

3. \ (\ text {1,618033989…} \)

4. \ (\ text {100} \)

5. \ (\ text {1,7373737373 …} \)

6. \ (\ text {0,} \ overline {02} \)

1. Иррациональная, десятичная дробь не прерывается и не повторяется.

2. Рациональное, десятичное завершение.

3. Иррациональная, десятичная дробь не прерывается и не повторяется.

4. Рационально, все числа рациональны.

5. Рациональный, десятичный имеет повторяющийся образец.

6. Рациональное десятичное число имеет повторяющийся образец.

Преобразование конечных десятичных знаков в рациональные числа (EMA6)

Десятичное число состоит из целой и дробной части. Например, \ (\ text {10,589} \) имеет целую часть \ (\ text {10} \) и дробную часть \ (\ text {0,589} \), потому что \ (10 ​​+ \ text {0,589} = \ текст {10,589} \).

Каждая цифра после десятичной точки представляет собой дробь со знаменателем в возрастающей степени \ (\ text {10} \).

Например:

• \ (\ text {0,1} \) равно \ (\ frac {1} {\ text {10}} \)

• \ (\ text {0,01} \) равно \ (\ frac {1} {\ text {100}} \)

• \ (\ text {0,001} \) равно \ (\ frac {1} {\ text {1 000}} \)

Это означает, что

\ begin {align *} \ text {10,589} & = 10 + \ frac {5} {10} + \ frac {8} {100} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 000}} {\ text {1 000}} + \ frac {\ text {500}} {\ text {1 000}} + \ frac {80} {\ text {1 000 }} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 589}} {\ text {1 000}} \ end {выровнять *}

В следующих двух видеороликах объясняется, как преобразовать десятичные дроби в рациональные числа.

Часть 1

Видео: 2DBJ

Часть 2

Видео: 2DBK

Преобразование повторяющихся десятичных знаков в рациональные числа (EMA7)

Когда десятичная дробь является повторяющейся десятичной дробью, требуется немного больше работы, чтобы записать дробную часть десятичного числа в виде дроби.

Рабочий пример 2: Преобразование десятичных чисел в дроби

Запишите \ (\ text {0,} \ dot {3} \) в форме \ (\ frac {a} {b} \) (где \ (a \) и \ (b \) — целые числа).

Определите уравнение

\ [\ text {Let} x = \ text {0,33333 …} \]

Умножить на \ (\ text {10} \) с обеих сторон

\ [10x = \ текст {3,33333 …} \]

Вычтем первое уравнение из второго

\ [9x = 3 \]

Упростить

\ [x = \ frac {3} {9} = \ frac {1} {3} \]

Рабочий пример 3: Преобразование десятичных чисел в дроби

Запишите \ (\ text {5,} \ dot {4} \ dot {3} \ dot {2} \) в виде рациональной дроби.

Определите уравнение

\ [x = \ текст {5,432432432 …} \]

Умножить на \ (\ text {1 000} \) с обеих сторон

\ [\ text {1 000} x = \ text {5 432,432432432 …} \]

Вычтем первое уравнение из второго

\ [\ text {999} x = \ text {5 427} \]

Упростить

\ [x = \ frac {\ text {5 427}} {\ text {999}} = \ frac {\ text {201}} {\ text {37}} = \ text {5} \ frac {\ text { 16}} {\ text {37}} \]

В первом примере десятичное число было умножено на \ (\ text {10} \), а во втором примере десятичное число было умножено на \ (\ text {1 000} \).Это связано с тем, что в первом примере повторялась только одна цифра (т. Е. \ (\ Text {3} \)), а во втором — повторялись три цифры (т. Е. \ (\ Text {432} \)).

В общем, если у вас повторяется одна цифра, умножьте ее на \ (\ text {10} \). Если у вас повторяются две цифры, умножьте их на \ (\ text {100} \). Если у вас повторяются три цифры, умножьте их на \ (\ text {1 000} \) и так далее.

Не все десятичные числа можно записать как рациональные числа. Почему? Иррациональные десятичные числа, например \ (\ sqrt {2} = \ text {1,4142135…} \) нельзя записать с целым числителем и знаменателем, потому что они не имеют шаблона повторяющихся цифр и не завершаются.

Вы справитесь! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.

Зарегистрируйтесь, чтобы улучшить свои оценки

Упражнение 1.1

Какое место на диаграмме занимает число \ (- \ frac {12} {3} \)?

Сначала упростите дробь: \ (- \ frac {12} {3} = -4 \)

\ (- \ text {4} \) является целым числом, поэтому оно попадает в набор \ (\ mathbb {Z} \).

В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?

1. Каждое целое число — натуральное число.
2. Каждое натуральное число — это целое число.
3. В целых числах нет десятичных знаков.

Тщательно обдумайте каждый вариант:

1. Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
2. Натуральные числа — это \ (\ left \ {1; 2; 3; \ ldots \ right \} \), а целые числа — это \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \ ) (круг \ (\ mathbb {N} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является натуральным числом, оно должно быть целым числом. Это правда.
3. Целые числа \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным.

Итак, верно только (ii).

Какое место на диаграмме занимает число \ (- \ frac {1} {2} \)?

\ (- \ frac {1} {2} \) находится в своей простейшей форме, поэтому его нет в \ (\ mathbb {N} \), \ (\ mathbb {N} _0 \) или \ (\ mathbb {Z} \).Он находится в пространстве между прямоугольником и \ (\ mathbb {Z} \).

В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?

1. Каждое целое число — натуральное число.
2. Каждое целое число является целым.
3. В целых числах нет десятичных знаков.

Тщательно обдумайте каждый вариант:

1. Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
2. Целые числа \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \), а целые числа — \ (\ left \ {0 ; 1; 2; 3; \ ldots \ right \} \) (круг \ (\ mathbb {Z} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является целым это должно быть целое число. Это правда.
3. Целые числа \ (\ left \ {0; 1; 2; 3; 4; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным .

Итак, верно только (ii).

\ (- \ sqrt {3} \)

\ (- \ sqrt {3} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.

\ (\ dfrac {0} {\ sqrt {2}} \)

\ (\ dfrac {0} {\ sqrt {2}} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.

\ (\ sqrt {-9} \)

\ (\ sqrt {-9} \) имеет знак минус под квадратным корнем, поэтому он не является действительным.

\ (\ dfrac {- \ sqrt {7}} {0} \)

\ (\ dfrac {- \ sqrt {7}} {0} \) имеет деление на ноль, поэтому не определено.

\ (- \ sqrt {-16} \)

\ (- \ sqrt {-16} \) имеет отрицательное число под квадратным корнем, поэтому оно не является действительным.

\ (\ sqrt {2} \)

\ (\ sqrt {2} \) не имеет минуса под квадратным корнем (минус находится вне корня), не делится на ноль, поэтому он действительный.

\ (- \ frac {1} {3} \) рационально. Дробь целых чисел — это рациональное число.

\ (\ text {0,651268962154862.7 \) является рациональным, целым, целым и натуральным числом. Его можно записать как целое число.

\ (\ пи + 3 \)

\ (\ pi \) иррационально. \ (\ text {3} \) рационально (это целое число).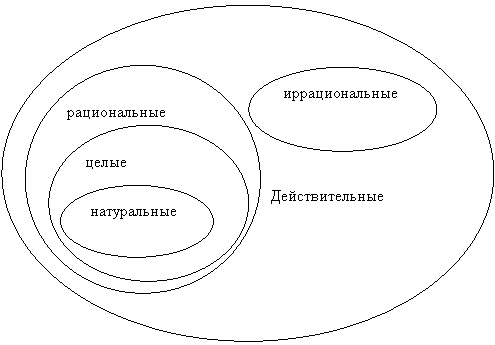 Любое рациональное число, добавленное к любому иррациональному числу, иррационально.

Следовательно, \ (\ pi + 3 \) иррационально.

\ (\ пи + \ текст {0,858408346} \)

\ (\ pi \) иррационально.\ (\ text {0,858408346} \) является рациональным (это конечная десятичная дробь). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.

Следовательно, \ (\ pi + \ text {0,858408346} \) иррационально.

\ (\ frac {5} {6} \) рационально.

Поскольку \ (a \) — целое число, \ (\ frac {a} {3} \) рационально.

Поскольку \ (b \) — целое число, \ (\ frac {-2} {b} \) рационально.

Обратите внимание, что \ (b \) не может быть \ (\ text {0} \), так как это делает дробь неопределенной.

Поскольку \ (c \) иррационально, \ (\ frac {1} {c} \) иррационально.

\ (\ frac {a} {14} = \ frac {1} {14} \) рационально.

\ (\ frac {a} {14} = \ frac {-10} {14} \) рационально.

\ (\ frac {a} {14} = \ frac {\ sqrt {2}} {14} \) иррационально.

\ (\ frac {a} {14} = \ frac {\ text {2,1}} {14} \) рационально.

Проверить, какое из чисел входит в набор \ (\ left \ {1; 2; 3; 4; \ ldots \ right \} \). Следовательно, \ (\ text {7} \) и \ (\ text {11} \) — натуральные числа.

Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- \ sqrt {8} \;; \; \ text {3,3231089 …} \;; \; 3+ \ sqrt {2} \;; \; \ pi \) все иррациональны.

Любое число, являющееся квадратным корнем из отрицательного числа, не является действительным.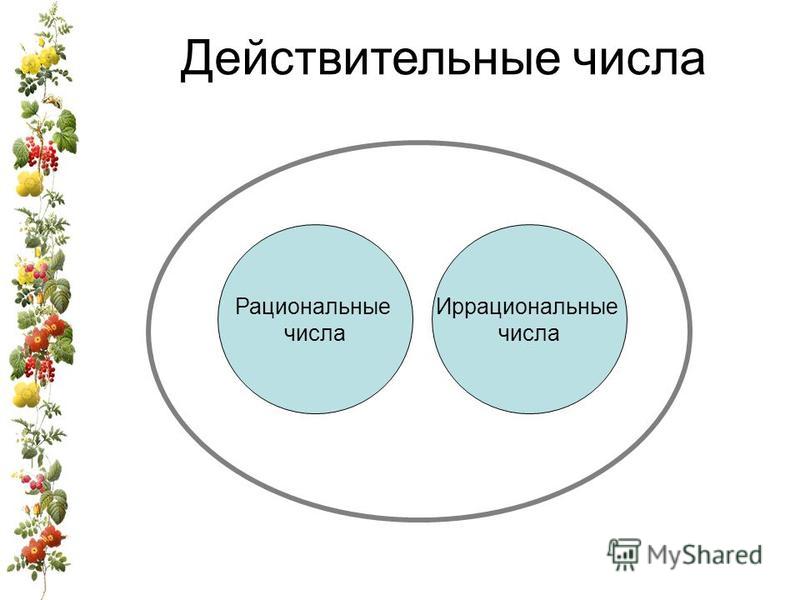 Следовательно, нереально только \ (\ sqrt {-1} \).

Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- 3 \;; \; 0 \;; \; -8 \ frac {4} {5} \;; \; \ frac {22} {7} \; \; 7 \;; \; \ text {1,} \ overline {34} \; \; 9 \ frac {7} {10} \;; \; 11 \) — все рациональные числа.

Проверьте, какое из чисел входит в набор \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \).Следовательно, \ (- 3 \;; \; 7 \;; \; 11 \) — целые числа.

Любая дробь, разделенная на \ (\ text {0} \), не определена. Следовательно, только \ (\ frac {14} {0} \) не определено.

\ (\ текст {2,121314 …} \)

• Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.

  Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.

• Нерационально, нет повторяющегося рисунка.

\ (\ текст {1,242244246 …} \)

• Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.

  Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.

• Нерационально, нет повторяющегося рисунка.

\ (\ текст {3,324354 …} \)

• Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.

  Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.

• Нерационально, нет повторяющегося рисунка.

\ (\ текст {3,3243} \ dot {5} \ dot {4} \)

\ (\ text {0,1} = \ frac {1} {10} \)

\ begin {align *} \ text {0,12} & = \ frac {1} {10} + \ frac {2} {100} \\ & = \ frac {10} {100} + \ frac {2} {100} \\ & = \ frac {12} {100} \\ & = \ frac {3} {25} \ end {выровнять *}

\ begin {align *} \ text {0,58} & = \ frac {5} {10} + \ frac {8} {100} \\ & = \ frac {50} {100} + \ frac {8} {100} \\ & = \ frac {58} {100} \\ & = \ frac {29} {50} \ end {выровнять *}

\ begin {align *} \ text {0,2589} & = \ frac {2} {10} + \ frac {5} {100} + \ frac {8} {\ text {1 000}} + \ frac {9} {\ text { 10 000}} \\ & = \ frac {\ text {2 000}} {\ text {10 000}} + \ frac {500} {\ text {10 000}} + \ frac {80} {\ text {10 000}} + \ гидроразрыв {9} {\ text {10 000}} \\ & = \ frac {\ text {2 589}} {\ text {10 000}} \ end {выровнять *}

Мы видим, что повторяется только цифра \ (\ text {1} \), поэтому мы можем записать это как \ (\ text {0,} \ dot {1} \).

\ (\ text {0,1212121212 …} \)

Существует повторяющийся образец \ (\ text {12} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {12} \)

\ (\ text {0,123123123123 …} \)

Существует повторяющийся шаблон \ (\ text {123} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {123} \)

\ (\ text {0,11414541454145 …} \)

Шаблон 4145 повторяется, поэтому мы можем записать это число как: \ (\ text {0,11} \ overline {4145} \).7 \ текст {00}} & = \ текст {2} \ текст {остаток} \ текст {4} \\ \ frac {\ text {7}} {\ text {33}} & = \ text {0,} \ text {2 121} \ ldots \\ & = \ текст {0,} \ точка {\ текст {2}} \ точка {\ текст {1}} \ end {выровнять *}

\ begin {align *} \ frac {2} {3} & = 2 \ left (\ frac {1} {3} \ right) \\ & = 2 (\ text {0,333333 . ..}) \\ & = \ текст {0,666666 …} \\ & = \ текст {0,} \ точка {6} \ end {выровнять *}

\ begin {align *} 1 \ frac {3} {11} & = 1 + 3 \ left (\ frac {1} {11} \ right) \\ & = 1 + 3 (\ text {0,0

…}) \\ & = 1 + \ текст {0,27272727 …} \\ & = \ текст {1,} \ overline {27} \ end {выровнять *}

\ begin {align *} 4 \ frac {5} {6} & = 4 + 5 \ left (\ frac {1} {6} \ right) \\ & = 4+ 5 (\ text {0,1666666 …}) \\ & = 4 + \ текст {0,833333 …} \\ & = \ текст {4,8} \ точка {3} \ end {выровнять *}

\ begin {align *} 2 \ frac {1} {9} & = 2 + \ text {0,1111111 …} \\ & = \ текст {2,} \ точка {1} \ end {выровнять *}

\ begin {align *} х & = \ текст {0,55555…} \ text {и} \\ 10x & = \ text {5,55555 .. .} \\ 10x — x & = (\ text {5,55555 …}) — (\ text {0,55555 …}) \\ \ text {9} x & = \ text {5} \\ \ поэтому x & = \ frac {5} {9} \ end {выровнять *}

\ begin {align *} 10x & = \ text {6,3333 …} \ text {и} \\ 100x & = \ текст {63,3333 …} \\ 100x — 10x & = (\ text {63,3333 …}) — (\ text {6,3333 …}) \\ \ text {99} x & = \ text {57} \\ \ поэтому x & = \ frac {57} {90} \ end {выровнять *}

\ (\ текст {0,} \ точка {4} \)

\ begin {align *} х & = \ текст {0,4444…} \ text {и} \\ \ text {10} x & = \ text {4,4444 …} \\ 10x — x & = (\ text {4,4444 …}) — (\ text {0,4444 …}) \\ \ text {9} x & = \ text {4} \\ \ поэтому x & = \ frac {\ text {4}} {\ text {9}} \ end {выровнять *}

\ (\ text {5,} \ overline {31} \)

\ begin {align *} х & = \ текст {5,313131 . ..} \ текст {и} \\ 100x & = \ text {531,313131 …} \\ 100x — x & = (\ text {531,313131…}) — (\ text {5,313131 …}) \\ \ text {99} x & = \ text {526} \\ \ поэтому x & = \ frac {526} {99} \ end {выровнять *}

\ (\ text {4,} \ overline {\ text {93}} \)

\ begin {align *} х & = \ текст {4,939393 …} \ текст {и} \\ 100x & = \ text {493,939393 …} \\ 100x — x & = (\ text {493,939393 …}) — (\ text {4,939393 …}) \\ \ text {99} x & = \ text {489} \\ \ поэтому x & = \ frac {\ text {163}} {\ text {33}} \ end {выровнять *}

\ (\ text {3,} \ overline {\ text {93}} \)

\ begin {align *} х & = \ текст {3,939393…} \ text {и} \\ 100x & = \ text {393,939393 …} \\ 100x — x & = (\ text {393,939393 …}) — (\ text {3,939393 …}) \\ \ text {99} x & = \ text {390} \\ \ поэтому x & = \ frac {\ text {130}} {\ text {33}} \ end {выровнять *}

Примеры уравнений с рациональными и иррациональными числами

Как рациональные, так и иррациональные числа можно назвать действительными числами, но когда дело доходит до их свойств, есть несколько отличий. Вы можете представить рациональное число в форме P / Q, где P и Q — целые числа, а Q 0.

Иррациональные числа нельзя записать простыми дробями. 2/3 — это пример рационального числа, тогда как √2 — иррациональное число.

Определения

Давайте начнем с определения каждого термина отдельно, затем мы сможем узнать больше о каждом и проработать несколько примеров.

Что такое рациональное число?

Любое число, выраженное в виде дроби с положительными, отрицательными числами и нулем, называется рациональным числом.Рациональные числа происходят от слова «соотношение». Другими словами, это соотношение двух целых чисел. Например, 3/2 — рациональное число, что означает деление 3 на другое целое число 2.

Что такое иррациональное число?

По сути, иррациональные числа могут быть записаны как десятичные дроби, но как отношение двух целых чисел. В иррациональных числах после десятичной точки обычно есть бесконечные неповторяющиеся цифры. Возьмем этот пример: √8 = 2,828.

Примеры рациональных и иррациональных чисел

Для Rational

• 0.5 можно записать как ½ или 5/10, а любое завершающее десятичное число является рациональным числом.
• √81 как квадратный корень можно упростить до 9, которое является частным от дроби 9/1
• Вы можете выразить 3 как 3/1, где 3 является частным целых чисел 3 и 1.
• 0,777777 — повторяющееся десятичное число и является рациональным числом.
• 1/5 — рациональное число, поскольку знаменатель и числитель являются целыми числами.

Для иррациональных значений

• √2 это число не может быть упрощено; следовательно, это иррациональное число.
• Π — это иррациональное число, имеющее значение 3,142…, которое является бесконечным и неповторяющимся числом. Следовательно, значение π не равно какой-либо дроби. Дробь 22/7 — это всего лишь оценка.
• 0,212112111… является иррациональным числом, которое не повторяется и не заканчивается, поэтому его нельзя выразить как частное от дроби.
• Хотя число в √7 / 5 дано как дробь, числитель и знаменатель должны быть целыми числами. Но поскольку √ 7 не является целым числом, указанное число иррационально.
• 5/0 иррационально. Любая дробь со знаменателем 0 иррациональна.

Свойства рациональных и иррациональных чисел

Это основные правила арифметики, выполняемые над рациональными и иррациональными числами

Правило 1: Результат суммы двух рациональных чисел также является рациональным

Правило 2: Произведение двух рациональных чисел является рациональным

Правило 3: результат суммы двух иррациональных чисел может быть рациональным или иррациональным

• Возьмем для примера: √2 + √2 = 2√2 иррационально
• , а 2 + 2√5 + (-2√5) = 2 результат является рациональным

Правило 4: Результат произведения двух иррациональных чисел может быть иррациональным или рациональным.

• Возьмем для примера: √2 * √3 = √6 иррационально
• , а √2 * √2 = √4 = 2 рациональных

Давайте теперь сосредоточимся на индивидуальных свойствах рациональных и иррациональных чисел.

Отличительные особенности рациональных чисел

• Сумма рациональных чисел всегда является рациональным числом. Например, если W и Z — два рациональных числа, сумма W и Z рациональна.
• Результат деления рационального числа на ненулевое число — рациональное число.Например, W ÷ Z = рациональное число.
• Произведение любых двух или трех рациональных чисел дает другое рациональное число. Например, если вы умножите W и Z, полученный ответ должен быть рациональным.
• Разница между двумя рациональными числами дает другое число. Например, если вы вычтете Z из W, вы получите рациональное число.

Поскольку результат суммы любых двух рациональных чисел является рациональным числом, рациональные числа всегда должны быть замкнутыми.Следовательно, рациональные числа одинаково закрыты для умножения, вычитания и деления, если делитель не равен нулю.

Как представить рациональные числа в виде десятичных знаков

Любое рациональное число можно выразить как завершающее десятичное или непрерывное десятичное число. Завершающий десятичный разделитель — это любое десятичное число, в котором после конечного числа десятичных знаков другие последующие значения разряда равны 0. Например, 1/8 = 0,125.

Как видно из данного примера, деление точное.Такие частные называются завершающими десятичными знаками. В качестве альтернативы, рациональные числа также могут быть выражены как непрерывные десятичные дроби. Неограничивающая десятичная дробь — это те десятичные дроби, которые бесконечно продолжаются после десятичной точки.

Давайте посмотрим на эти примеры:

1. 3/7 = 0,42857142
2. 18/23 = 0,78260869

В двух приведенных выше примерах вы понимаете, что разделение никогда не заканчивается, независимо от того, как долго оно может продолжаться. Частные таких делений называются завершающими десятичными знаками.

В некоторых случаях непрерывная десятичная дробь может иметь цифру или набор чисел, которые непрерывно повторяются. Эти непрерывные десятичные дроби называются периодическими, повторяющимися или циркулирующими десятичными знаками. Набор повторяющихся цифр называется периодом повторяющейся десятичной дроби.

Примеры

4/9 = 0,44444444

11/30 = 0,36666666

Отличительные особенности иррациональных чисел

• Произведение иррациональных чисел может быть как рациональным, так и иррациональным.
• Результат произведения ненулевого рационального числа и иррационального числа всегда иррационально.
• Сумма иррациональных чисел может быть как рациональной, так и иррациональной.
• Сумма рационального и иррационального числа всегда иррациональна.
• Разница между двумя иррациональными числами может быть или не быть иррациональной.
• Сумма рационального и иррационального числа всегда иррациональна.

Значительные различия между рациональными и иррациональными числами

• Рациональное число может быть выражено как отношение двух чисел в (форме p / q), а иррациональное число — нет.
• Рациональное число включает числа, которые могут заканчиваться или повторяться, в то время как иррациональные числа не завершаются и не повторяются.
• Рациональное число имеет полные квадраты, такие как 4, 9, 16, 25 и т. Д., В то время как иррациональные числа имеют морщины, такие как √2, √3, √5, √7.
• Для рационального числа числитель и знаменатель являются целыми числами, знаменатель которых не равен нулю: 3/2 = 1,5, 3,6767,
.
• Иррациональные числа нельзя записать дробью: √5, √11.

Часто задаваемые вопросы (FAQ)

Что такое рациональные и иррациональные числа?

Вы можете выразить рациональные числа в форме отношения (P / Q & Q ≠ 0), но для иррациональных чисел вы не можете выразить их в виде дроби.Тем не менее, оба они являются действительными числами, которые можно включить в числовую строку.

В чем существенная разница между рациональными и иррациональными числами?

Рациональные числа — это конечные и повторяющиеся десятичные дроби, а иррациональные числа — бесконечные и неповторяющиеся.

Пи — действительное число?

Пи (π) — иррациональное число, поэтому это действительное число.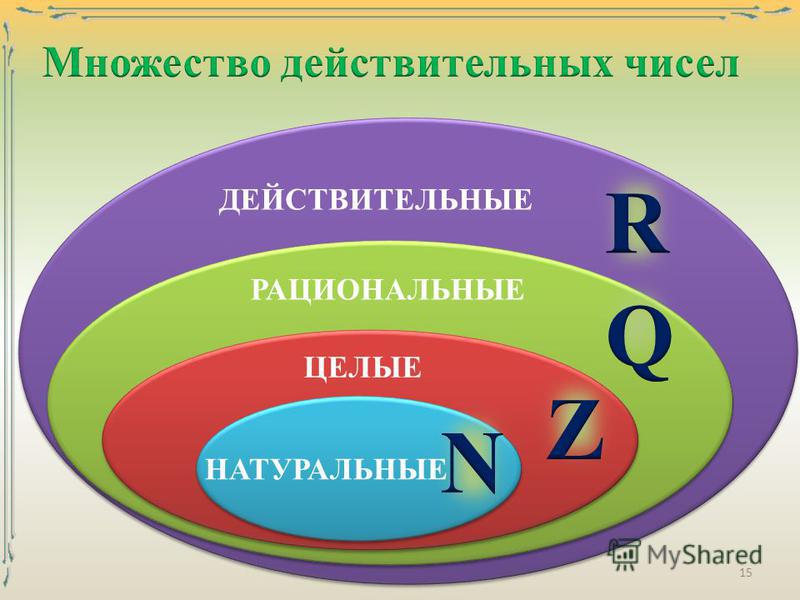 Значение (π) составляет 22/7 r 3,142…

Является ли 4 рациональным числом?

Да, это так, потому что оно удовлетворяет всем условиям рационального числа.Вы можете выразить это как отношение, если знаменатель не равен нулю.

Если вы представляете десятичное число чертой, оно рационально или иррационально? Десятичное число с полосой означает, что число после десятичной дроби повторяется, поэтому это рациональное число.

3.605551275… рационально или иррационально?

Многоточие (…) после 3.605551275 показывает, что число не завершается и не имеет повторяющегося шаблона. Так что это иррационально.

Заключение

Рациональные числа могут применяться для расчета скорости износа, колебаний, течения воды или скорости ветра.Приведенные выше примеры и объяснения позволяют любому легко отличить рациональное число от иррационального.

Оставьте первый комментарий ниже.

7.1: Рациональные и иррациональные числа

Поздравляем! Вы прочитали первые шесть глав этой книги! Пришло время подвести итоги того, что вы уже сделали в этом курсе, и подумать о том, что вас ждет впереди. Вы научились складывать, вычитать, умножать и делить целые числа, дроби, целые числа и десятичные дроби.Вы познакомились с языком и символами алгебры, а также упростили и оценили алгебраические выражения. Вы решили много разных типов приложений. Вы заложили хорошую прочную основу, необходимую для достижения успеха в алгебре.

В этой главе мы убедимся, что ваши навыки твердо закреплены. Мы еще раз взглянем на типы чисел, с которыми мы работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа.И мы попрактикуемся в их использовании, как при решении уравнений и выполнении других процедур в алгебре.

Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?

Рациональные числа

Какой тип чисел вы получите, если начнете со всех целых чисел, а затем включите все дроби? Числа, которые у вас получились бы, составили набор рациональных чисел.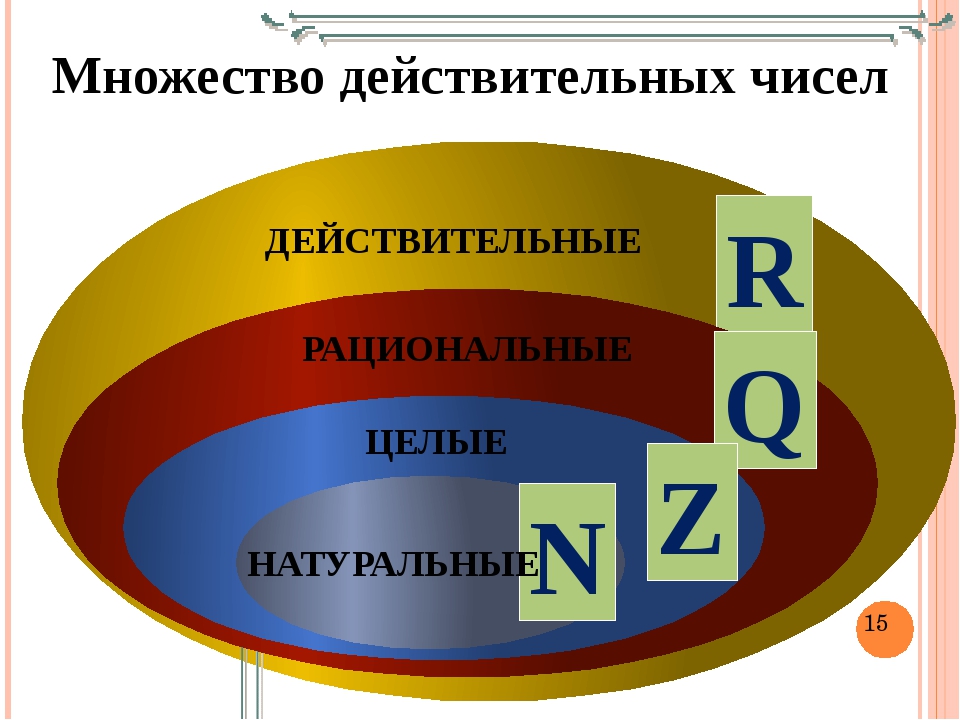 Рациональное число — это число, которое можно записать как отношение двух целых чисел.

Определение: рациональные числа

Рациональное число — это число, которое можно записать в форме \ (\ dfrac {p} {q} \), где p и q — целые числа, а q ≠ 0.

Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров:

\ [\ dfrac {4} {5}, — \ dfrac {7} {8}, \ dfrac {13} {4}, \; и\; — \ dfrac {20} {3} \]

Каждый числитель и каждый знаменатель — целое число.

Нам нужно посмотреть на все числа, которые мы использовали до сих пор, и убедиться, что они рациональны.Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.

Целые числа являются рациональными числами? Чтобы решить, является ли целое число рациональным числом, мы пытаемся записать его как отношение двух целых чисел. Легкий способ сделать это — записать дробь со знаминателем один.

\ [3 = \ dfrac {3} {1} \ quad -8 = \ dfrac {-8} {1} \ quad 0 = \ dfrac {0} {1} \]

Поскольку любое целое число можно записать как отношение двух целых чисел, все целые числа являются рациональными числами.Помните, что все счетные числа и все целые числа также являются целыми числами, а значит, они тоже рациональны.

А как насчет десятичных знаков? Они рациональны? Давайте посмотрим на несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа — это рациональные числа. Целое число -8 можно записать как десятичное -8,0. Итак, очевидно, что некоторые десятичные дроби рациональны.

Подумайте о десятичной системе счисления 7.3. Можем ли мы записать это как отношение двух целых чисел? Потому что 7.3 означает \ (7 \ dfrac {3} {10} \), мы можем записать его как неправильную дробь, \ (7 \ dfrac {3} {10} \). Итак, 7,3 — это соотношение целых чисел 73 и 10. Это рациональное число.

В общем, любое десятичное число, которое заканчивается рядом цифр (например, 7,3 или -1,2684), является рациональным числом. Мы можем использовать обратное (или мультипликативное обратное) значение разряда последней цифры в качестве знаменателя при записи десятичной дроби как дроби.

Пример \ (\ PageIndex {1} \):

Запишите каждое как отношение двух целых чисел: (a) −15 (b) 6.81 (c) \ (- 3 \ dfrac {6} {7} \).

Раствор

(а) −15

Запишите целое число в виде дроби со знаминателем 1.

$$ \ dfrac {-15} {1} $$

(б) 6.81

Запишите десятичную дробь как смешанное число.	$$ 6 \ dfrac {81} {100} $$
Затем преобразовать его в неправильную дробь.	$$ \ dfrac {681} {100} $$

(c) \ (- 3 \ dfrac {6} {7} \)

Преобразует смешанное число в неправильную дробь.

$$ — \ dfrac {27} {7} $$

Упражнение \ (\ PageIndex {1} \):

Запишите каждое как отношение двух целых чисел: (a) −24 (b) 3,57.

Ответить

\ (\ frac {-24} {1} \)

Ответ б

\ (\ frac {357} {100} \)

Упражнение \ (\ PageIndex {2} \):

Запишите каждое как отношение двух целых чисел: (a) −19 (b) 8.41.

Ответить

\ (\ frac {-19} {1} \)

Ответ б

\ (\ frac {841} {100} \)

Давайте посмотрим на десятичную форму чисел, которые, как мы знаем, рациональны. Мы видели, что каждое целое число является рациональным числом, поскольку a = \ (\ dfrac {a} {1} \) для любого целого числа, a. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.

\ [\ begin {split} Integer \ qquad & -2, \ quad -1, \ quad 0, \ quad 1, \; \; 2, \; 3 \\ Десятичный \ qquad & -2.0, -1.0, 0.0, 1.0, 2.0, 3.0 \ end {split} \]

Эти десятичные числа останавливаются.

Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму только что рассмотренных дробей.

\ [\ begin {split} Коэффициент \; из\; Целые числа \ qquad \ dfrac {4} {5}, \ quad — \ dfrac {7} {8}, \ quad \ dfrac {13} {4}, \; & — \ dfrac {20} {3} \\ Decimal \; формы \ qquad 0.8, -0.875, 3.25, & -6.666 \ ldots \\ & -6. \ overline {66} \ end {split} \]

Эти десятичные дроби либо останавливаются, либо повторяются.

Что вам говорят эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассматривали, выраженные как отношение целых чисел и десятичной дроби.

Рациональные числа
	Фракции	Целые числа
Номер	$$ \ dfrac {4} {5}, — \ dfrac {7} {8}, \ dfrac {13} {4}, \ dfrac {-20} {3} $$	$$ — 2, -1, 0, 1, 2, 3 $$
Коэффициент целого числа	$$ \ dfrac {4} {5}, \ dfrac {-7} {8}, \ dfrac {13} {4}, \ dfrac {-20} {3} $$	$$ \ dfrac {-2} {1}, \ dfrac {-1} {1}, \ dfrac {0} {1}, \ dfrac {1} {1}, \ dfrac {2} {1}, \ dfrac {3} {1} $$
Десятичное число	$$ 0.8, -0,875, 3,25, -6. \ Overline {6} $$	$$ — 2,0, -1,0, 0,0, 1,0, 2,0, 3,0 $$

Иррациональные числа

Есть ли десятичные дроби, которые не останавливаются и не повторяются? Да. Число \ (\ pi \) (греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не останавливается и не повторяется.

\ [\ pi = 3,141592654 \ ldots \ ldots \]

Точно так же десятичные представления квадратных корней из целых чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются.Например,

\ [\ sqrt {5} = 2.236067978 \ ldots \ ldots \]

Десятичная дробь, которая не останавливается и не повторяется, не может быть записана как отношение целых чисел. Мы называем такое число иррациональным числом .

Определение: иррациональное число

Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не останавливается и не повторяется.

Давайте резюмируем метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.

Если десятичная форма числа

• остановок или повторений, количество рациональное.
• не останавливается и не повторяется, цифра иррациональна.

Пример \ (\ PageIndex {2} \):

Определите каждое из следующего как рациональное или иррациональное: (a) 0,58 \ (\ overline {3} \) (b) 0,475 (c) 3,605551275…

Раствор

(а) 0,58 \ (\ overline {3} \)

Полоса над цифрой 3 указывает на то, что это повторяется.Следовательно, 0,583 — это повторяющееся десятичное число, а значит, является рациональным числом.

(б) 0,475

Эта десятичная дробь заканчивается после 5, так что это рациональное число.

(в) 3.605551275…

Многоточие (…) означает, что это число не останавливается. Нет повторяющегося рисунка цифр. Поскольку число не останавливается и не повторяется, это нерационально.

Упражнение \ (\ PageIndex {3} \):

Определите каждое из следующего как рациональное или иррациональное: (a) 0.29 (б) 0,81 \ (\ overline {6} \) (в) 2,515115111…

Ответить

рациональный

Ответ б

рациональный

Ответ c

иррационально

Упражнение \ (\ PageIndex {4} \):

Определите каждое из следующего как рациональное или иррациональное: (a) 0,2 \ (\ overline {3} \) (b) 0,125 (c) 0,418302…

Ответить

рациональный

Ответ б

рациональный

Ответ c

иррационально

Давайте теперь подумаем о квадратных корнях.Квадратные корни из полных квадратов всегда целые числа, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.

Пример \ (\ PageIndex {3} \):

Определите каждое из следующих действий как рациональное или иррациональное: (a) 36 (b) 44

Раствор

(a) Число 36 — это полный квадрат, так как 6 ² = 36. Итак, \ (\ sqrt {36} \) = 6. Следовательно, \ (\ sqrt {36} \) рационально.

(b) Помните, что 6 ² = 36 и 7 ² = 49, поэтому 44 не является полным квадратом. Это означает, что \ (\ sqrt {44} \) иррационально.

Упражнение \ (\ PageIndex {5} \):

Определите каждое из следующего как рациональное или иррациональное: (a) \ (\ sqrt {81} \) (b) \ (\ sqrt {17} \)

Ответить

рациональный

Ответ б

иррационально

Упражнение \ (\ PageIndex {6} \):

Определите каждое из следующего как рациональное или иррациональное: (a) \ (\ sqrt {116} \) (b) \ (\ sqrt {121} \)

Ответить

иррационально

Ответ б

рациональный

Рациональные и иррациональные числа — Surds — Higher — CCEA — GCSE Maths Revision — CCEA

Число считается рациональным, если его можно записать в виде дроби (одно целое число, деленное на другое целое число).Десятичная форма рационального числа имеет либо завершающую, либо повторяющуюся десятичную дробь. Примеры рациональных чисел: 17, -3 и 12.4. Другие примеры рациональных чисел: ⁵ ⁄ ₄ = 1,25 (завершающее десятичное число) и ² ⁄ ₃ = \ (0. \ Dot {6} \) (повторяющееся десятичное число).

Число иррационально, если его нельзя записать в виде дроби. Десятичная форма иррационального числа не прерывается и не повторяется. Примеры иррациональных чисел: \ (π \) = 3.14159 … и \ (\ sqrt {2} = 1.414213 \ dotsc \)

Surds

Surd — это выражение, которое включает квадратный корень, кубический корень или другой символ корня. Сурды используются для точной записи иррациональных чисел — поскольку десятичные дроби в иррациональных числах не заканчиваются и не повторяются, они не могут быть записаны точно в десятичной форме.

Пример

Площадь этого квадрата 3 м ² . Рассчитайте длину каждой стороны.

Длина каждой стороны равна \ (\ sqrt {3} \).2 \) дает 2,9929 м ² .

Ответ в форме surd дает нам возможность записать точный ответ, что полезно, если мы хотим использовать это значение в дальнейших вычислениях, чтобы минимизировать ошибки округления. Ответ в десятичной форме дает нам приблизительный ответ, который полезен, если мы хотим использовать ответ в практических целях, например, для рисования квадрата.

Рациональные и иррациональные числа Видео

Не будьте такими иррациональными, числа.

00:18

<> Для вечеринки по случаю вручения кинопремии у меня есть шесть желатиновых форм [номер шесть, говорящий по мобильному телефону]

00:24

с изображением лица Бена Аффлека.

00:25

Но у меня восемь гостей.

00:27

Можно ли разделить их поровну?

00:30

Это рационально?

00:31

Спасибо за вопрос, вызывающий 1.

00:33

Хотя каждый гость не получит целую голову Аффлека, они могут получить часть одной. [6 желатиновых головок Аффлека на доске]

00:38

Поскольку у вас шесть форм, вы разделите это число на количество гостей — восемь.

00:44

Шесть, разделенная на восемь, совпадает с дробью шесть восьмых.

00:47

Таким образом, каждый гость получит шесть восьмых Аффлека… которые можно уменьшить до трех четвертей.

00:52

Это может быть не целое число, но это рациональное число: число, которое можно записать [Число 3, слушая ответ по телефону]

00:56

как частное двух целых чисел.

00:59

Следующий абонент, вы в эфире.

01:00

Я действительно хочу челку, как у первой леди. [Число 6 в кресле-качалке]

01:04

Мне пришлось бы отрастить волосы еще на три дюйма.

01:07

Это рационально?

01:09

Да, три — это целое число и целое число.

01:11

Это вполне рационально.[5 показывает ответ]

01:13

Хорошо, но мой парикмахер хочет взимать с меня «квадратный корень из двух» [Номер 6 делает прическу]

01:19

долларов за стрижка.

01:22

Я даже не знаю, сделка это или нет.

01:24

Это рационально?

01:25

Мы рады, что вы спросили вызывающего 2.

01:27

Не существует рационального числа, которое при умножении на само себя дает ответ 2.

01:32

Не существует реального эквивалента квадратного корня из двух.

01:35

Итак, нет…

01:36

Это число иррационально… что означает, что, возможно, вам пора найти нового стилиста.

01:41

Настройтесь в следующий раз, когда мы поговорим о том, что вести жизнь Пи было бы иррационально… [Появляется мысленный пузырь Жизни Пи]

01:45

… но деление трех пироги на четверых были бы вполне рациональными.[4 человека за столом с 3 пирогами]

Определение иррационального числа

Домашняя страница: Технические термины: Определение иррационального числа

Иррациональное число — это действительное число, которое не может быть выражено как отношение двух целых чисел. Когда иррациональное число записывается с десятичной точкой, числа после десятичной точки продолжаются бесконечно без повторяющегося образца.

Число «пи» или π (3,14159 …) является распространенным примером иррационального числа, поскольку оно имеет бесконечное количество цифр после десятичной точки.Многие квадратные корни также иррациональны, поскольку их нельзя свести к дробям. Например, √2 близко к 1,414, но точное значение не определено, поскольку цифры после десятичной точки продолжаются бесконечно: 1,414213562373095 … Это значение не может быть выражено в виде дроби, поэтому квадратный корень из 2 является иррациональным.

По состоянию на 2018 год, число π составляло 22 триллиона цифр, и никаких закономерностей обнаружено не было.

Если число может быть выражено как отношение двух целых чисел, оно является рациональным.Ниже приведены несколько примеров иррациональных и рациональных чисел.

• 2 — рациональный
• √2 — иррациональный
• 3,14 — рациональное
• π — иррациональное
• √3 — иррациональный
• √4 — рациональный
• 7/8 — рациональное
• 1,333 (повторение) — рациональное
• 1,567 (повторение) — рациональное
• 1.567183906 (не повторяется) — иррационально

ПРИМЕЧАНИЕ: Когда компьютерная программа встречает иррациональные числа, они должны быть оценены.

Обновлено: 5 июня 2018 г.

https://techterms.com/definition/irrational_number

TechTerms — Компьютерный словарь технических терминов

Эта страница содержит техническое определение иррационального числа. Он объясняет в компьютерной терминологии, что означает иррациональное число, и является одним из многих технических терминов в словаре TechTerms.

Все определения на веб-сайте TechTerms составлены так, чтобы быть технически точными, но также простыми для понимания. Если вы найдете это определение иррационального числа полезным, вы можете сослаться на него, используя приведенные выше ссылки для цитирования.Если вы считаете, что термин следует обновить или добавить в словарь TechTerms, отправьте электронное письмо в TechTerms!

Подпишитесь на информационный бюллетень TechTerms, чтобы получать избранные термины и тесты прямо в свой почтовый ящик.