Нейронные сети для начинающих. Часть 1 / Habr

Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.
Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат.
Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:
| a | b | c |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Что такое нейронная сеть?
Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.
Какие бывают нейронные сети?
Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.
Для чего нужны нейронные сети?
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.
Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.
Что такое нейрон?
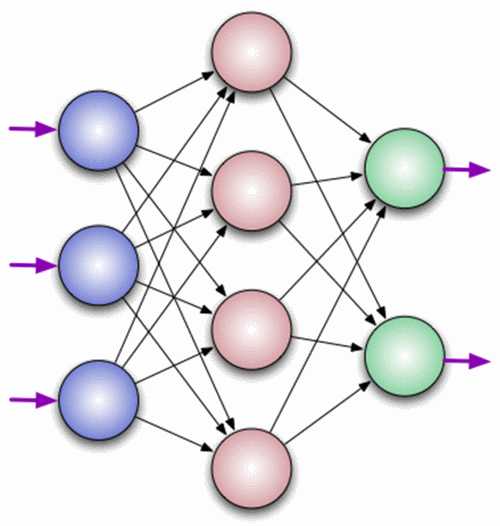
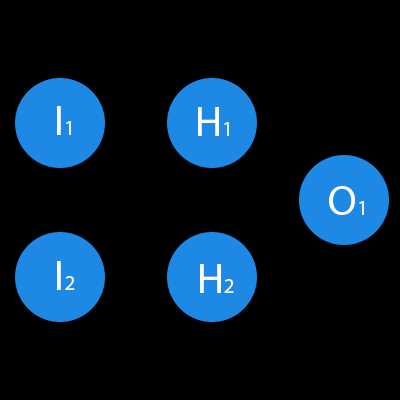
Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.
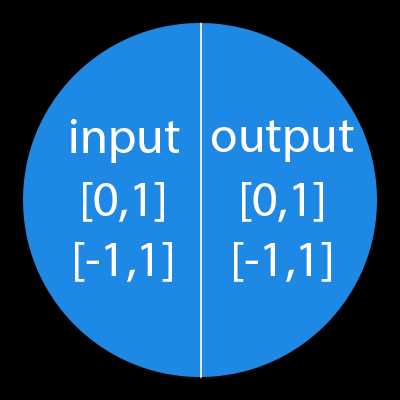
Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.
Что такое синапс?
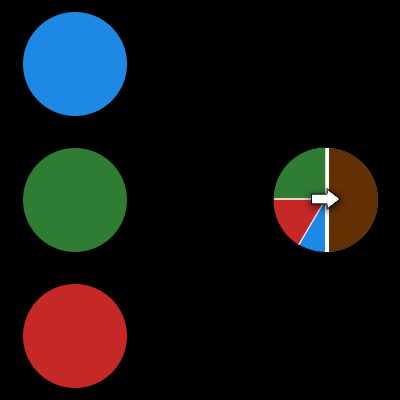
Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Как работает нейронная сеть?
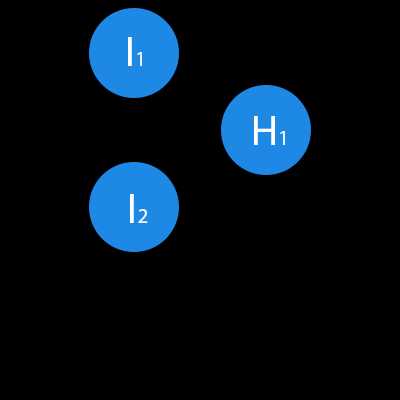
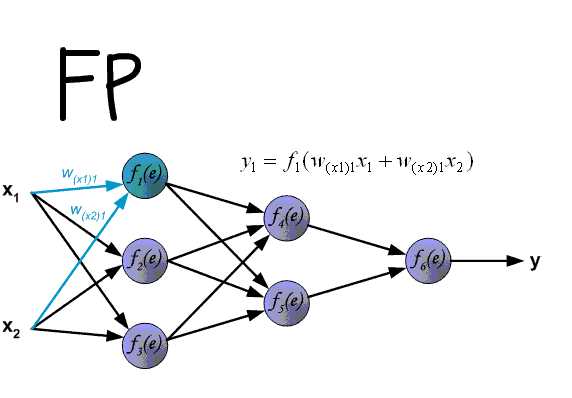
В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.
Функция активации
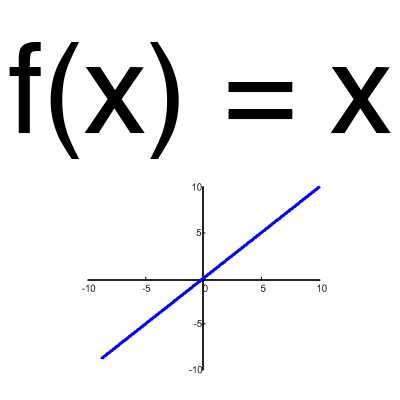
Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.
Сигмоид
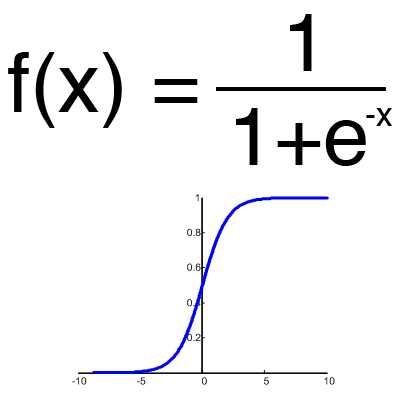
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.
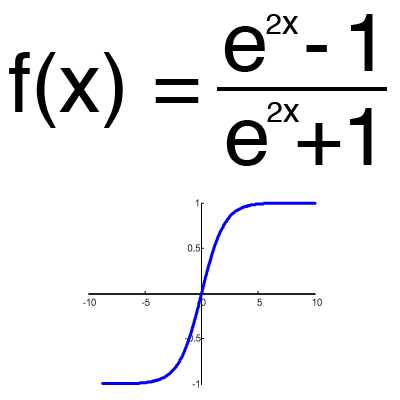
Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.
Тренировочный сет
Итерация
Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.
Эпоха
При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.
раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.
Ошибка
Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.
MSE
Root MSE
Arctan
Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.
Задача
Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
Решениеh2input = 1*0.45+0*-0.12=0.45
h2output = sigmoid(0.45)=0.61
h3input = 1*0.78+0*0.13=0.78
h3output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.
Использованные ресурсы:
— Раз
— Два
— Три
habr.com
Искусственная нейронная сеть — Википедия
Схема простой нейросети. Зелёным цветом обозначены входные нейроны, голубым — скрытые нейроны, жёлтым — выходной нейронИску́сственная нейро́нная се́ть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети У. Маккалока и У. Питтса[1]. После разработки алгоритмов обучения получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
ИНС представляет собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Такие процессоры обычно довольно просты (особенно в сравнении с процессорами, используемыми в персональных компьютерах). Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И, тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие по отдельности простые процессоры вместе способны выполнять довольно сложные задачи.
Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что в случае успешного обучения сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке, а также неполных и/или «зашумленных», частично искажённых данных.
- 1943 — У. Маккалок и У. Питтс формализуют понятие нейронной сети в фундаментальной статье о логическом исчислении идей и нервной активности[1]. В начале своего сотрудничества с Питтсом Н. Винер предлагает ему вакуумные лампы в качестве идеального на тот момент средства для реализации эквивалентов нейронных сетей[3].
- 1948 — опубликована книга Н. Винера о кибернетике. Основной идеей является представление сложных биологических процессов математическими моделями.
- 1949 — Д. Хебб предлагает первый алгоритм обучения.
- В 1958 Ф. Розенблатт изобретает однослойный перцептрон и демонстрирует его способность решать задачи классификации[4]. Перцептрон обрёл популярность — его используют для распознавания образов, прогнозирования погоды и т. д.; в то время казалось, что уже не за горами создание полноценного искусственного интеллекта. К моменту изобретения перцептрона завершилось расхождение теоретических работ Маккалока с т. н. «кибернетикой» Винера; Маккалок и его последователи вышли из состава «Кибернетического клуба».
- В 1960 году Бернард Уидроу[en] совместно со своим студентом Хоффом на основе дельта-правила (формулы Уидроу) разработали Адалин, который сразу начал использоваться для задач предсказания и адаптивного управления. Адалин был построен на базе созданных ими же (Уидроу — Хоффом) принципиально новых элементах — мемисторах[5]. Сейчас Адалин (адаптивный сумматор) является стандартным элементом многих систем обработки сигналов[6].
- В 1963 году в Институте проблем передачи информации АН СССР. А. П. Петровым проводится подробное исследование задач «трудных» для перцептрона[7]. Эта пионерская работа в области моделирования ИНС в СССР послужила отправной точкой для комплекса идей М. М. Бонгарда — как «сравнительно небольшой переделкой алгоритма (перцептрона) исправить его недостатки»[8]. Работы А. П. Петрова и М. М. Бонгарда весьма способствовали тому, что в СССР первая волна эйфории по поводу ИНС была сглажена.
- В 1969 году М. Минский публикует формальное доказательство ограниченности перцептрона и показывает, что он неспособен решать некоторые задачи (проблема «чётности» и «один в блоке»), связанные с инвариантностью представлений. Интерес к нейронным сетям резко спадает.
- В 1972 году Т. Кохонен и Дж. Андерсон[en] независимо предлагают новый тип нейронных сетей, способных функционировать в качестве памяти[9].
- В 1973 году Б. В. Хакимов предлагает нелинейную модель с синапсами на основе сплайнов и внедряет её для решения задач в медицине, геологии, экологии[10].
- 1974 — Пол Дж. Вербос[11] и А. И. Галушкин[12] одновременно изобретают алгоритм обратного распространения ошибки для обучения многослойных перцептронов[13]. Изобретение не привлекло особого внимания.
- 1975 — Фукусима[en] представляет когнитрон — самоорганизующуюся сеть, предназначенную для инвариантного распознавания образов, но это достигается только при помощи запоминания практически всех состояний образа.
- 1982 — после периода забвения, интерес к нейросетям вновь возрастает. Дж. Хопфилд показал, что нейронная сеть с обратными связями может представлять собой систему, минимизирующую энергию (так называемая сеть Хопфилда). Кохоненом представлены модели сети, обучающейся без учителя (нейронная сеть Кохонена), решающей задачи кластеризации, визуализации данных (самоорганизующаяся карта Кохонена) и другие задачи предварительного анализа данных.
- 1986 — Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[14] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[15] переоткрыт и существенно развит метод обратного распространения ошибки. Начался взрыв интереса к обучаемым нейронным сетям.
- 2007 — Джеффри Хинтоном в университете Торонто созданы алгоритмы глубокого обучения многослойных нейронных сетей. Успех обусловлен тем, что Хинтон при обучении нижних слоев сети использовал ограниченную машину Больцмана (RBM — Restricted Boltzmann Machine). Глубокое обучение по Хинтону — это очень медленный процесс. Необходимо использовать много примеров распознаваемых образов (например, множество лиц людей на разных фонах). После обучения получается готовое быстро работающее приложение, способное решать конкретную задачу (например, осуществлять поиск лиц на изображении). Функция поиска лиц людей на сегодняшний день стала стандартной и встроена во все современные цифровые фотоаппараты. Технология глубокого обучения активно используется интернет-поисковиками при классификации картинок по содержащимся в них образам. Применяемые при распознавании искусственные нейронные сети могут иметь до 9 слоёв нейронов, их обучение ведётся на миллионах изображений с отыскиваемым образом.
Распознавание образов и классификация[править | править код]
В качестве образов могут выступать различные по своей природе объекты: символы текста, изображения, образцы звуков и т. д. При обучении сети предлагаются различные образцы образов с указанием того, к какому классу они относятся. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно. По окончании обучения сети ей можно предъявлять неизвестные ранее образы и получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из её выходов должен появиться признак того, что образ принадлежит этому классу. В то же время на других выходах должен быть признак того, что образ данному классу не принадлежит[16]. Если на двух или более выходах есть признак принадлежности к классу, считается, что сеть «не уверена» в своём ответе.
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Обучение без учителя:
- Смешанное обучение:
Принятие решений и управление[править | править код]
Эта задача близка к задаче классификации. Классификации подлежат ситуации, характеристики которых поступают на вход нейронной сети. На выходе сети при этом должен появиться признак решения, которое она приняла. При этом в качестве входных сигналов используются различные критерии описания состояния управляемой системы[17].
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Смешанное обучение:
Кластеризация[править | править код]
Под кластеризацией понимается разбиение множества входных сигналов на классы, при том, что ни количество, ни признаки классов заранее не известны. После обучения такая сеть способна определять, к какому классу относится входной сигнал. Сеть также может сигнализировать о том, что входной сигнал не относится ни к одному из выделенных классов — это является признаком новых, отсутствующих в обучающей выборке, данных. Таким образом, подобная сеть может выявлять новые, неизвестные ранее классы сигналов. Соответствие между классами, выделенными сетью, и классами, существующими в предметной области, устанавливается человеком. Кластеризацию осуществляют, например, нейронные сети Кохонена.
Нейронные сети в простом варианте Кохонена не могут быть огромными, поэтому их делят на гиперслои (гиперколонки) и ядра (микроколонки). Если сравнивать с мозгом человека, то идеальное количество параллельных слоёв не должно быть более 112. Эти слои в свою очередь составляют гиперслои (гиперколонку), в которой от 500 до 2000 микроколонок (ядер). При этом каждый слой делится на множество гиперколонок, пронизывающих насквозь эти слои. Микроколонки кодируются цифрами и единицами с получением результата на выходе. Если требуется, то лишние слои и нейроны удаляются или добавляются. Идеально для подбора числа нейронов и слоёв использовать суперкомпьютер. Такая система позволяет нейронным сетям быть пластичными.
Используемые архитектуры нейросетей[править | править код]
- Обучение без учителя:
Прогнозирование[править | править код]
Способности нейронной сети к прогнозированию напрямую следуют из её способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и (или) каких-то существующих в настоящий момент факторов. Следует отметить, что прогнозирование возможно только тогда, когда предыдущие изменения действительно в какой-то степени предопределяют будущие. Например, прогнозирование котировок акций на основе котировок за прошлую неделю может оказаться успешным (а может и не оказаться), тогда как прогнозирование результатов завтрашней лотереи на основе данных за последние 50 лет почти наверняка не даст никаких результатов.
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Смешанное обучение:
Аппроксимация[править | править код]
Нейронные сети могут аппроксимировать непрерывные функции. Доказана обобщённая аппроксимационная теорема[18]: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любую непрерывную функцию с некоторой наперёд заданной точностью. Это означает, что нелинейная характеристика нейрона может быть произвольной: от сигмоидальной до произвольного волнового пакета или вейвлета, синуса или многочлена. От выбора нелинейной функции может зависеть сложность конкретной сети, но с любой нелинейностью сеть остаётся универсальным аппроксиматором и при правильном выборе структуры может достаточно точно аппроксимировать функционирование любого непрерывного автомата.
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Смешанное обучение:
Сжатие данных и ассоциативная память[править | править код]
Способность нейросетей к выявлению взаимосвязей между различными параметрами дает возможность выразить данные большой размерности более компактно, если данные тесно взаимосвязаны друг с другом. Обратный процесс — восстановление исходного набора данных из части информации — называется (авто)ассоциативной памятью. Ассоциативная память позволяет также восстанавливать исходный сигнал/образ из зашумленных/поврежденных входных данных. Решение задачи гетероассоциативной памяти позволяет реализовать память, адресуемую по содержимому[17].
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Обучение без учителя:
Анализ данных[править | править код]
Используемые архитектуры нейросетей[править | править код]
- Обучение с учителем:
- Обучение без учителя:
Оптимизация[править | править код]
Используемые архитектуры нейросетей[править | править код]
- Обучение без учителя:
- Сбор данных для обучения;
- Подготовка и нормализация данных;
- Выбор топологии сети;
- Экспериментальный подбор характеристик сети;
- Экспериментальный подбор параметров обучения;
- Собственно обучение;
- Проверка адекватности обучения;
- Корректировка параметров, окончательное обучение;
- Вербализация сети[19] с целью дальнейшего использования.
Следует рассмотреть подробнее некоторые из этих этапов.
Сбор данных для обучения[править | править код]
Выбор данных для обучения сети и их обработка является самым сложным этапом решения задачи. Набор данных для обучения должен удовлетворять нескольким критериям:
- Репрезентативность — данные должны иллюстрировать истинное положение вещей в предметной области;
- Непротиворечивость — противоречивые данные в обучающей выборке приведут к плохому качеству обучения сети.
Исходные данные преобразуются к виду, в котором их можно подать на входы сети. Каждая запись в файле данных называется обучающей парой или обучающим вектором. Обучающий вектор содержит по одному значению на каждый вход сети и, в зависимости от типа обучения (с учителем или без), по одному значению для каждого выхода сети. Обучение сети на «сыром» наборе, как правило, не даёт качественных результатов. Существует ряд способов улучшить «восприятие» сети.
- Нормировка выполняется, когда на различные входы подаются данные разной размерности. Например, на первый вход сети подаются величины со значениями от нуля до единицы, а на второй — от ста до тысячи. При отсутствии нормировки значения на второ
ru.wikipedia.org
Нейронные сети с нуля. Обзор курсов и статей на русском языке, бесплатно и без регистрации
На Хабре периодически появляются обзоры курсов по машинному обучению. Но такие статьи чаще добавляют в закладки, чем проходят сами курсы. Причины для этого разные: курсы на английском языке, требуют уверенного знания матана или специфичных фреймворков (либо наоборот не описаны начальные знания, необходимые для прохождения курса), находятся на других сайтах и требуют регистрации, имеют расписание, домашнюю работу и тяжело сочетаются с трудовыми буднями. Всё это мешает уже сейчас с нуля начать погружаться в мир машинного обучения со своей собственной скоростью, ровно до того уровня, который интересен и пропускать при этом неинтересные разделы.В этом обзоре в основном присутствуют только ссылки на статьи на хабре, а ссылки на другие ресурсы в качестве дополнения (информация на них на русском языке и не нужно регистрироваться). Все рекомендованные мною статьи и материалы я прочитал лично. Я попробовал каждый видеокурс, чтобы выбрать что понравится мне и помочь с выбором остальным. Большинство статей мною были прочитаны ранее, но есть и те на которые я наткнулся во время написания этого обзора.
Обзор состоит из нескольких разделов, чтобы каждый мог выбрать уровень с которого можно начать.
Для крупных разделов и видео-курсов указаны приблизительные временные затраты, необходимые знания, ожидаемые результаты и задания для самопроверки.
Большинство статей не было написано в рамках единого курса, поэтому информация может дублироваться. Если вы видите, что знаете какую-то часть статьи, то можете её смело пропустить, если вы не разорались с этой информацией в предыдущей статье, то у вас есть шанс прочитать тоже самое, но другими словами, что должно помочь усвоению материала.
Вводные статьи
Требуемый уровень: школьное образование, знание русского языка.
Требуемое время: несколько часов.
Казалось бы, что стоит начать изучение со статьи Искусственная нейронная сеть на википедии, но я не рекомендую. Наискучнейшее описание отбивает всё желание изучать нейронные сети.
Нейронки за 5 минут (слишком упрощённое описание, для гуманитариев, зато потребуется всего 5 минут)
Искусственные нейронные сети простыми словами (лучше потратить 15 минут на эту статью)
Основы ИНС (одна из четырёх статей из Учебник — Нейронные сети)
Нейронные сети для начинающих. Часть 1 и Часть 2
Нейронные сети, фундаментальные принципы работы, многообразие и топология
Искусственные нейронные сети и миниколонки реальной коры (девятая часть из курса Логика сознания)
Расширяем горизонты
Требуемый уровень: базовое понимание работы нейронных сетей.
Требуемое время: несколько часов.
Краткий курс машинного обучения или как создать нейронную сеть для решения скоринг задачи
Самое главное о нейронных сетях. Лекция в Яндексе (рекомендую посмотреть только видео на 1 час, читать статью показалось тяжеловато)
Введение в архитектуры нейронных сетей
Что такое свёрточная нейронная сеть
Свёрточная нейронная сеть, часть 1: структура, топология, функции активации и обучающее множество
Зоопарк архитектур нейронных сетей. Часть 1 и Часть 2 (Особо вчитываться не надо, достаточно посмотреть красивые картинки и прочитать описание по диагонали)
- типы задач, которые решают нейронные сети
- типы архитектур нейронных сетей
- функции активации
- типы нейронов / слоёв
Углубляем знания
Требуемый уровень: понимание работы нейронных сетей, знание базовых архитектур.
Требуемое время: несколько десятков часов.
Курс о Deep Learning на пальцах от АФТИ НГУ (14 видеороликов, 15 часов, будет познавательно)
Материалы открытого курса OpenDataScience и Mail.Ru Group по машинному обучению (10 видеороликов, 20 часов, будет сложно)
Лекции Техносферы. Нейронные сети в машинном обучении (14 видеороликов, 25 часов, будет скучно)
Чтобы определиться самому и помочь с выбором остальным хабровчанам, я построил график падения интереса к курсу на основе падения количества просмотров каждого следующего ролика. Выводы неутешительные — мало кто доходит до конца. Самый большой процент дошедших до конца — у курса от АФТИ НГУ.
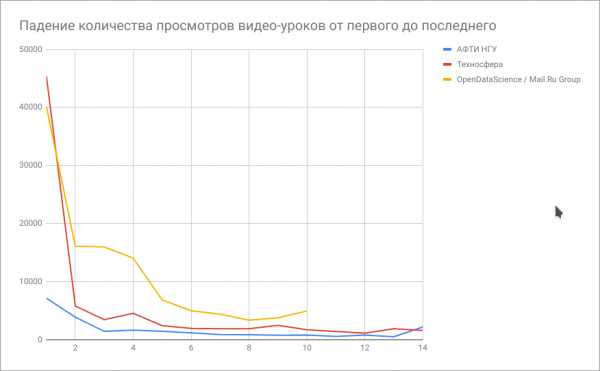
(График падения количества просмотров составлялся пару месяцев назад и текущая картина может немного отличаться).
Примеры применения на практике
Сюда вошли в основном только те статьи, после которых прочитавшие их люди смогут сами воспроизвести описанные результаты (есть ссылки на исходники или онлайн сервисы)
ТОП30 самых впечатляющих проектов по машинному обучению за прошедший год (v.2018)
Улучшение качества изображения с помощью нейронной сети
Детектирование частей тела с помощью глубоких нейронных сетей
Классификация объектов в режиме реального времени
Раскрашиваем чёрно-белую фотографию с помощью нейросети
Смена пола и расы на селфи с помощью нейросетей
Как различать британскую и американскую литературу с помощью машинного обучения
Разделение текста на предложения с помощью Томита-парсера
WaveNet: новая модель для генерации человеческой речи и музыки
Анализ Корана при помощи AI
Сколько нужно нейронов, чтобы узнать, разведён ли мост Александра Невского?
Сколько котов на хабре?
Торговля знает, когда вы ждете ребенка
Стэнфордская нейросеть определяет тональность текста с точностью 85%
Топливо для ИИ: подборка открытых датасетов для машинного обучения
Другие материалы
Статьи и курсы, которые не вошли в мой обзор, но возможно вам понравятся.
Нейронные сети в картинках: от одного нейрона до глубоких архитектур (python, numpy)
Базовые принципы машинного обучения на примере линейной регрессии (python, numpy, матан)
Сверточная нейронная сеть, часть 2: обучение алгоритмом обратного распространения ошибки (матан)
Нейронные сети на stepik.org (в обзоре двухлетней давности его уже тогда называли устаревшим)
Курс по машинному обучению на Coursera от Яндекса и ВШЭ (курс доступен только после регистрации, NumPy, Pandas, Scikit-Learn)
Deep Learning For Coders (7 видеороликов, 15 часов, английский язык)
Курс Deep Learning от Google на udacity (английский язык)
Курс Структурирование проектов по машинному обучению на Coursera (платный, английский язык)
Другие статьи-обзоры на хабре по изучению машинного обучения
Где и как изучать машинное обучение? (английский язык)
Что читать о нейросетях 10 книг (английский язык)
Обучаемся самостоятельно: подборка видеокурсов по Computer Science (английский язык)
Обзор курсов по Deep Learning (английский язык)
10 курсов по машинному обучению на лето (английский/русский язык, платно/бесплатно)
Прочтение этих статей и подтолкнуло меня написать свою собственную, в которой были бы материалы только на русском языке, без регистрации и требования 5 лет матана.
Надеюсь, что у моей статьи будет меньше комментариев вида:
«Закинул в закладки. Смотреть я их, конечно, не буду.»
Прошу всех заинтересованных лиц ответить на опросы после статьи, ну и подписывайтесь, чтобы не пропустить мои следующие статьи, ставьте лайки, чтобы мотивировать меня на их написание и пишите в комментариях вопросы (опечатки лучше в личку).
Традиционное предупреждение: я не отвечаю на сообщения в личку/соцсетях/телеграмме и т.д. Если у вас есть вопрос, то задавайте его в комментариях.
habr.com
Нейронные сети для начинающих. Часть 2 / Habr

Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
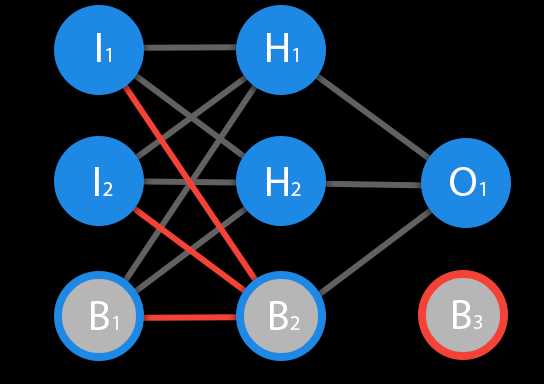
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
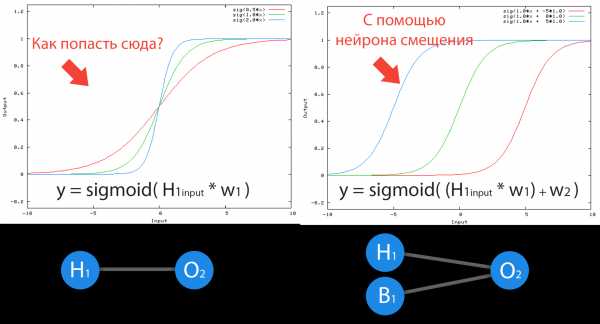
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу h2, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес h2, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = h2*w1+h3*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
- Метод обратного распространения (Backpropagation)
- Метод упругого распространения (Resilient propagation или Rprop)
- Генетический Алгоритм (Genetic Algorithm)
Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска.
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
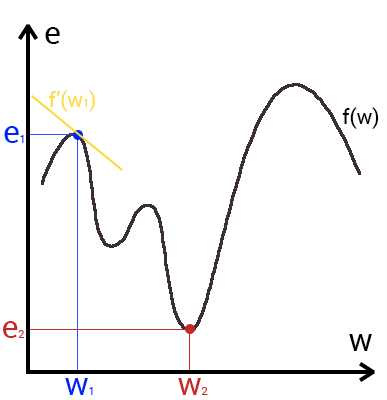
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
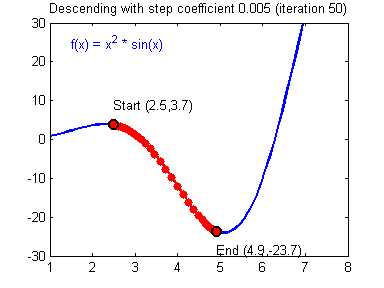
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
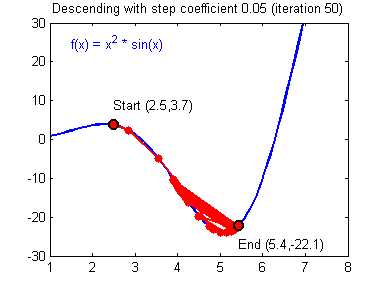
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке:
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
Данные задачи из предыдущей статьи
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
h2input = 1*0.45+0*-0.12=0.45
h2output = sigmoid(0.45)=0.61
h3input = 1*0.78+0*0.13=0.78
h3output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.
Так как у выходного нейрона нет исходящих синапсов, то мы будем пользоваться первой формулой (δ output), следственно для скрытых нейронов мы уже будем брать вторую формулу (δ hidden). Тут все достаточно просто: считаем разницу между желаемым и полученным результатом и умножаем на производную функции активации от входного значения данного нейрона. Прежде чем приступить к вычислениям я хочу обратить ваше внимание на производную. Во первых как это уже наверное стало понятно, с МОР нужно использовать только те функции активации, которые могут быть дифференцированы. Во вторых чтобы не делать лишних вычислений, формулу производной можно заменить на более дружелюбную и простую формула вида:
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.РешениеO1output = 0.33
O1ideal = 1
Error = 0.45
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для h2:Решениеh2output = 0.61
w5 = 1.5
δO1 = 0.148
δh2 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:Решениеh2output = 0.61
δO1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
РешениеE = 0.7Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0
Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для h3.Решениеh3output = 0.69
w6 = -2.3
δO1 = 0.148
E = 0.7
Α = 0.3
Δw6(i-1) = 0
δh3 = ( (1 — 0.69) * 0.69 ) * ( -2.3 * 0.148 ) = -0.07
GRADw6 = 0.69 * 0.148 = 0.1
Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
w6 = w6 + Δw6 = -2.2
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.Решениеw1 = 0.45, Δw1(i-1) = 0
w2 = 0.78, Δw2(i-1) = 0
w3 = -0.12, Δw3(i-1) = 0
w4 = 0.13, Δw4(i-1) = 0
δh2 = 0.053
δh3 = -0.07
E = 0.7
Α = 0.3
GRADw1 = 1 * 0.053 = 0.053
GRADw2 = 1 * -0.07 = -0.07
GRADw3 = 0 * 0.053 = 0
GRADw4 = 0 * -0.07 = 0
Δw1 = 0.7 * 0.053 + 0 * 0.3 = 0.04
Δw2 = 0.7 * -0.07 + 0 * 0.3 = -0.05
Δw3 = 0.7 * 0 + 0 * 0.3 = 0
Δw4 = 0.7 * 0 + 0 * 0.3 = 0
w1 = w1 + Δw1 = 0.5
w2 = w2 + Δw2 = 0.73
w3 = w3 + Δw3 = -0.12
w4 = w4 + Δw4 = 0.13
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.РешениеI1 = 1
I2 = 0
w1 = 0.5
w2 = 0.73
w3 = -0.12
w4 = 0.13
w5 = 1.563
w6 = -2.2
h2input = 1 * 0.5 + 0 * -0.12 = 0.5
h2output = sigmoid(0.5) = 0.62
h3input = 1 * 0.73 + 0 * 0.124 = 0.73
h3output = sigmoid(0.73) = 0.675
O1input = 0.62* 1.563 + 0.675 * -2.2 = -0.51
O1output = sigmoid(-0.51) = 0.37
O1ideal = 1 (0xor1=1)
Error = ((1-0.37)^2)/1=0.39
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
- Момент и скорость обучения
- Количество скрытых слоев
- Количество нейронов в каждом слое
- Наличие или отсутствие нейронов смещения
В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети.

Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
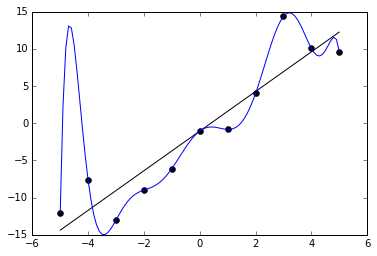
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.
Надеюсь эта статья смогла прояснить ключевые моменты такого нелегко предмета, как Нейронные сети. Однако я считаю, что сколько бы ты статей не прочел, без практики такую сложную тему освоить невозможно. Поэтому, если вы только в начале пути и хотите изучить эту перспективную и развивающуюся отрасль, то советую начать практиковаться с написания своей НС, а уже после прибегать к помощи различных фреймворков и библиотек. Также, если вам интересен мой метод изложения информации и вы хотите, чтобы я написал статьи на другие темы связанные с Машинным обучением, то проголосуйте в опросе ниже за ту тему которую вам интересна. До встречи в будущих статьях 🙂
habr.com
Пощупать нейросети или конструктор нейронных сетей / Habr
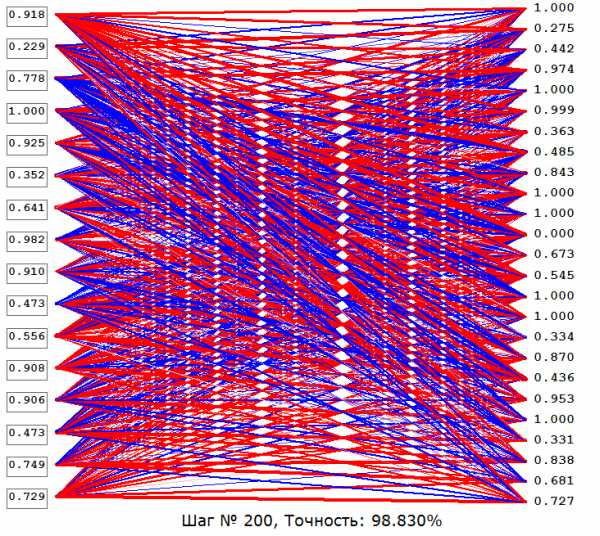
Я давно интересовался нейросетями, но только с позиции зрителя – следил за новыми возможностями, которые они дают по сравнению с обычным программированием. Но никогда не лез ни в теорию, ни в практику. И вдруг (после сенсационной новости о AlphaZero) мне захотелось сделать свою нейросеть. Посмотрев несколько уроков по этой теме на YouTube, я немного врубился в теорию и перешёл к практике. В итоге я сделал даже лучше, чем свою нейросеть. Получился конструктор нейросетей и наглядное пособие по ним (то есть можно смотреть, что творится внутри нейросети). Вот как это выглядит:
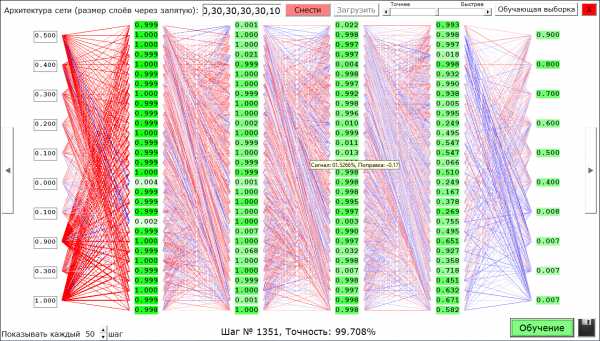
А теперь немного подробнее. С помощью этого конструктора можно создавать сети прямого распространения (Feedforward neural network) до 8 скрытых слоёв (плюс слой входов и слой выходов, итого 10 слоёв (обычно 4-х слоёв более чем достаточно)) в каждом слое до 30 нейронов (ограничение связано с тем, что всё это одновременно отображается на экране, если будут просьбы в комментариях выпущу версию без ограничений и визуализации). Функция активации всех нейронов – сигмоид на основе логистической функции. Также можно обучать получившиеся сети методом обратного распространения ошибки градиентным спуском по заданным примерам. И, самое главное, можно посмотреть на каждый нейрон в каждом отдельном случае (какое значение он передаёт дальше, его смещение (поправку, bias) – нейроны с отрицательным смещением белые, с положительным – ярко-зелёные), связи нейронов в зависимости от их веса помечены красным – положительные, синим – отрицательные, а также отличаются по толщине – чем больше модуль веса, тем толще. А если навести мышку на нейрон, то можно ещё посмотреть какой сигнал на него приходит, и какое конкретно у него смещение. Это полезно, чтобы понять, как работает конкретная сеть или показать студентам принцип работы сетей прямого распространения. Но самое главное – свою сеть можно сохранить в файл и поделиться с миром.
Далее будут инструкции по пользованию программой, встраиванию созданных сетей в свои проекты, а также разбор нескольких сетей, идущих в комплекте.
Как пользоваться конструктором
Для начала скачайте архив отсюда.
Распакуйте в корень диска D:\
Запустите NeuroNet.exe
Можете попробовать «Загрузить» какую-нибудь сеть, посмотреть на неё, нажать «Обучение», увидеть её точность, потыкать стрелки влево, вправо (по бокам), чтобы посмотреть различные варианты входных (левый столбец нейронов) и выходных (правый) данных, нажать «Стоп» и попробовать ввести свои входные данные (разрешены любые значения от 0 до 1, учитывайте это при создании своих сетей и нормализуйте входные и выходные данные).
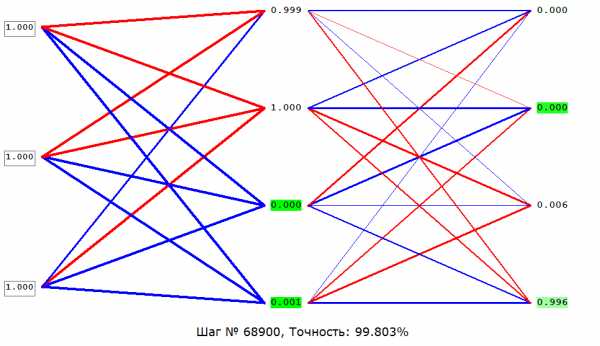
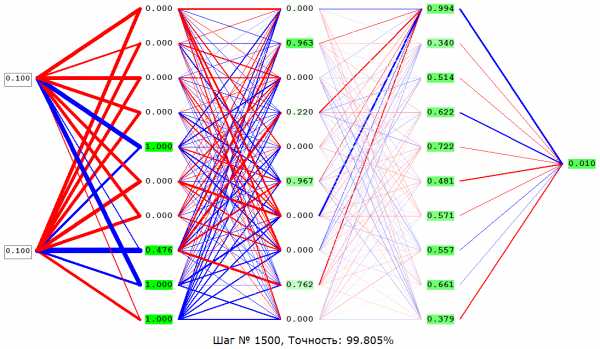
Теперь как строить свои сети. Первым делом необходимо задать архитектуру сети (количество нейронов в каждом слое через запятую), нажать «Построить» (или сначала «Снести», затем построить, если у Вас на экране уже отображается другая сеть), нажать «Обучающая выборка», «Удалить всё» и ввести свои обучающие примеры, согласно инструкции на экране. Также можно указать на вход и на выход маленькие квадратные картинки (максимум 5х5 пикселей), из которых будут определены нормализованные значения яркости пикселей (не учитывая их цвет), для чего нужно нажать на «in» и «out» соответственно. Нажать «Добавить пример», повторить процедуру нужное количество раз. Нажать «Готово», «Обучение» и как точность станет удовлетворительной (обычно 98%), нажать «Стоп», иконку в виде дискеты (сохранить), дать сети имя и радоваться, что Вы сами создали нейросеть. Дополнительно можете устанавливать скорость обучения ползунком «Точнее/Быстрее», а также визуализировать не каждый 50й шаг, а каждый 10й или 300й, как Вам угодно.
Интеграция созданных сетей в свои проекты
Чтобы использовать свои нейросети в собственных проектах, я создал отдельное приложение
doNet.exe, которое нужно запускать с параметрами: «D:\NeuroNet\doNet.exe <название сети> <входные данные через пробел>», дождаться завершения работы приложения, после чего считать выходные данные из D:\NeuroNet\temp.txtДля примера создано приложение 4-5.exe, использующее сеть «4-5» (об этой и других сетях ниже). В этом приложении подробно расписано как правильно запускать doNet.exe
Разбор сетей, идущих в комплекте
Начнём с классики – «XOR(Полусумматор)». Среди прочих, в частности, эту задачу – сложение по модулю 2 – в 1969 году приводили в качестве примера ограниченности нейросетей (а именно однослойных перцептронов). В общем, имеется два входа (со значениями либо 0, либо 1 у каждого), наша же задача — ответить 1, если значения входов разные, 0 – если одинаковые.
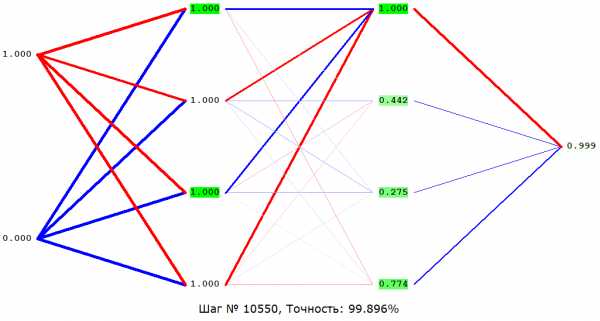
Далее «Количество-единиц». Три входа (0 либо 1 на каждом). Требуется посчитать, сколько было подано единиц. Реализовано как задача классификации – четыре выхода на каждый вариант ответа (0,1,2,3 единицы). На каком выходе максимальное значение, соответственно таков и ответ.
«Умножение» – Два входа (вещественные от 0 до 1), на выход их произведение.
«4-5» – На вход подаются нормализованные значения яркости пикселей картинки 4х4, на выходе имеем нормализованные значения яркости пикселей картинки 5х5.
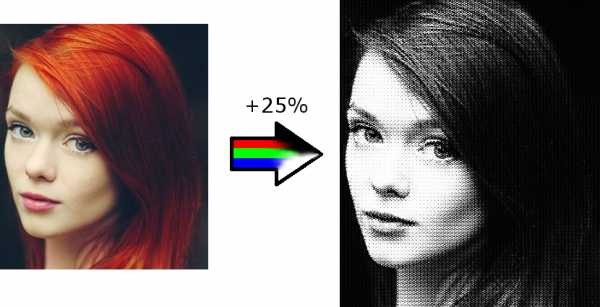
Сеть задумывалась, как увеличение качества большой картинки на 25%, вышел же интересный фильтр для фото:
UPD: В архив добавлено приложение NeuroNet2.exe (тот же конструктор, но без визуализации (благодаря чему работает в 2 раза быстрее) и ограничений на количество нейронов в слое (до 1024 вместо 30), также в обучающей выборке на вход и выход можно подавать квадратные картинки до 32х32). Также добавлен график обучения. Нейросетями теперь могут пользоваться (и встраивать в свои проекты (даже на сервере)) и те, кто не знает их теории! В полуавтоматическом режиме (после обучения вручную подавать на вход значения и получать результат на экране) их можно использовать даже без знания программирования!
Вот собственно и всё, жду комментариев.
P.S. Если вылезает ошибка, попробуйте зарегистрировать от администратора с помощью regsvr32 файлы comdlg32, которые также есть в архиве.
habr.com
пятиминутный гид для новичков / Neurodata Lab corporate blog / Habr
С момента описания первого искусственного нейрона Уорреном Мак-Каллоком и Уолтером Питтсом прошло более пятидесяти лет. С тех пор многое изменилось, и сегодня нейросетевые алгоритмы применяются повсеместно. И хотя нейронные сети способны на многое, исследователи при работе с ними сталкиваются с рядом трудностей: от переобучения до проблемы «черного ящика».Если термины «катастрофическая забывчивость» и «регуляризация весов» вам пока ни о чем не говорят, читайте дальше: попробуем разобраться во всем по порядку.
 / Фотография Jun / CC-SA
/ Фотография Jun / CC-SA
За что мы любим нейросети
Основное преимущество нейронных сетей перед другими методами машинного обучения состоит в том, что они могут распознавать более глубокие, иногда неожиданные закономерности в данных. В процессе обучения нейроны способны реагировать на полученную информацию в соответствии с принципами генерализации, тем самым решая поставленную перед ними задачу.
К областям, где сети находят практическое применение уже сейчас, можно отнести медицину (например, очистка показаний приборов от шумов, анализ эффективности проведённого лечения), интернет (ассоциативный поиск информации), экономику (прогнозирование курсов валют, автоматический трейдинг), игры (например, го) и другие. Нейросети могут использоваться практически для чего угодно в силу своей универсальности. Однако волшебной таблеткой они не являются, и чтобы они начали функционировать должным образом, требуется проделать много предварительной работы.
Обучение нейросетей 101
Одним из ключевых элементов нейронной сети является способность обучаться. Нейронная сеть — это адаптивная система, умеющая изменять свою внутреннюю структуру на базе поступающей информации. Обычно такой эффект достигается с помощью корректировки значений весов.
Связи между нейронами на соседних слоях нейросети — это числа, описывающие значимость сигнала между двумя нейронами. Если обученная нейронная сеть верно реагирует на входную информацию, то настраивать веса нет необходимости, а в противном случае с помощью какого-либо алгоритма обучения нужно изменить веса, улучшив результат.
Как правило, это делают с помощью метода обратного распространения ошибки: для каждого из обучающих примеров веса корректируются так, чтобы уменьшить ошибку. Считается, что при правильно подобранной архитектуре и достаточном наборе обучающих данных сеть рано или поздно обучится.
Существует несколько принципиально отличающихся подходов к обучению, в привязке к поставленной задаче. Первый — обучение с учителем. В этом случае входные данные представляют собой пары: объект и его характеристику. Такой подход применяется, например, в распознавании изображений: обучение проводится по размеченной базе из картинок и расставленных вручную меток того, что на них нарисовано.
Самой известной из таких баз является ImageNet. При такой постановке задачи обучение мало чем отличается от, например, распознавания эмоций, которым занимается Neurodata Lab. Сети демонстрируются примеры, она делает предположение, и, в зависимости от его правильности, корректируются веса. Процесс повторяется до тех пор, пока точность не увеличивается до искомых величин.
Второй вариант — обучение без учителя. Типичными задачами для него считаются кластеризация и некоторые постановки задачи поиска аномалий. При таком раскладе истинные метки обучающих данных нам недоступны, но есть необходимость в поиске закономерностей. Иногда схожий подход применяют для предобучения сети в задаче обучения с учителем. Идея состоит в том, чтобы начальным приближением для весов было не случайное решение, а уже умеющее находить закономерности в данных.
Ну и третий вариант — обучение с подкреплением — стратегия, построенная на наблюдениях. Представьте себе мышь, бегущую по лабиринту. Если она повернет налево, то получит кусочек сыра, а если направо — удар током. Со временем мышь учится поворачивать только налево. Нейронная сеть действует точно так же, подстраивая веса, если итоговый результат — «болезненный». Обучение с подкреплением активно применяется в робототехнике: «ударился ли робот в стену или остался невредим?». Все задачи, имеющие отношение к играм, в том числе самая известная из них — AlphaGo, основаны именно на обучении с подкреплением.
Переобучение: в чем проблема и как ее решить
Главная проблема нейросетей — переобучение. Оно заключается в том, что сеть «запоминает» ответы вместо того, чтобы улавливать закономерности в данных. Наука поспособствовала появлению на свет нескольких методов борьбы с переобучением: сюда относятся, например, регуляризация, нормализация батчей, наращивание данных и другие. Иногда переобученная модель характеризуется большими абсолютными значениями весов.
Механизм этого явления примерно такой: исходные данные нередко сильно многомерны (одна точка из обучающей выборки изображается большим набором чисел), и вероятность того, что наугад взятая точка окажется неотличимой от выброса, будет тем больше, чем больше размерность. Вместо того, чтобы «вписывать» новую точку в имеющуюся модель, корректируя веса, нейросеть как будто придумывает сама себе исключение: эту точку мы классифицируем по одним правилам, а другие — по другим. И таких точек обычно много.
Очевидный способ борьбы с такого рода переобучением – регуляризация весов. Она состоит либо в искусственном ограничении на значения весов, либо в добавлении штрафа в меру ошибки на этапе обучения. Такой подход не решает проблему полностью, но чаще всего улучшает результат.
Второй способ основан на ограничении выходного сигнала, а не значений весов, — речь о нормализации батчей. На этапе обучения данные подаются нейросети пачками — батчами. Выходные значения для них могут быть какими угодно, и тем их абсолютные значения больше, чем выше значения весов. Если из каждого из них мы вычтем какое-то одно значение и поделим результат на другое, одинаково для всего батча, то мы сохраним качественные соотношения (максимальное, например, все равно останется максимальным), но выход будет более удобным для обработки его следующим слоем.
Третий подход работает не всегда. Как уже говорилось, переобученная нейросеть воспринимает многие точки как аномальные, которые хочется обрабатывать отдельно. Идея состоит в наращивании обучающей выборки, чтобы точки были как будто той же природы, что и исходная выборка, но сгенерированы искусственно. Однако тут сразу рождается большое число сопутствующих проблем: подбор параметров для наращивания выборки, критическое увеличение времени обучения и прочие.
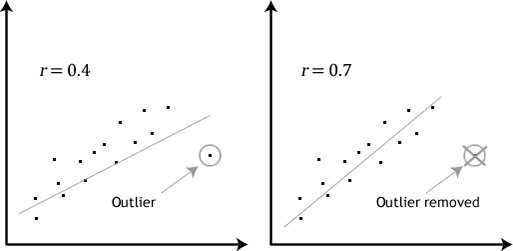
Эффект от удаления аномального значения из тренировочного свода данных (источник)
В обособленную проблему выделяется поиск настоящих аномалий в обучающей выборке. Иногда это даже рассматривают как отдельную задачу. Изображение выше демонстрирует эффект исключения аномального значения из набора. В случае нейронных сетей ситуация будет аналогичной. Правда, поиск и исключение таких значений — нетривиальная задача. Для этого применяются специальные техники — подробнее о них вы можете прочитать по ссылкам (здесь и здесь).
Одна сеть – одна задача или «проблема катастрофической забывчивости»
Работа в динамически изменяющихся средах (например, в финансовых) сложна для нейронных сетей. Даже если вам удалось успешно натренировать сеть, нет гарантий, что она не перестанет работать в будущем. Финансовые рынки постоянно трансформируются, поэтому то, что работало вчера, может с тем же успехом «сломаться» сегодня.
Здесь исследователям или приходится тестировать разнообразные архитектуры сетей и выбирать из них лучшую, или использовать динамические нейронные сети. Последние «следят» за изменениями среды и подстраивают свою архитектуру в соответствии с ними. Одним из используемых в этом случае алгоритмов является метод MSO (multi-swarm optimization).
Более того, нейросети обладают определенной особенностью, которую называют катастрофической забывчивостью (catastrophic forgetting). Она сводится к тому, что нейросеть нельзя последовательно обучить нескольким задачам — на каждой новой обучающей выборке все веса нейронов будут переписаны, и прошлый опыт будет «забыт».
Безусловно, ученые трудятся над решением и этой проблемы. Разработчики из DeepMind недавно предложили способ борьбы с катастрофической забывчивостью, который заключается в том, что наиболее важные веса в нейронной сети при выполнении некой задачи А искусственно делаются более устойчивыми к изменению в процессе обучения на задаче Б.
Новый подход получил название Elastic Weight Consolidation (упругое закрепление весов) из-за аналогии с упругой пружинкой. Технически он реализуется следующим образом: каждому весу в нейронной сети присваивается параметр F, который определяет его значимость только в рамках определенной задачи. Чем больше F для конкретного нейрона, тем сложнее будет изменить его вес при обучении новой задаче. Это позволяет сети «запоминать» ключевые навыки. Технология уступила «узкоспециализированным» сетям в отдельных задачах, но показала себя с лучшей стороны по сумме всех этапов.
Армированный черный ящик
Еще одна сложность работы с нейронными сетями состоит в том, что ИНС фактически являются черными ящиками. Строго говоря, кроме результата, из нейросети не вытащишь ничего, даже статистические данные. При этом сложно понять, как сеть принимает решения. Единственный пример, где это не так — сверточные нейронные сети в задачах распознавания. В этом случае некоторые промежуточные слои имеют смысл карт признаков (одна связь показывает то, встретился ли какой-то простой шаблон в исходной картинке), поэтому возбуждение различных нейронов можно отследить.
Разумеется, указанный нюанс делает достаточно сложным использование нейронных сетей в приложениях, когда ошибки критичны. Например, менеджеры фондов не могут понять, как нейронная сеть принимает решения. Это приводит к тому, что невозможно корректно оценить риски торговых стратегий. Аналогично банки, прибегающие к нейронным сетям для моделирования кредитных рисков, не смогут сказать, почему этот самый клиент имеет сейчас именно такой кредитный рейтинг.
Поэтому разработчики нейросетей ищут способы обойти это ограничение. Например, работа ведется над так называемыми алгоритмами изъятия правил (rule-extraction algorithms), чтобы повысить прозрачность архитектур. Эти алгоритмы извлекают информацию из нейросетей либо в виде математических выражений и символьной логики, либо в виде деревьев решений.
Нейронные сети — это лишь инструмент
Само собой, искусственные нейронные сети активно помогают осваивать новые технологии и развивать существующие. Сегодня на пике популярности находится программирование беспилотных автомобилей, в которых нейросети в режиме реального времени анализируют окружающую обстановку. IBM Watson из года в год открывает для себя всё новые прикладные области, включая медицину. В Google существует целое подразделение, которое занимается непосредственно искусственным интеллектом.
Вместе с тем порой нейронная есть — не лучший способ решить задачу. Например, сети «отстают» по таким направлениям, как создание изображений высокого разрешения, генерация человеческой речи и глубокий анализ видеопотоков. Работа с символами и рекурсивными структурами также даётся нейросистемам нелегко. Верно это и для вопросно-ответных систем.
Изначально идея нейронных сетей заключалась в копировании и даже воссоздании механизмов функционирования мозга. Однако человечеству по-прежнему нужно разрешить проблему скорости работы нейронных сетей, разработать новые алгоритмы логического вывода. Существующие алгоритмы по меньшей мере в 10 раз уступают возможностям мозга, что неудовлетворительно во многих ситуациях.
При этом ученые до сих пор не до конца определились, в каком направлении следует развивать нейросети. Индустрия старается как максимально приблизить нейросети к модели человеческого мозга, так и генерировать технологии и концептуальные схемы, абстрагируясь ото всех «аспектов человеческой природы». На сегодняшний день — это что-то вроде «открытого произведения» (если воспользоваться термином Умберто Эко), где практически любые опыты допустимы, а фантазии – приемлемы.
Деятельность ученых и разработчиков, занимающихся нейросетями, требует глубокой подготовки, обширных знаний, использования нестандартных методик, поскольку нейросеть сама по себе — это не «серебряная пуля», способная решить любые проблемы и задачи без участия человека. Это комплексный инструмент, который в умелых руках может делать удивительные вещи. И у него еще всё впереди.
habr.com
Введение в архитектуры нейронных сетей
Григорий Сапунов (Intento)
Меня зовут Григорий Сапунов, я СТО компании Intento. Занимаюсь я нейросетями довольно давно и machine learning’ом, в частности, занимался построением нейросетевых распознавателей дорожных знаков и номеров. Участвую в проекте по нейросетевой стилизации изображений, помогаю многим компаниям.
Давайте перейдем сразу к делу. Моя цель — дать вам базовую терминологию и понимание, что к чему в этой области, из каких кирпичиков собираются нейросети, и как это использовать.
План доклада такой. Сначала небольшое введение про то, что такое нейрон, нейросеть, глубокая нейросеть, чтобы мы с вами общались на одном языке.
Дальше я расскажу про важные тренды, что происходит в этой области. Затем мы углубимся в архитектуру нейросетей, рассмотрим 3 основных их класса. Это будет самая содержательная часть.
После этого рассмотрим 2 сравнительно продвинутых темы и закончим небольшим обзором фреймворков и библиотек для работы с нейросетями.
На конференции Наталья Ефремова из компании NTechLab рассказывала о практических кейсах. Я же расскажу, как нейросети устроены внутри, из каких кирпичиков они внутри состоят.
Краткое содержание

Recap: нейрон, нейросеть, глубокая нейросеть
Краткое напоминание
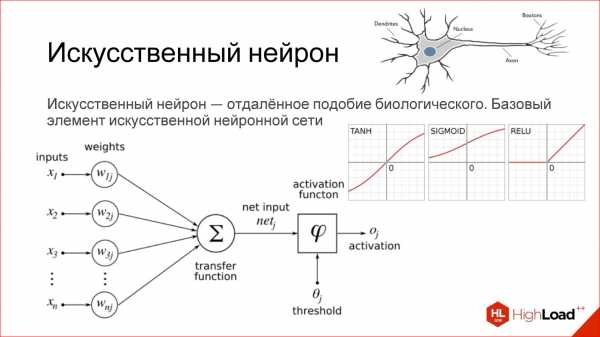
Искусственный нейрон — это очень отдаленное подобие биологического нейрона.
Что такое искусственный нейрон? Это простая функция на самом деле. У нее есть входы. Каждый вход умножается на некие веса, дальше все суммируется, прогоняется через какую-то нелинейную функцию, результат выдается на выход — все, это один нейрон.
Если вы знакомы с логистической регрессией, под которой понимаем нелинейную функцию SIGMOID, то один нейрон — это полный аналог логистической регрессии, простого линейного классификатора.
На самом деле существует много разных функций активации, в том числе приведенные на рисунке гиперболический тангенс (TANH), SIGMOID, RELU.
В реальности все сильно сложнее. Этой темы касаться не будем.
Я привел совсем базовое представление искусственного нейрона, как некое подобие биологического нейрона.
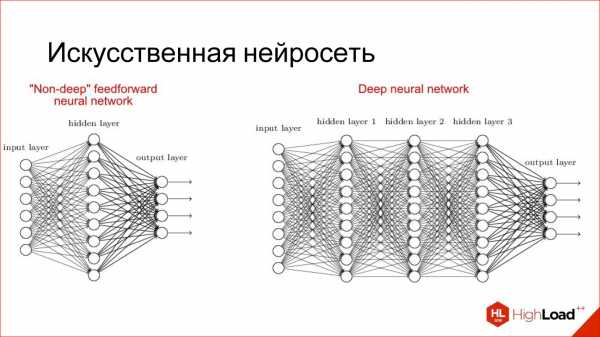
Искусственная нейросеть — это способ собрать нейроны в сеть, чтобы она решала определенную задачу, например, задачу классификации. Нейроны собираются по слоям. Есть входной слой, куда подается входной сигнал, есть выходной слой, откуда снимается результат работы нейросети, и между ними есть скрытые слои. Их может быть 1, 2, 3, много. Если скрытых слоев больше, чем 1, нейросеть считается глубокой, если 1, то неглубокой.

Существует огромное разнообразие различных архитектур, основные из которых мы рассмотрим. Но имейте в виду, что их очень много. Если интересно, перейдите потом по ссылке – посмотрите, почитайте.
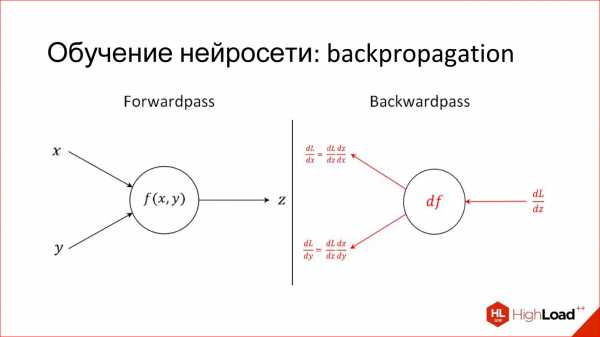
Еще одна полезная вещь, которую нужно знать для обсуждения нейросетей. Я уже рассказал, как работает один нейрон: как каждый вход умножает на веса, на коэффициенты, суммирует, умножает на нелинейность. Это, скажем так, продакшн-режим работы нейрона, то есть inference, как он работает в уже обученном виде.
Есть совсем другая задача — обучить нейрон. Обучение заключается в том, чтобы найти эти правильные веса. Обучение построено на простой идее, что если мы на выходе нейрона знаем, какой должен быть ответ, и знаем, какой он получился, нам становится известна эта разница, ошибка. Эту ошибку можно отправить обратно ко всем входам нейрона и понять, какой вход насколько сильно повлиял на эту ошибку, и соответственно, подкорректировать вес на этом входе так, чтобы ошибку уменьшить.
Это основная идея Backpropagation, алгоритма обратного распространения ошибки. Этот процесс можно прогнать по всей сети и для каждого нейрона найти, как его веса можно модифицировать. Для этого нужно взять производные, но в принципе в последнее время это не требуется. Все пакеты для работы с нейросетями автоматически дифференцируют. Если еще 2 года назад надо было вручную писать сложные производные для хитрых слоев, то сейчас пакеты делают это сами.
Recap: важные тренды
Что сейчас происходит с качеством и сложностью моделей
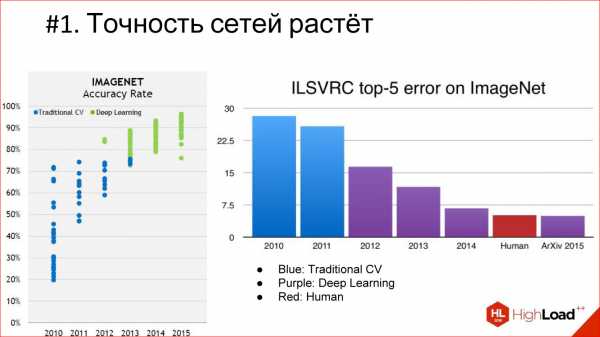
Во-первых, точность нейросетей растет, и очень сильно растет. Уже есть несколько примеров, когда нейросети приходят в какую-то область и вытесняют целиком классический алгоритм. Так уже было в обработке изображений и в распознавании речи, так произойдет еще в разных областях. То есть появляются нейросети, которые очень сильно уменьшают ошибку.
На диаграмме фиолетовым цветом выделен Deep Learning, голубым – классический алгоритм компьютерного зрения. Видно, что появился Deep Learning, ошибка уменьшилась и продолжает уменьшаться дальше. Именно поэтому Deep Learning целиком вытесняет все, условно, классические алгоритмы.
Другая важная веха — то, что мы начинаем обгонять по качеству человека. На соревновании ImageNet это впервые произошло в 2015 году. Но на самом деле нейросетевые системы, которые по качеству превосходят человека, появились раньше. Первый задокументированный внятный случай — это 2011 год, когда была построена система, которая распознавала немецкие дорожные знаки и делала это в 2 раза лучше человека.
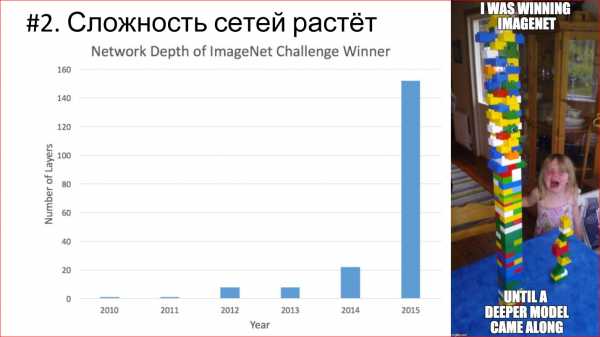
Второй важный тренд — сложность нейросетей растет. В терминах глубины растет глубина. Если победитель 2012 года на ImageNet — сеть AlexNet — там было меньше 10 слоев, то в 2014 году их было уже больше 20, в 2015 — под 150. В этом году, кажется, уже за 200. Что будет дальше — непонятно, возможно, будет еще больше.
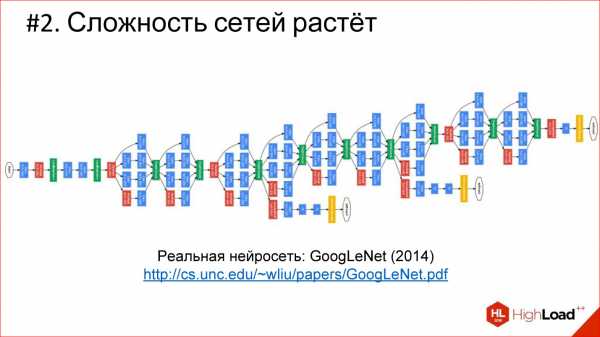
http://cs.unc.edu/~wliu/papers/GoogLeNet.pdf
Кроме того, что растет глубина, растет и сама архитектурная сложность. Вместо того, чтобы слои просто стыковать один за другим, они начинают ветвиться, появляются блоки, структура. В общем, архитектурная сложность тоже растет.
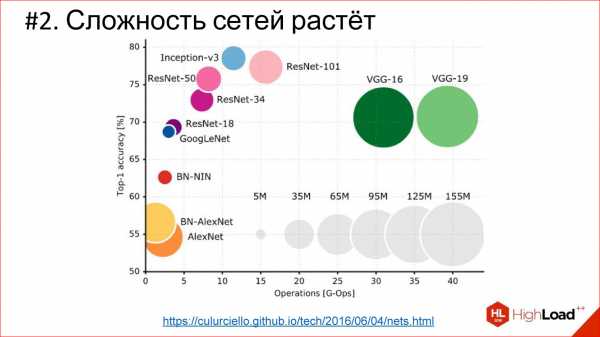
https://culurciello.github.io/tech/2016/06/04/nets.html
Это график точности различных нейросетей. Здесь указано время, которое требуется на выполнение, на просчет этой сети, то есть некая вычислительная нагрузка. Размер кружка — это количество параметров, которые описываются нейросетью. Интересно сравнить классическую сеть AlexNet — победителя 2012 года и более поздние сети. Они лучше по точности, но, как правило, содержат меньше параметров. Это тоже важный тренд, что нейросети усложняются очень умно. То есть архитектура изменяется так, что даже несмотря на то, что число слоев 150, общее количество параметров оказывается меньше, чем в 6-7-слойной сети, которая в 2012 году была. Архитектура как-то усложняется очень интересным способом.
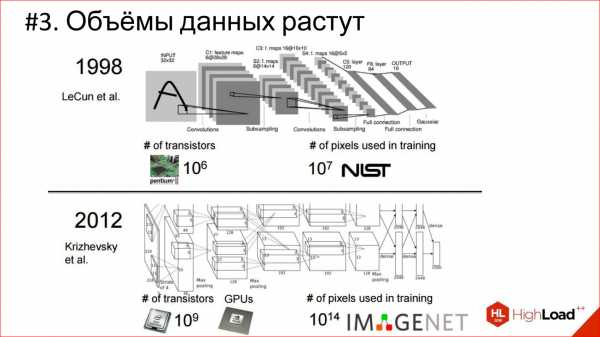
Еще один тренд — рост объемов данных. В 1998 году для обучения сверточной
нейросети, которая распознавала рукописные чеки, было использовано 10 7 пикселей, в 2012 году (IMAGENET) — 10 14.
7 порядков за 14 лет — это безумная разница и огромный сдвиг!
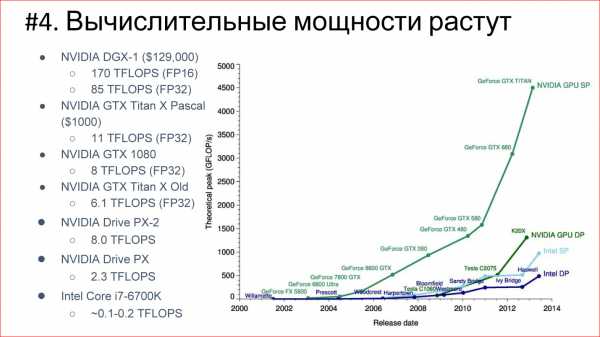
При этом количество транзитов на процессоре тоже растет, растут вычислительные мощности — закон Мура действует. За эти 14 лет процессоры стали условно в 1000 раз быстрее. Это видно на примере GPUs, которые сейчас доминируют в области Deep Learning. Практически все считается на графических ускорителях.
Компания NVIDIA перепрофилировалась из игровой фактически в компанию для искусственного интеллекта. Ее экспоненты оставили далеко позади экспоненты Intel, которые на этом фоне вообще не смотрятся.
Это картинка 2013 года, когда топовая видеокарта была 4,5 TFLOPS. Сейчас новый TITAN X — это уже 11 TFLOPS. В общем, экспонента продолжается!
На самом деле можно ожидать, что в ближайшее время появится FPGA’сики, которые частично потеснят GPU, и, может быть, со временем появятся даже нейроморфные процессоры. Следите за этим — там тоже много интересного происходит.
Архитектуры нейросетей. Нейросети прямого распространения
Fully Connected Feed-Forward Neural Networks, FNN
Первая классическая архитектура — полносвязные нейросети прямого распространения, или Fully Connected Feed-Forward Neural Network, FNN.

Многослойный Perceptron — это вообще классика нейросетей. Та картинка нейросетей, которую вы видели, это он и есть — многослойная полносвязная сеть. Полносвязная — это значит, что каждый нейрон связан со всеми нейронами предыдущего слоя. Хорошая сеть, работает, для классификации годится, многие задачи классификации успешно решаются.
Однако у нее есть 2 проблемы:
- Много параметров
Например, если взять нейросеть из 3 скрытых слоев, которой нужно обрабатывать картинки 100*100 ps, это значит, что на входе будет 10 000 ps, и они заводятся на 3 слоя. В общем, если честно посчитать все параметры, у такой сети их будет порядка миллиона. Это на самом деле много. Чтобы обучить нейросеть с миллионом параметров, нужно очень много обучающих примеров, которые не всегда есть. На самом деле сейчас примеры есть, а раньше их не было — поэтому, в частности, сети не могли обучать, как следует.
Кроме того, сеть, у которой много параметров, имеет дополнительную склонность переобучаться. Она может заточиться на то, чего в реальности не существует: какой-то шум Data Set. Даже если, в конце концов, сеть запомнит примеры, но на тех, которых она не видела, потом не сможет нормально использоваться.
Плюс есть другая проблема под названием:
- Затухающие градиенты
Помните ту историю про Backpropagation, когда ошибка с выходов отправляется на вход, распределяется по всем весам и отправляется дальше по сети? Далее эти производные — то есть градиент (производная ошибки) — прогоняются через нейросеть обратно. Когда в нейросети много слоев, от этого градиента в самом конце может остаться очень-очень маленькая часть. В этом случае веса на входе будет практически невозможно изменить потому, что этот градиент практически «сдох», его там нет.
Это тоже проблема, из-за которой глубокие нейросети тоже сложно обучать. К этой теме мы еще вернемся дальше, особенно на рекуррентных сетях.

Есть различные вариации FNN-сетей. Например, очень интересная вариация Автоэнкодер. Это сеть прямого распространения с так называемым бутылочным горлышком в середине. Это очень маленький слой, допустим, всего на 10 нейронов.
В чем преимущества такой нейросети?
Цель этой нейросети взять какой-то вход, прогнать через себя и на выходе сгенерировать тот же самый вход, то есть чтобы они совпадали. В чем смысл? Если мы сможем обучить такую сеть, которая берет вход, прогоняет через себя и генерирует точно такой же выход, это значит, что этих 10 нейронов в середине достаточно для описания этого входа. То есть можно очень сильно уменьшить пространство, сократить объём данных, экономно закодировать любые входные данные в новых терминах 10 векторов.
Это удобно, и это работает. Такие сети могут помочь вам, например, уменьшить размерность вашей задачи или найти какие-то интересные фичи, которые можно использовать.

Есть еще интересная модель RBM. Я ее написал в вариации FNN, но на самом деле это не правда. Во-первых, она не глубокая, во-вторых, она не Feed-Forward. Но она часто связана с FNN-сетями.
Что это такое?
Это неглубокая модель (на слайде она в уголке нарисована), у которой есть вход и есть какой-то скрытый слой. Вы подаете сигнал на вход и пытаетесь обучить скрытый слой так, чтобы он генерил этот вход.
Это генеративная модель. Если вы ее обучили, то потом можете генерить аналоги ваших входных сигналов, но чуть-чуть другие. Она стохастическая, то есть каждый раз она будет генерить что-то чуть другое. Если вы, например, обучили такую модель на генерацию рукописных единичек, она потом их нагенерит какое-то количество немножко разных.
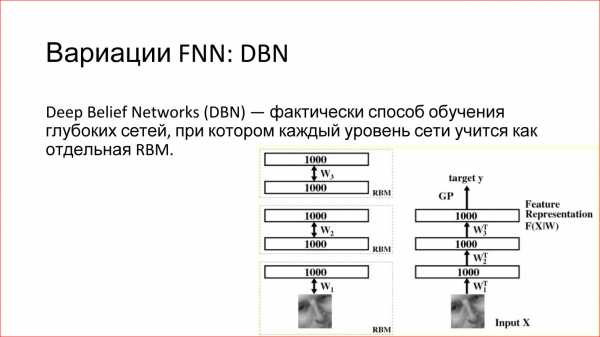
Чем хороши RBM — тем, что их можно использовать для обучения глубоких сетей. Есть такой термин — Deep Belief Networks (DBN) — фактически это способ обучения глубоких сетей, когда берутся отдельно 2 нижних слоя глубокой сети, подается вход и RBM обучается на этих первых двух слоях. После этого фиксируются эти веса. Далее берется второй слой, рассматривается как отдельная RBM и точно также обучается. И так по всей сети. Потом эти RBM стыкуются, объединяются в одну нейросеть. Получается глубокая нейросеть, какая и должна была бы быть.
Но теперь есть огромное преимущество — если бы раньше вы ее обучали просто с какого-то рандомного (случайного) состояния, то теперь оно не рандомное – сеть обучена восстанавливать или генерить данные предыдущего слоя. То есть у нее веса разумные, и на практике это приводит к тому, что такие нейросети действительно уже довольно неплохо обучены. Их потом можно слегка дообучить какими-то примерами, и качество такой сети будет хорошим.
Плюс есть дополнительное преимущество. Когда вы используете RBM, вы, по сути, работаете на неразмеченных данных, что называется Un supervised learning. У вас есть просто картинки, вы не знаете их классов. Вы прогнали миллионы, миллиарды картинок, которые вы скачали с Flickr’а или еще откуда-то, и у вас есть какая-то структура в самой сети, которая описывает эти картинки.
Вы не знаете, что это такое еще, но это разумные веса, которые можно потом взять и дообучить небольшим количеством различных картинок, и уже будет хорошо. Это классный вариант использования комбинации 2 нейросетей.
Дальше вы увидите, что вся эта история на самом деле — про Lego. То есть у вас есть отдельные сети — рекуррентные нейросети, еще какие-то сети — это все блоки, которые можно совмещать. Они хорошо совмещаются на разных задачах.
Это были классические нейросети прямого распространения. Далее перейдем к сверточным нейросетям.
Архитектуры нейросетей: Сверточные нейросети
Convolutional Neural Networks, CNN
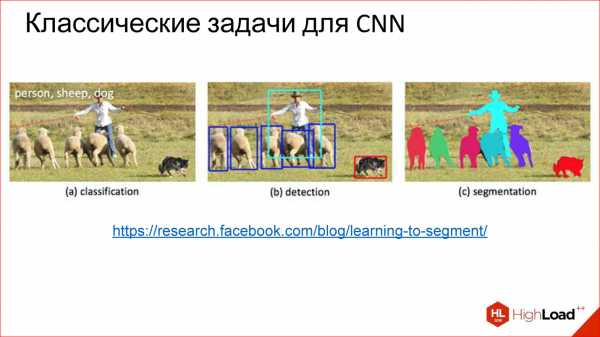
https://research.facebook.com/blog/learning-to-segment/
Сверточные нейросети решают 3 основные задачи:
- Классификация. Вы подаете картинку, и нейросеть просто говорит — у вас картинка про собаку, про лошадь, еще про что-то, и выдает класс.
- Детекция – это более продвинутая задачка, когда нейросеть не просто говорит, что на картинке есть собака или лошадь, но находит еще Bounding box — где это находится на картинке.
- Сегментация. На мой взгляд, это самая крутая задача. По сути, это попиксельная классификация. Здесь мы говорим про каждый пиксель изображения: этот пиксель относится к собаке, этот — к лошади, а этот еще к чему-то. На самом деле, если вы умеете решать задачу сегментации, то остальные 2 задачи уже автоматически даны.
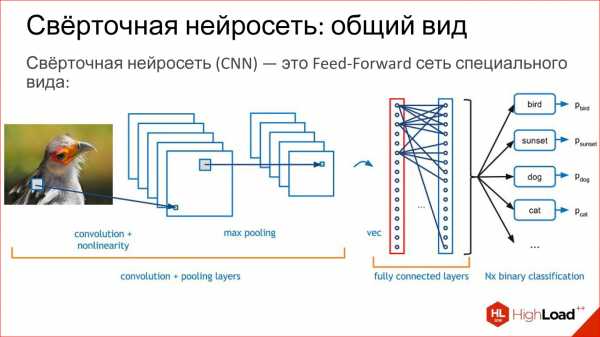
Что такое сверточная нейросеть? На самом деле сверточная нейросеть — это обычная Feed-Forward сеть, просто она немножко специального вида. Вот уже начинается Lego.
Что есть в сверточной сети? У нее есть:
- Сверточные слои — я дальше расскажу, что это такое;
- Subsampling, или Pooling-слои, которые уменьшают размер изображения;
- Обычные полносвязные слои, тот самый многослойный персептрон, который просто сверху навешен на эти первые 2 хитрых слоя.
Немного более подробно про все эти слои.

- Сверточные слои обычно рисуются в виде набора плоскостей или объемов. Каждая плоскость на таком рисунке или каждый срез в этом объеме — это, по сути, один нейрон, который реализует операцию свертки. Опять же, дальше я расскажу, что это такое. По сути, это матричный фильтр, который трансформирует исходное изображение в какое-то другое, и это можно делать много раз.
- Слои субдискретизации (буду называть Subsampling, так проще) просто уменьшают размер изображения: было 200*200 ps, после Subsampling стало 100*100 ps. По сути, усреднение, чуть более хитрое.
- Полносвязные слои обычно персептрон использует для классификации. Ничего специального в них нет.
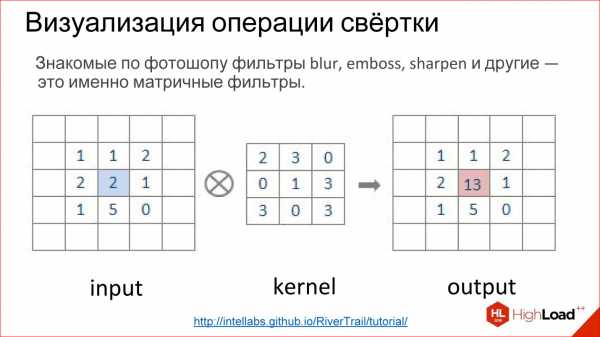
http://intellabs.github.io/RiverTrail/tutorial/
Что такое операция свертки? Это всех пугает, но на самом деле это очень простая вещь. Если вы работали в Photoshop и делали Gaussian Blur, Emboss, Sharpen и кучу других фильтров, это все матричные фильтры. Матричные фильтры — это на самом деле и есть операция свертки.
Как она реализована? Есть матрица, которая называется ядром фильтра (на рисунке kernel). Для Blur это будут все единицы. Есть изображение. Эта матрица накладывается на кусочек изображения, соответствующие элементы просто перемножаются, результаты складываются и записываются в центральную точку.
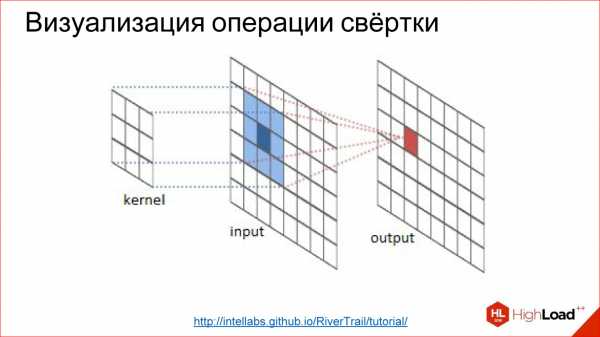
http://intellabs.github.io/RiverTrail/tutorial/
Так это выглядит более наглядно. Есть изображение Input, есть фильтр. Вы пробегаете фильтром по всему изображению, честно перемножаете соответствующие элементы, складываете, записываете в центр. Пробегаете, пробегаете — построили новое изображение. Все, это операция свертки.
То есть, по сути, свертка в сверточных нейросетях — это хитрый цифровой фильтр (Blur, Emboss, что угодно еще), который сам обучается.
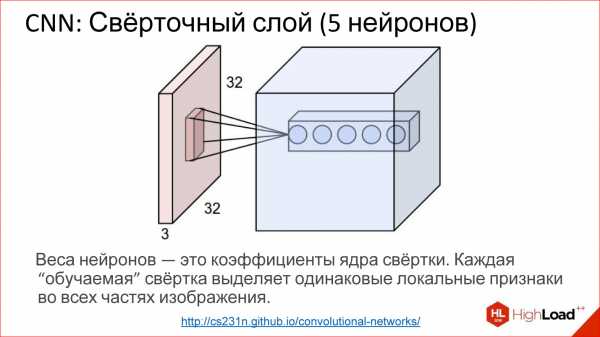
http://cs231n.github.io/convolutional-networks/
На самом деле сверточные слои все работают на объемах. То есть если даже взять обычное изображение RGB, там уже 3 канала — это, по сути, не плоскость, а объем из 3-х, условно, кубиков.
Свертка в этом случае уже представляется не матрицей, а тензором — кубиком на самом деле.
У вас есть фильтр, вы пробегаете по всему изображению, он сразу смотрит на все 3 цветовых слоя и генерит одну новую точку для одного этого объема. Пробегаете по всему изображению — построили один канал, одну плоскость нового изображения. Если у вас 5 нейронов — вы построили 5 плоскостей.
Так работает сверточный слой. Задача обучения сверточного слоя — это задача такая же, как в обычных нейросетях — найти веса, то есть фактически найти ту самую матрицу свертки, которая полностью эквивалентна весам в нейронах.
Что делают такие нейроны? Они фактически учатся искать какие-то фичи, какие-то локальные признаки в той небольшой части, которую они видят — и все. Прогон одного такого фильтра — это построение некой карты нахождения этих признаков в изображении.
Потом вы построили много таких плоскостей, дальше их используете как изображение, подавая на следующие входы.

Операция Pooling — еще более простая операция. Это просто усреднение либо взятие максимума. Она тоже работает на каких-то небольших квадратиках, например, 2*2. Вы накладываете на изображение и, например, выбираете максимальный элемент из этого квадратика 2*2, отправляете на выход.
Таким образом вы уменьшили изображение, но не хитрым Average, а чуть более продвинутой штукой — взяли максимум. Это дает небольшую инвариантность к смещениям. То есть вам не важно, какой-то признак нашелся в этой позиции или на 2 ps вправо. Эта штука позволяет нейросети быть чуть более устойчивой к сдвигам изображения.
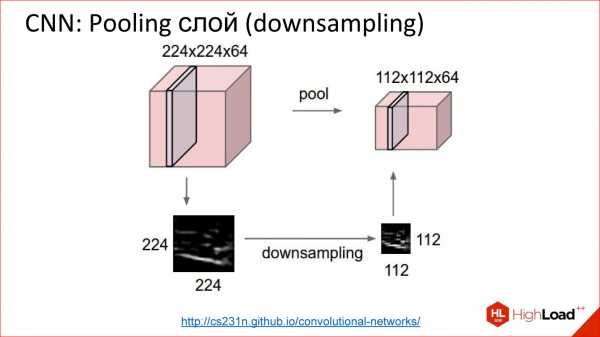
http://cs231n.github.io/convolutional-networks/
Так работает Pooling-слой. Есть кубик какого-то объема — 3 канала, 10, или 100 каналов, которые вы насчитали свертками. Он просто уменьшает его по ширине и по высоте, остальные размерности не трогает. Все — примитивная вещь.

Чем хороши сверточные сети?
Они хороши тем, что у них сильно меньше параметров, чем у обычной полносвязной сети. Вспомните пример с полносвязной сетью, который мы рассматривали, где получился миллион весов. Если взять аналогичную, точнее, похожую — аналогичной ее нельзя назвать, но близкую сверточную нейросеть, у которой будет такой же вход, такой же выход, тоже будет один полносвязный слой на выходе и еще 2 сверточных слоя, где тоже будет по 100 нейронов, как в базовой сети, то выяснится, что число параметров в такой нейросети уменьшилось больше, чем на порядок.
Это здорово, если параметров настолько меньше — сеть проще обучать. Мы это видим, ее действительно проще обучать.
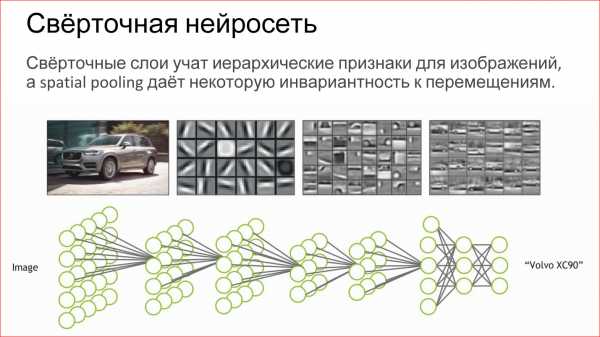
Что делает сверточная нейросеть?
По сути, она автоматически учит какие-то иерархические признаки для изображений: сначала базовые детекторы, линии разного наклона, градиенты и т.д. Из них она собирает какие-то более сложные объекты, потом еще более сложные.
Если вы воспринимаете нейрон как простую логистическую регрессию, простой классификатор, то нейросеть — это просто иерархический классификатор. Сначала вы выделяете простые признаки, из них комбинируете сложные признаки, из них еще более сложные, еще более сложные и в конце концов вы можете скомбинировать какой-то очень сложный признак — конкретный человек, конкретная машина, слон, что угодно еще.
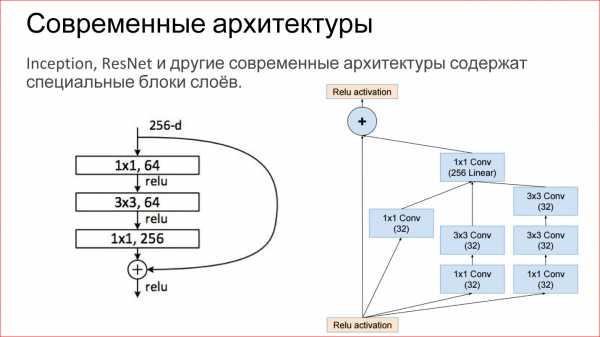
Современные архитектуры сверточных нейросетей сильно усложнились. Те нейросети, которые побеждали на последних соревнованиях ImageNet — это уже не просто какие-то сверточные слои, Pooling-слои. Это прямо законченные блоки. На рисунке приведены примеры из сети Inception (Google) и ResNet (Microsoft).
По сути, внутри те же самые базовые компоненты: те же самые свертки и пулинги. Просто теперь их больше, они как-то хитро объединены. Плюс сейчас есть прямые связи, которые позволяют вообще не трансформировать изображение, а просто передать его на выход. Это, кстати, помогает тому, что градиенты не затухают. Это дополнительный способ прохода градиента с конца нейросети к началу. Это тоже помогает обучать такие сети.
Это была совсем классика сверточных нейросетей. Да, там есть разные типы слоев, которые можно использовать для классификации. Но есть более интересные применения.
https://arxiv.org/abs/1411.4038
Например, есть такая разновидность сверточных нейросетей, называется Fully-convolutional networks (FCN). Про них редко говорят, но это классная вещь. Можно взять и оторвать последний многослойный персептрон, он не нужен — и выкинуть его. И тогда нейросеть магическим образом может работать на изображениях произвольного размера.
То есть она научилась, допустим, определять 1000 классов в изображениях кошечек, собачек, чего-то еще, а потом мы последний слой взяли и не оторвали, но трансформировали в сверточный слой. Там нет проблем — можно веса пересчитать. Тогда выясняется, что эта нейросеть как бы работает тем же самым окном, на которое она была обучена, 100*100 ps, но теперь она может пробежаться этим окном по всему изображению и построить как бы тепловую карту на выходе — где в этом конкретном изображении находится конкретный класс.
Вы можете построить, например, 1000 этих Heatmap для всех своих классов и потом использовать это для определения места нахождения объекта на картинке.
Это первый пример, когда сверточная нейросеть используется не для классификации, а фактически для генерации изображения.
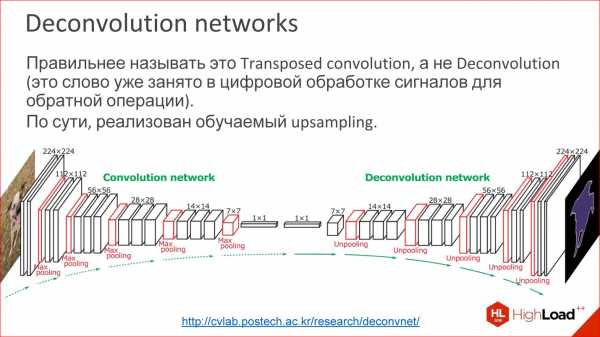
http://cvlab.postech.ac.kr/research/deconvnet/
Более продвинутый пример — Deconvolution networks. Про них тоже редко говорят, но это еще более классная штука.
На самом деле Deconvolution — это неправильный термин. В цифровой обработке сигналов это слово занято совсем другой вещью — похожей, но не такой.
Что это такое? По сути, это обучаемый Upsampling. То есть вы уменьшили в какой-то момент ваше изображение до какого-то небольшого размера, может, даже до 1 ps. Скорее, не до пикселя, а до какого-то небольшого вектора. Потом можно взять этот вектор и раскрыть.
Или, если в какой-то момент получилось изображение 10*10 ps, теперь можно делать Upsampling этого изображения, но каким-то хитрым способом, в котором веса Upsampling также обучаются.
Это — не магия, это работает, и фактически это позволяет обучать нейросети, которые из входной картинки получают какую-то выходную картинку. То есть вы можете подавать образцы входа/выхода, а то, что посередине, обучится само. Это интересно.
На самом деле много задач можно свести к генерации картинок. Классификация — классная задача, но она все-таки не всеобъемлющая. Есть много задач, где надо картинки генерить. Сегментация — это в принципе классическая задача, где надо на выходе картинку иметь.
Более того, если вы научились делать так, то можно сделать еще по-другому, более интересно.
https://arxiv.org/abs/1411.5928
Можно первую часть, например, оторвать, а прикрутить какую-то опять полносвязную сеть, которую обучим — то, что ей на вход подается, например, номер класса: сгенери мне стул под таким-то углом и в таком-то виде. Эти слои генерят дальше какое-то внутреннее представление этого стула, а потом оно разворачивается в картинку.
Этот пример взят из работы, где действительно научили нейросеть генерить разные стулья и другие объекты. Это тоже работает, и это прикольно. Это собрано, в принципе, из тех же базовых блоков, но их по-другому завернули.

https://arxiv.org/abs/1508.06576
Есть неклассические задачи, например, перенос стиля, про который в последний год мы все слышим. Есть куча приложений, которые это умеют. Они работают на примерно таких же технологиях.
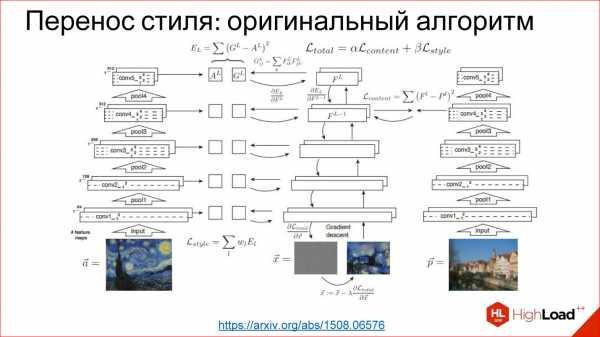
https://arxiv.org/abs/1508.06576
Есть готовая обученная сеть для классификации. Выяснилось, что если взять производную картинку, загрузить в эту нейросеть, то разные сверточные слои будут отвечать за разные вещи. То есть на первых сверточных слоях окажутся стилевые признаки изображения, на последних — контентные признаки изображения, и это можно использовать.
Можно взять картинку за образец стиля, прогнать ее через готовую нейросеть, которую вообще не обучали, снять стилевые признаки, запомнить. Можно взять любую другую картинку, прогнать, взять контентные признаки, запомнить. А потом рандомную картинку (шум) прогнать опять через эту нейросеть, получить признаки на тех же самых слоях, сравнить с теми, которые должны были получить. И у вас есть задача для Backpropagation. По сути, дальше градиентным спуском можно рандомную картинку трансформировать к такой, для которой эти веса на нужных слоях будут такими, как нужно. И вы получили стилизованную карти
habr.com
